6.Расчёт планетарного редуктора.

6.1. Исходные данные.

Передаточное отношение планетарного редуктора-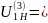

Модуль колёс планетарного редуктора: m₁= мм

Число сателлитов к=3

Угловая скорость водила ω₁=

Число оборотов водила

6.2. Условия проектирования.

П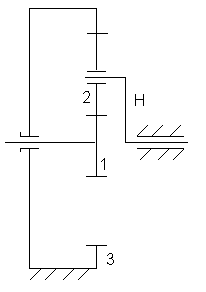 ланетарным называют механизм, составленный из зубчатых колес и вращающихся звеньев, на которых располагаются подвижные оси зубчатых колес. Основным достоинством планетарных механизмов является то, что их масса и габариты значительно меньше массы и габаритов зубчатых механизмов с неподвижными осями, при одинаковых передаточных отношенях и передаваемых моментах.

1.Солнечная шестерня

2.Сателлит.

3.Коронная шестерня

Н- водило

Основные соотношения и условия проектирования:

Формула Виллиса: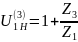

Условие соосности:

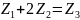
Условие соседства: Рис.6.1.Схема планетарного редуктора.

Условие сборки 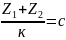, где к- число сателлитов ;с- целое число.

Из условия отсутствия подрезания и заклинивания имеем

Z₁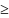 18; Z₂ 20; Z₃ 85

6.3.Подбор чисел зубьев

Проектирование планетарного механизма заключается в определении наименьших чисел зубьев и диаметров начальных(делительных) окружностей, учитывая условия соосности, соседства, собираемости.

1.Передаточное число планетарного редуктора

2.Передаточное число обращенного механизма

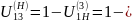
3.Примем Z₁=

4.Число зубьев короной шестерни – Z₃

5.Из условия соосности определяем число зубьев сателлитов Z₂=

6.Из условия соседства определяем максимальное количество сателлитов: 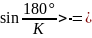при к=4 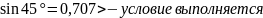при к=3

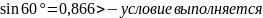
принимаем к=3

7. Проверяем условие собираемости.

8.Фактическое передаточное отношение:

9.Число зубьев планетарного редуктора

Z₁= Z₂= Z₃=

10.Диаметры делительных окружностей, мм

R₁=0,5m₁z₁= R₂=0,5m₁z₂= R₃=0,5m₁z₃=

6.4.Графическое исследование планетарного редуктора

Вычерчиваем кинематическую схему в масштабе в двух проекциях.

Строим план скоростей и план чисел оборотов звеньев в масштабе

где ω=ω₁·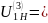

Определяем передаточное число редуктора

а)с помощью плана скоростей

б) с помощью плана чисел оборотов.

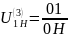
Определяем числа оборотов звеньев планетарного редуктора

обороты кривошипа n=0,1·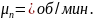

обороты водила n₁= n_н= ОН·

обороты сателлитов n₂=0,2·