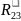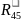5.3.Силовой расчёт группы звеньев 4,5.

5.3.1. Силовой расчёт группы звеньев 4,5.

Изображаем группу звеньев 4, 5 отдельно и прикладываем все действующие на группу силы: , а действия„отброшенных” звеньев заменяем реакциями: .

В соответствии с принципом Даламбера, рассмотрим равновесие плоской произвольной системы сил, действующих на группу. Для определения величины реакции 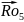составим уравнение равновесия в форме суммы моментов всех сил относительно точки С.

откуда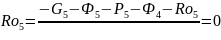 = ;Н

Величины реакции , найдём графическим способом. построив план сил согласно векторному уравнению в масштабе _р=_________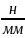

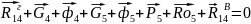
Из плана сил находим:

Давление в кинематической паре 4-5 определяем графически из векторного уравнения равновесия поршня 5.

Для чего соединим начало вектора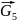 с концом вектора 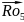, замеряем длину полученного отрезка в мм

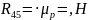
5.3.2. Силовой расчёт группы звеньев 2, 3.

Изображаем расчётную схему нагружения группы и прикладываем силы, действующие на группу: и реакции „отброшеных” звеньев

Для определения величины реакции составляем уравнение равновесия в форме: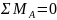

откуда

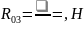
Для определения величины реакции построим план сил, действующих на группу, согласно векторному уравнению в масштабе \

+

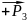Из плана сил находим

Давление в кинематической паре 2-3 определяем из уравнения равновесия сил, приложенных к поршню 3:

+

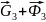5.4.Силовой расчёт кривошипа.

Изображаем схему нагружения ведущего механизма. На ведущее звено АОС действуют:

-реакция шарнира О-

- уравновешивающая сила Р_ур, приложенная в точке А, направляется перпендикулярно звену ОА и создающая уравновешивающий момент

М_ур= Р_ур·ОА.

Уравновешивающую силу определяем из уравнения равновесия кривошипа виде суммы моментов всех сил относительно центра О

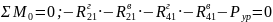
откуда Р_ур=

Р_ур=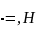

Для определения реакции в шарнире О составляем векторное уравнение равновесия сил, действующих на звено 1.

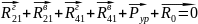
Строим замкнутый многоугольник сил в масштабе 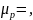из которого следует

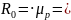,Н

5.5.Определение уравновешивающей силы с помощью „рычага”н.Е. Жуковского.

На плане скоростей в соответствующие точки прикладываем активные силы и силы инерции, повернутые на 90 в одном направлении, уравновешивающую силу прикладываем в точке а перпендикулярно отрезку ра.

Из уравнения равновесия „рычага” (плана сил) в виде силы моменты всех сил. вычисленных относительно полюса плана скоростей Р, найдём величину уравновешивающей силы:

-Ф₅· -Ф₄· -Ф₃· -Ф₂ · -G₄· -G₃· -G₂· -Р₅· -Р₃ -

откуда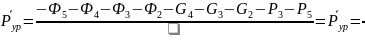 = ,Н

Уравновешивающие моменты.

а) по методу планов сил: М_ур= ·ОА = = ,Нм

б) по „рычагу” Жуковского: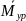 = ·ОА = = ,Нм

Результаты определения давлений в кинематических парах сведём в таблицу5.2.

Величины давлений в кинематических парах, Н Таблица5.2.

Положения механизма										Н·м
										Мур

5.6.Определение мощности двигателя по уравновешивающему моменту. N= М_ур·ω₁= Н·