Задача 4

Функция задана таблицей значений в точках из промежутка :

здесь .

Требуется:

1. представить функцию частичной суммой тригонометрического ряда Фурье, содержащего только синусы или только косинусы; число n нужно подобрать так, чтобы выполнялось неравенство

;

2. найти дискретный амплитудный спектр функции .

Задача 5

Составить представления функции интегралом Фурье. Найти преобразования Фурье и определить непрерывный амплитудный спектр функции .

Решение

1. Построим график заданной функции :

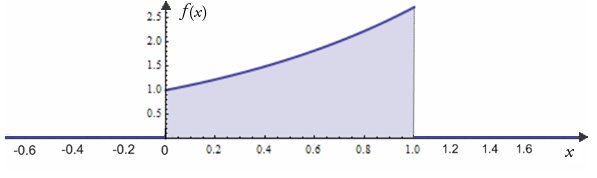
Данная функция f(x) на каждом отрезке [-l,l], где l – любое число, кусочно-монотонная (в нестрогом смысле), кроме того, f(x) – абсолютно интегрируемая функция, т.е. сходится несобственный интеграл . Таким образом, функция может быть представлена интегралом Фурье.

Составим представление функции интегралом Фурье в действительной форме, которое имеет следующий теоретический вид:

где

. (1)

Вычисляем функции :

1) если , то

;

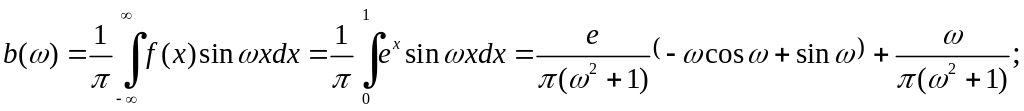
вычисление интегралов проведено методом интегрирования по частям:

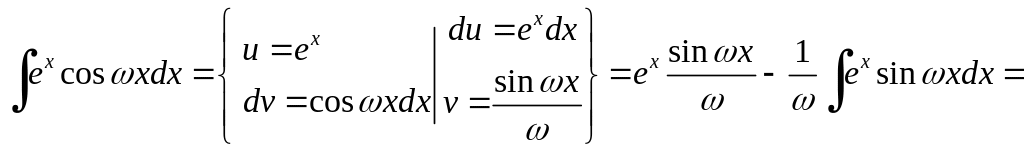
2) если , то

; ;

эти же значения могут быть получены посредством предельного перехода при в предыдущих формулах для :

Подставляя функции в равенство (1), получаем представление данной функции интегралом Фурье в действительной форме:

Составленный несобственный интеграл гарантированно сходится к функции , которая составляется по теореме Дирихле и отличается от функции только в точках скачков;

в решаемой задаче имеет вид:

Комплексная форма интеграла Фурье имеет теоретический вид:

;

вычисляем :

;

подставляя , получаем представление той же функции интегралом Фурье в комплексной форме:

.

2. Чтобы подтвердить достоверность полученного представления функции , построим график интеграла Фурье в действительной форме на промежутке , заменив в несобственном интеграле верхний бесконечный предел интегрирования некоторым большим числом А:

Используем ПП «Wolfram Mathematica 7»:

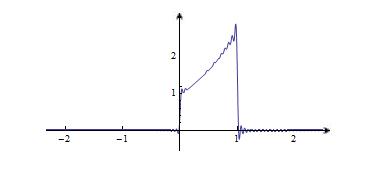
Продолжительность счета при A = 100 примерно 40 минут.

Используем ПП «MathCad»:

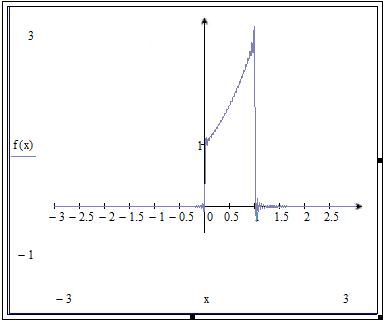
Продолжительность счета при A=150 составляет несколько секунд.

3. Запишем косинус-преобразование Фурье , синус-преобразование Фурье и комплексное преобразование Фурье данной функции :

,

4. Определим непрерывный амплитудный спектр данной функции , построим его график. Для действительной формы интеграла Фурье:

;

график амплитудного спектра по действительной форме интеграла Фурье:

Амплитудный спектр для комплексной формы составленного интеграла Фурье:

= ;

график амплитудного спектра по комплексной форме интеграла Фурье:

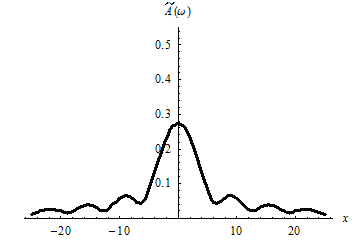
Очевидно, что при выполняется равенство .

Ответ:

1. Представление интегралом Фурье в действительной форме:

представление интегралом Фурье в комплексной форме:

.

2. Преобразования Фурье функции :

(косинус-преобразование);

(синус-преобразование);

, (комплексное преобразование).

3. Амплитудный спектр функции :

, ;

, .