5. Пример выполнения заданий ргз Задача 1

Р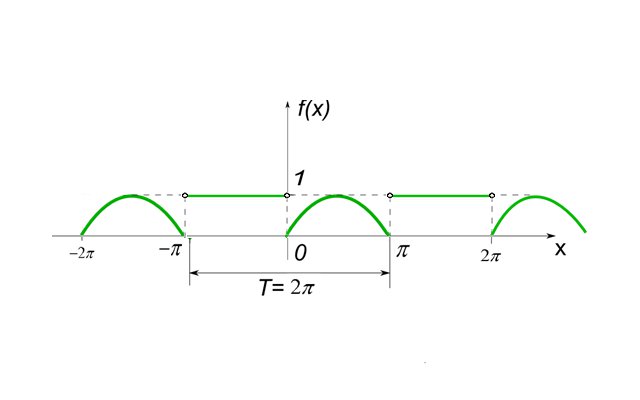 азложить в ряд Фурье периодическую функцию , имеющую наименьший период . Составить сумму ряда .

Решение

1. Построим график функции f(x):

Функция является кусочно-непрерывной (имеет только конечное число точек разрыва первого рода) в каждой точке промежутка , следовательно, удовлетворяет условиям Дирихле, поэтому её можно разлагать в ряд Фурье.

2. Записываем вид ряда Фурье и формулы для его коэффициентов, учитывая, что является -периодической функцией:

;

; ; .

3. Вычисляем коэффициенты Фурье для данной функции :

;

;

;

;

таким образом, для данной функции значения коэффициентов Фурье получились следующими:

Подставляем вычисленные коэффициенты в формально записанный ранее ряд Фурье:

.

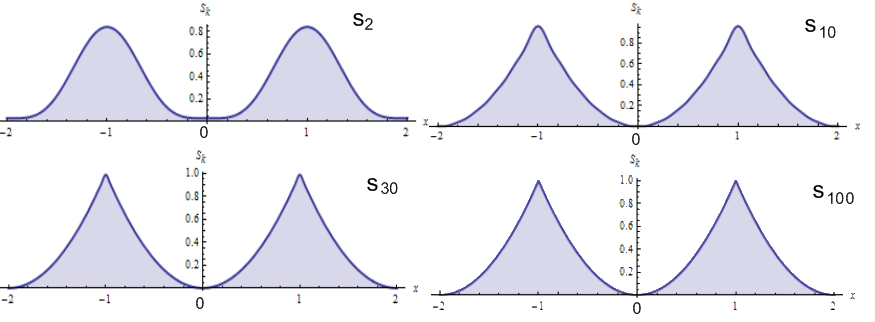
4. Для проверки достоверности разложения построим графики нескольких частичных сумм составленного ряда Фурье:

Используем ПП «Wolfram Mathematica 7»:

Построенные графики частичных сумм показывают, что искомое разложение составлено верно, так как график функции визуально близок к графику функции .

5. Составляем сумму полученного ряда Фурье, используя теорему Дирихле:

Г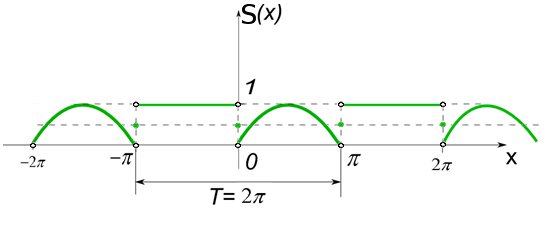 рафик функции :

Ответ: .

Задача 2

Разложить в ряд Фурье функцию , , . Составить сумму ряда .

Решение

1. Построим график исходной функции :

Функция является непрерывной, поэтому удовлетворяет условиям Дирихле, следовательно, может быть представлена рядом Фурье при .

2. Записываем вид соответствующего ряда Фурье для -периодической функции и формулы для его коэффициентов

;

; ; ;

Данная функция является четной, поэтому её коэффициенты Фурье можно вычислить по упрощенным формулам, которые учитывают четность функции :

3. Вычисляем коэффициенты для данной в задаче функции:

;

;

Подставляем посчитанные коэффициенты в записанный формально ряд Фурье:

4. Убедимся в достоверности полученного разложения, построив нескольких частичных сумм составленного ряда:

Используем ПП «Wolfram Mathematica 7»:

5. Сумма ряда совпадает с при , так как f(x) является непрерывной, поэтому В этой задаче график суммы такой же, как и график . В ответ можно записать знак равенства между функцией и её рядом Фурье.

Ответ: .

Задача 3

Составить ряд Фурье в комплексной форме для периодической функции .

Определить дискретный амплитудный спектр функции.

Решение

1. Построим график исходной функции, учитывая её периодичность:

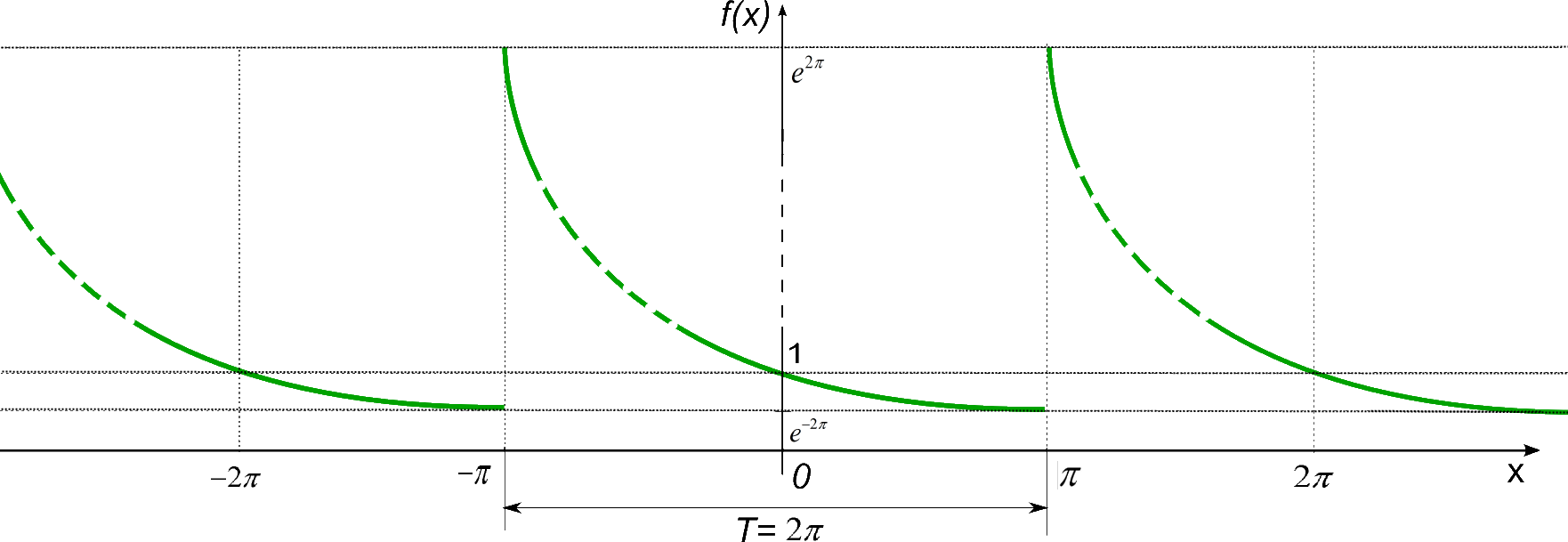
Функция является ограниченной, кусочно-непрерывной, имеет разрывы только первого рода и они образуют счётное множество на всей числовой оси, поэтому эта функция удовлетворяет условиям теоремы Дирихле, следовательно, может быть представлена тригонометрическим рядом Фурье.

Записываем вид этого ряда в комплексной форме и формулы для его коэффициентов:

.

Вычисляем коэффициенты для заданной функции:

.

Подставляем коэффициенты и получаем ряд Фурье в комплексной форме для данной функции:

.

Запишем сумму составленного ряда по теореме Дирихле:

, - периодическая функция с .

2. Чтобы записать полученный ряд Фурье в действительной форме, можно воспользоваться теоретически известными формулами для коэффициентов

,

или выполнить объединение в пары слагаемых комплексного ряда, отличающихся только знаком индекса. В результате выполнения этой работы получим:

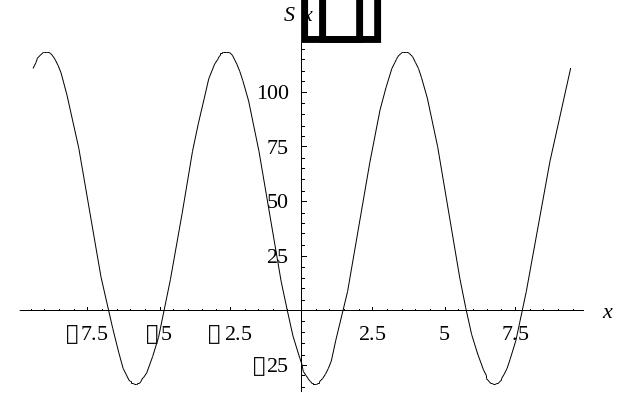
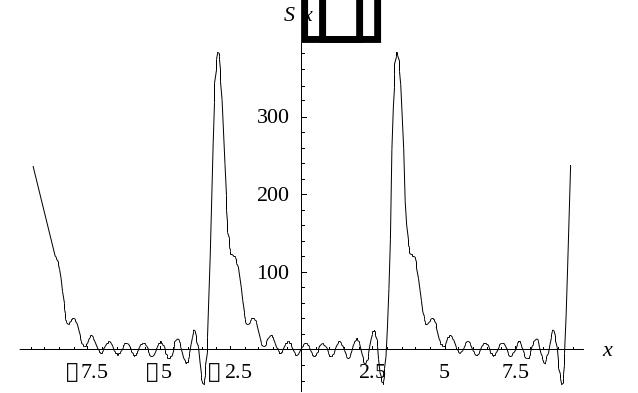
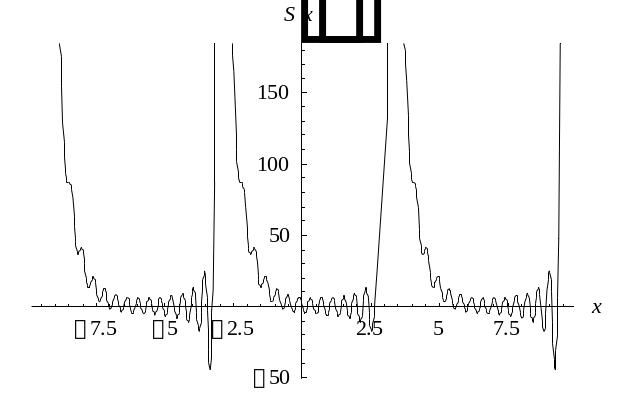
Построим графики частичных сумм ряда Фурье, используя действительную форму этого ряда:

;

будем увеличивать количество членов ряда k до визуального совпадения графика частичной суммы и исходной функции :

		1	2
График
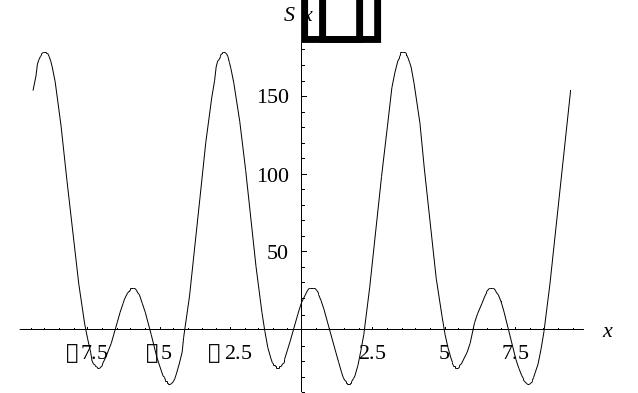
	3		4
График

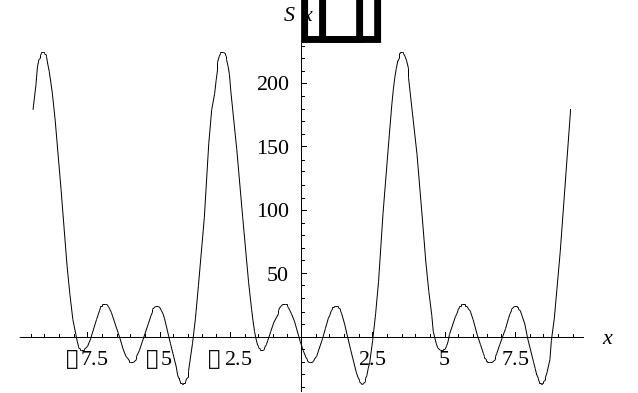
	5	10
График
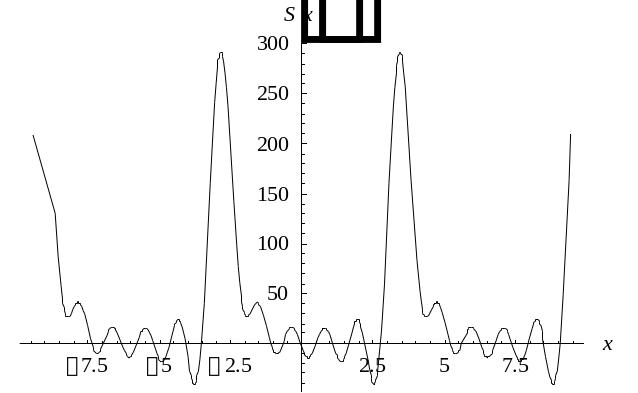
	15	250
График

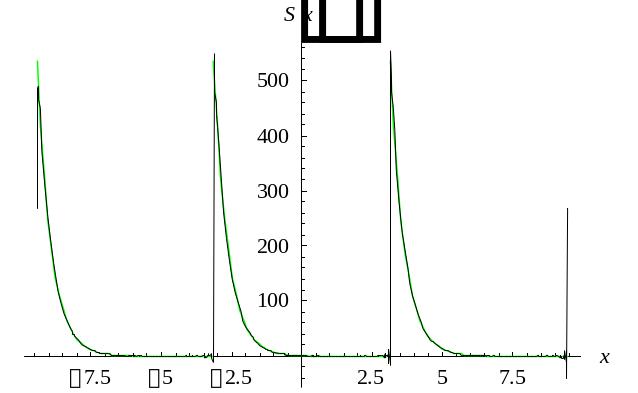
3. Определим дискретный амплитудный спектр заданной функ ции и построим его график:

или

В данной задаче ;

;

очевидно, что

Таблица значений

	1	2	3	4	5	6	7	8
приближ. значение	76.228	60.264	47.274	38.114	31.652	26.950	23.413	20.670
	9	10	11	12	13	14	15	250
приближ. значение	18.488	16.714	15.245	14.011	12.959	12.052	11.264	0.682

Ответ: ; ,