Проверочный расчёт

Производится проверка коэффициента учитывающего потери напряжения от тока холостого хода

где k_i – кратность пускового тока приведённого к обмотке статора при S=1, которая определяется по следующим формулам

Производится проверка синуса угла φ₂

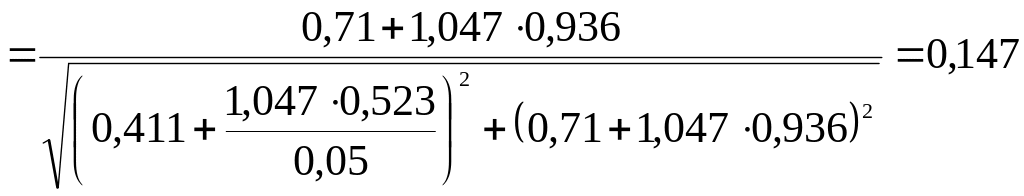
Производится проверка приведённого тока ротора

Производится проверка тока намагничивания

Проверяется величина критического скольжения по формуле

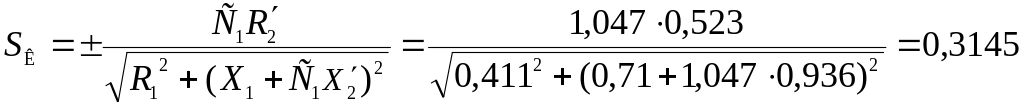
Вывод: Получена удовлетворительная сходимость результатов расчёта. Очевидно, что можно повторить расчёт для уточнения параметров с новыми значениями С₁, sinφ₂ и I΄₂.

Задача №3

Рассчитать и построить естественную механическую характеристику (в масштабе) в двигательном режиме.

Методические указания

В зависимости от числа пар полюсов определяется синхронная частота вращения

(5.30)

Синхронная скорость двигателя

(5.31)

Расчет естественной механической характеристики асинхронного

двигателя произведем в соответствии с выражением (5.6)

При расчёте, задаваясь S, определяется M, данные записываются в таблицу5.6, где также рассчитывается

Таблица 5.6

S, о.е	0,05	0,1	0,2	0,3	0,4	0,5	0,6	0,8	1,0
М, Нм
ω, рад/с

Например для приведённого примера

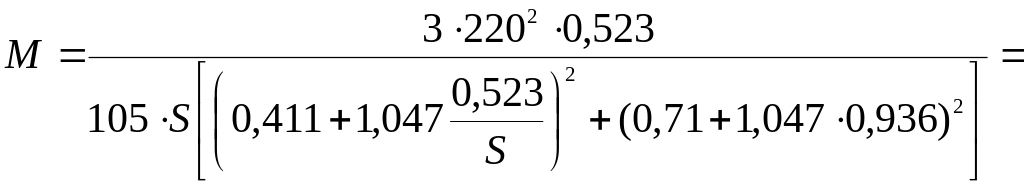
Таблица 5.7

S, о.е	0,05	0,1	0,2	0,3	0,4	0,5	0,6	0,8	1,0
М, Нм	109,8	193,2	283,6	307,23	300,1	282,5	261,7	228,9	191,8
ω, рад/с	99,75	94,5	84.0	73,5	63,0	52,5	42,0	21,0	0,0

Можно также рассчитывать по формуле Клосса

где

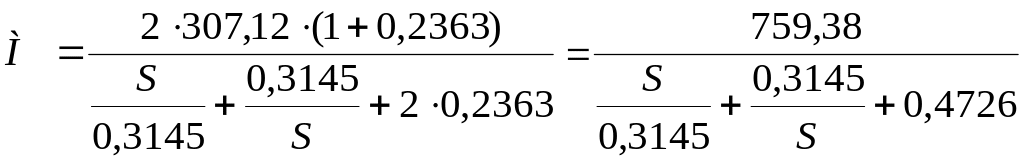
Таблица 5.8

S, о.е	0,05	0,1	0,2	0,3	0,4	0,5	0,6	0,8	1,0
М, Нм	109,7	193,22	283,3	307,44	300.1	282,3	261,0	222,7	191,47
ω, рад/с	99,75	94,5	84.0	73,5	63,0	52,5	42,0	21,0	0,0

Строится естественная характеристика в масштабе (рис. 5.6, кривая 4). Построение характеристики производится на миллиметровой бумаге формата А4 в масштабе, где отмечаются M_Н, M_КД, ω_К, ω_Н.

Определим дополнительные параметры двигателя:

Критический момент двигательного режима

Критическое скольжение (Определено ранее)

Номинальная скорость двигателя

Номинальный момент двигателя

Максимальный момент на валу двигателя

.

Максимальный момент на валу M_К меньше, чем электромагнитный критический момент двигательного режима M_КД, за счёт потерь в самом двигателе.

Задача №4

Рассчитать величины добавочных пусковых сопротивлений графоаналитичским способом и определить скорости при которых производится переключение сопротивлений.

Теоретические положения

Приближённый графический расчёт

Расчет величины добавочного сопротивления ротора двигателя '

R_2Д можно производить по расчетной формуле метода отрезков, записанного для асинхронного двигателя

(5.32)

где R΄₂ – активное фазное сопротивление ротора, приведенное к обмотке статора, Ом.

– скольжение двигателя при моменте M_Сi или M_П на реостатной характеристике, о. е.;

S_e – скольжение, соответствующее моменту M_Сi или M_П на естественной характеристике, о. е..

Для этого строится приближённая пусковая диаграмма, при этом механические характеристики прямыми линиями.

Назначаются: пусковой момент M_П=0,8 M_max и момент переключения M_ПЕР=1,2 M_НОМ, откладывается отрезок aм пропорциональный номинальному скольжению S_Н, проводятся прямые не и нмл, затем строится пусковая диаграмма (рис. 5.7), на основании которой по (5.32) производятся расчеты сопротивлений.

Схема силовых цепей при реостатном пуске асинхронного двигателя приведена на рис. 5.7.

Величина регулировочного сопротивления, непосредственно включаемого в роторную цепь двигателя, находится по формуле

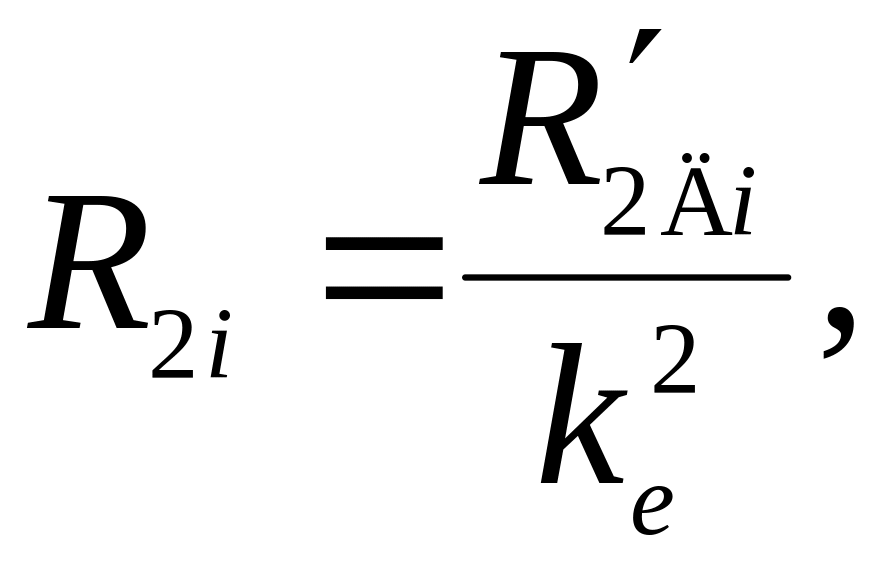(5.33)

где k_е – коэффициент трансформации ЭДС, который можно приближенно определить, зная номинальное линейное напряжение статора

и ЭДС между кольцами неподвижного разомкнутого ротора E_2РН,

k_е=0,95∙U_1ЛН/U_2РН. (5.34)

Величина регулировочного сопротивления, непосредственно включаемого в роторную цепь двигателя, находится по формуле

(5.35)

где k_е – коэффициент трансформации ЭДС, который можно приближенно определить, зная номинальное линейное напряжение статора и ЭДС между кольцами неподвижного разомкнутого ротора E_2РН,

k_е=0,95∙U_1ЛН/U_2РН. (5.36)

Величина регулировочного сопротивления, непосредственно включаемого в роторную цепь двигателя, находится по формуле

(5.37)

где k_е – коэффициент трансформации ЭДС, который можно приближенно определить, зная номинальное линейное напряжение статора и ЭДС между кольцами неподвижного разомкнутого ротора E_2РН

k_е=0,95∙U_1ЛН/U_2РН. (5.38)

Приведённый способ является очень приближённым способом.

Более точный графоаналитический расчёт

Расчет величины добавочного сопротивления ротора асинхронного двигателя R΄_2Д можно произвести аналитически, найдя его из формулы Клосса (5.8)

,

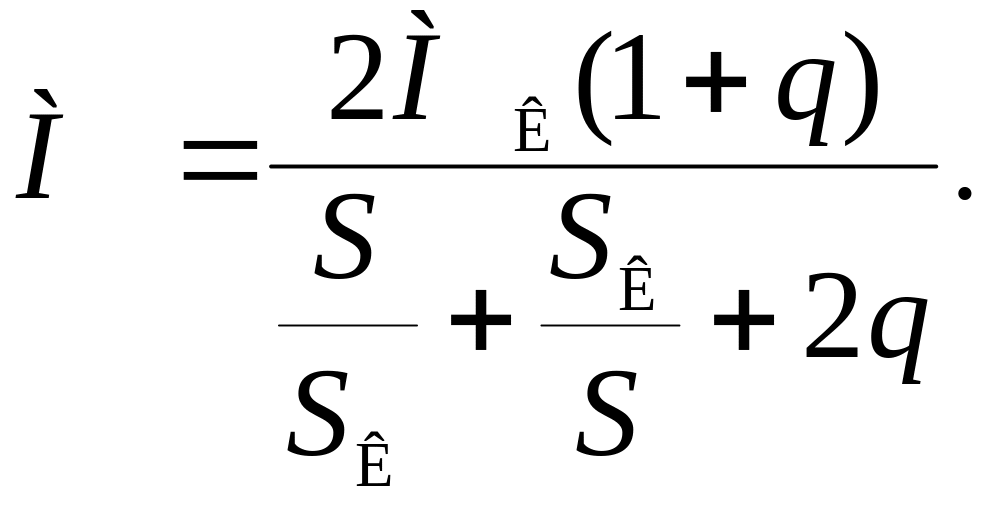
величина коэффициента q не зависит от R΄₂, поэтому, задаваясь координатами M и S можно найти S_К для любой искусственной механической характеристики при различных добавочных сопротивлениях в роторе R΄_2Д.

Решим (5.8) относительно S_К

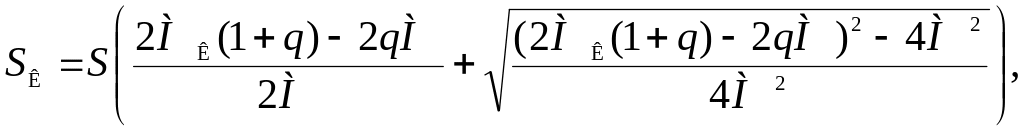
После окончательных преобразований, обозначив: S= S_Иi – скольжение ротора на искусственной реостатной характеристике;

M_Сi – момен сопротивления, соответствующий скольжению ротора S_Иi; - скольжение ротора критическое.

получим

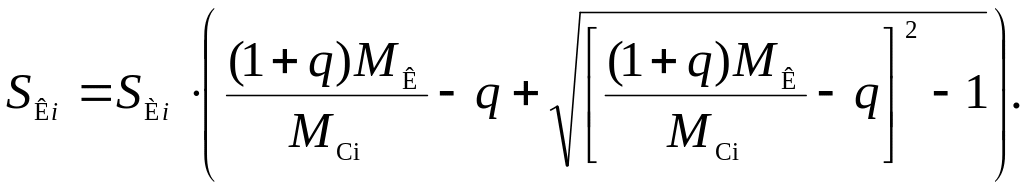(5.39)

Затем найдём добавочное сопротивление при известном S_Кi

(5.40)

Проверка сопротивлений по нагреву выполняется, как правило, после расчета переходных процессов.

С хема силовых цепей при реостатном пуске асинхронного двигателя приведена на рис. 5.8.

Максимальные пусковые пики моментов M_max асинхронных дви-

гателей желательно принимать из условия:

M_max=0,85 M_К. (5.41)

Для двигателей малой мощности допускается принимать пики момента, равные критическому M_К.

Момент переключения M_ПЕР следует выбирать из условия

M_ПЕР=(1,1–1,3).M_Н. (5.42)

Примерный вид механических характеристик при пуске асинхронного двигателя в три ступени пусковых сопротивлений приведен на рис. 5.6.

Порядок построения пусковых характеристик следующий:

Строится естественная или регулировочная характеристика 4. Строится первая пусковая механическая характеристика 1. Характеристика 1 проходит через две точки: синхронная скорость ω₀ при моменте двигателя, равном нулю (M=0), и допустимый момент M_П при скорости, равной нулю (ω=0); определяется момент переключения M_ПЕР , который принимается равным

M_ПЕР=(1,1...1,3) M_Н

в точке с координатами (M_ПЕР , ω_П1 ) происходит закорачивание

первого пускового сопротивления R_С1, и двигатель переходит на пусковую характеристику 2. Таким образом, характеристика 2 проходит через две точки: синхронной скорости ω₀ при моменте двигателя, равном нулю (M=0), и максимальном моменте M_П при скорости, равной ω_П1 .

Закорачивание второго R_С2 и третьего R_С3 пускового сопротив-

ления также необходимо производить при моменте переключения

M_ПЕР . Бросок момента при переходе двигателя на естественную характеристику должен быть равен максимальному моменту M_П .

Если это не происходит, то момент переключения M_ПЕР необходимо поменять, соответственно несколько увеличив или уменьшив его, однако если момент переключения становится меньше 1,1.M_Н , то необходимо увеличить число пусковых сопротивлений.

Конечный график пусковых статических характеристик должен

выглядеть так, как показано на рис. 5.6: в этом случае при заданном

числе пусковых ступеней переходный процесс будет протекать за

меньшее время по сравнению с другими вариантами построения пусковых механических характеристик.

Расчет величин пусковых сопротивлений R΄_2Дi можно произвести

аналитически, в соответствии с уравнениями (5.39), (5.40).

Значение пускового сопротивления R_2Дi , непосредственно включаемого в роторную цепь двигателя, находится по формуле