Методические указания

Расчёт параметров схемы замещения производится на примере двигателя с фазным ротором типа МТН 311–6. Двигатель имеет следующие технические данные:

номинальная мощность P_Н = 11,0 кВт;

номинальное фазное напряжение U_1Н = 220 В;

синхронная частота вращения n₀ =1000 об/мин;

номинальная частота вращения n_Н =950 об/мин;

коэффициент полезного действия электродвигателя в режиме номинальной мощности (100%-я нагрузка) η_Н = 83 %;

коэффициент мощности в режиме номинальной мощности

cosφ_Н=0,79 о. е.;

сопротивление фазы ротора R_Р=0,102 Ом;

кратность пускового момента M_П/M_Н = k_П = 2 о. е.; кратность максимального момента M_max/M_Н = k_max = 2,8 о. е.;

напряжение между кольцами 170 В;

номинальный ток статора 25,4 А;

номинальный ток ротора 43 А.

Решение

Расчёт параметров схемы замещения адкз

Определяется номинальное скольжение

Приближённо задаёмся k_i=6,5, приближённо принимаем

I₀=I_1Нsinφ=25,4∙0,613=15,57

О пределяется коэффициент учитывающий потери напряжения от тока холостого хода

величина этого коэффициента мало отличается от единицы и находится в пределах 1,02…1,06 [6]

Электромагнитная мощность ротора с учётом механических потерь, которые принимаются равными 2% от номинальной мощности

Анализ выражения (5.2) показывает, что за счёт коэффициента С₁ величина тока I΄₂ будет меньше приближённо в С₁ раз.

Синус угла φ₂ на векторной диаграмме равен

Величина синуса этого угла находится в пределах 0,1 – 0,2 и зависит от S_Н. Принимаем в расчетах значение sinφ₂=0,15.

Приведённый ток ротора принимаем, приближённо, равным активной составляющей тока статора с учётом С₁ и sinφ₂=0,15

Определяется приближённое приведённое сопротивление ротора

Тогда С₁R΄₂=1,047∙0,523=0,547 Ом.

Если электродвигатель с фазным ротором и задана величина R₂ в каталожных данных, то определяется коэффициент трансформации от статора к ротору при заторможенном роторе

Определяется сопротивление ротора приведённое к обмотке статора

где α=1,19 – температурный коэффициент при нагреве от 20⁰С до 65⁰С.

Учитывая, что в каталожных данных разных производителей величины R₂ могут отличаться друг от друга, то сравниваются результаты вычислений и принимается величина С₁R΄₂ рассчитанная по формулам, если она отличается от каталожной величины не более чем на 10,0%.

Определяется коэффициент

Расчёт можно производить двумя способами. (Студентам предлагается для проверки проводить расчет обоими способами)

Первый способ.

Из формулы Клосса получена зависимость

Из выражения

найдём зависимость

Задаваясь рядом значений β рассчитываются и строятся графики зависимостей S_К1(β) и S_К2(β) на одном рисунке (см. рис. 5.5).

В точке пересечения будут значения S_К и β удовлетворяющие обоим уравнениям. Расчёты сводятся в таблицы.

Замечание. Анализ выражений S_К1(β) и S_К2(β) показывает, что, если равны отношения чисел в знаменателях и , то графики будут параллельны друг другу, это означает, что величиной R΄₂ задались неверно. Поэтому необходимо вычислить С₁R΄₂ из условия, принимая равенство

Отличие нового значения не должно превышать 20% от принятого ранее. Новая принятая величина является расчётной.

Таблица 5.2

β	0	0,3	1,0	1,3	1,7	2.5
	0,271	0,29	0,332	0,356	0,39	0,5

Таблица 5.3

β	0	0,3	1,0	1,3	1,7	2.5
	0,254	0,275	0,34	0,379	0,588	0,696

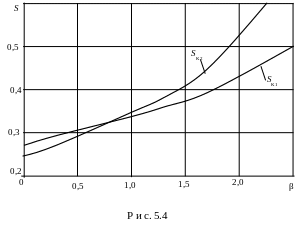
Недостатком первого способа является пересечение кривых под острым углом, что затрудняет принять действительное значение β.

После построения графиков и определения β производится контрольная проверка, величина β должна быть такой величины по графику S_К1(β), чтобы приближённо, в пределах ±10%, при принятом β выполнялось равенство

S_К1≈1,2∙S_К1(0) (5.29)

По условию (5.29) в приближённых расчетах можно принимать с использованием графика величину β.

Второй способ.

Задаёмся значениями S_К1=0,3, S_К2=0,35, S_К3=0,4, S_К4=0,45, S_К5=0,5 в области значений от S_Кmin до 2,5∙S_Кmin, определяемых при β=0, и построим семейство зависимостей по выражению

Таблица 5. 5

β	0	0,3	1,0	1,3	1,7	2.5
(SК1=0,3)	0,646	0,592	0,497	0,465	0,428	0,369
(0,35)	0.753	0,682	0,558	0.518	0,472	0,402
(0,4)	0,861	0,769	0,615	0,566	0,512	0,43
(0,45)	0,97	0,854	0,669	0,61	0,549	0,456
(0,5)	1,076	0.936	0,718	0,652	0,581	0,478

Задаваясь интервалом С₁R΄₂ в пределах ±2,5% от ранее полученной величины по двум графикам можно найти соответствие S_К и β и принять их значения как показано пунктиром на рис. 5.5.

На основании графиков принимаем

Величина критического скольжения на основании формулы Клосса

Проверяется величина активного сопротивления ротора, приведенного к обмотке статора асинхронного двигателя

Полученная величина незначительно отличается от действительного значения, следовательно, величину коэффициента β назначили верно.

Определяется активное сопротивление статора

Определим параметр γ, который позволяет найти индуктивное со-

противление короткого замыкания X_КН

Тогда

X_КН=γС₁R΄₂=3,09∙1,047∙0,523=1,69 Ом.

Индуктивное сопротивление рассеяния фазы роторной обмотки,

приведенное к статорной, может быть рассчитано по уравнению

Индуктивное сопротивление рассеяния фазы статорной обмотки

может быть определено по следующему выражению

X₁=0,42X_КН=0,42∙1,69=0,71 Ом.

По приближённой формуле определяется

Определяется ток намагничивания на основе баланса реактивной мощности

Потребляемая активная мощность на фазу

Полная мощность на фазу

Реактивная мощность на фазу

Определяется сопротивление цепи намагничивания