Расчёт с углом атаки 29.7˚.

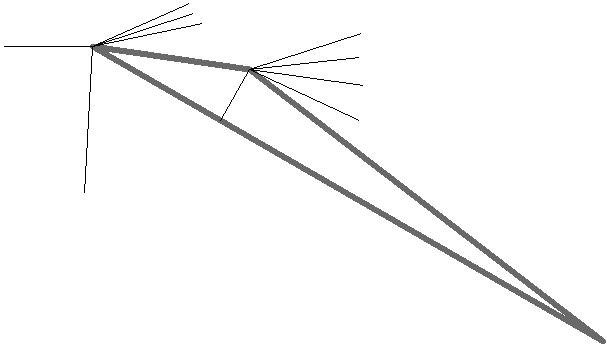
Параметры потока на грани AC находим используя соотношения для косого скачка уплотнения.

AC.

M_AC=1;

Параметры потока на гранях AB и BC находим используя соотношения для течения разряжения

AB. M₁=M_∞=2,5; ω(2.5)=39.12; ; ω(M₂)=46.92

M₂=M_AB=2.857; ;

;

BC. M₁=M_AB= ; ω( )=46.92; ; ω(M₂)=76.32.

M₂=M_BС=4.937;

Определение аэродинамических сил и аэродинамических коэффициентов: Y – подъёмная сила, Х – сила лобового сопротивления, с_х и с_у – аэродинамические коэффициенты этих сил.

α=29.7⁰; ВО=0,1; AO=0.25; OC=0.75; L=1;

р₁=6*10⁴; р₂= ; р₃=3.59*10³;

_{Y1 = p2 * AC – p1 *AO - p3 *OC = 5.624*105;}

_{X1 = p1 * BO– p3 * BO = 2.821*103;}

_{Y = - X1 * sin α + Y1 * cos α = 4.871*105;}

_{X = X1 * cos α + Y1 * sin α = 2.811*105;}

.

c_x=0.634.

; c_y=1.099.

Расчёт с углом атаки 5˚.

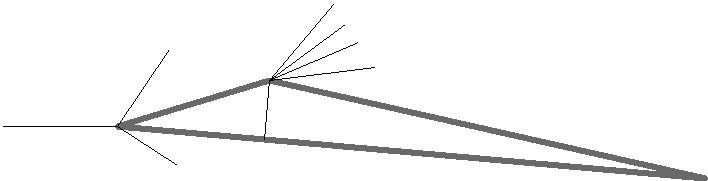
Параметры потока на грани AC, AB находим используя соотношения для косого скачка уплотнения.

AC.

M_AC=2.291;

AB.

M_AB=1.794;

Параметры потока на грани BC находим используя соотношения для течения разряжения.

BC. M₁=M_АB=1.794; ω(1.794)=20.55; ; ω(M₂)=49.95.

M₂=M_BC=3.01;

;

Определение аэродинамических сил и аэродинамических коэффициентов: Y – подъёмная сила, Х – сила лобового сопротивления, с_х и с_у – аэродинамические коэффициенты этих сил.

α=5⁰; ВО=0,1; AO=0.25; OC=0.75; L=1;

р₁=2.76*10⁵; р₂= ; р₃=4.241*10⁴;

_{Y1 = p2 * AC – p1 *AO - p3 *OC = 4.219*104;}

_{X1 = p1 * BO– p3 * BO = 1.168*104;}

_{Y = - X1 * sin α + Y1 * cos α = 4.101 *104;}

_{X = X1 * cos α + Y1 * sin α = 1.531*104;}

.

c_x=0.035.

; c_y=0.093.

Расчёт с углом атаки 0˚.

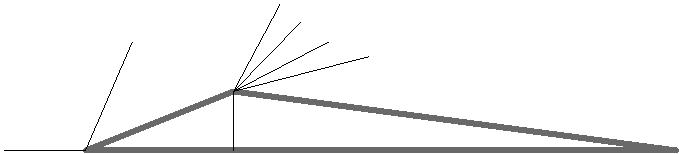
Параметры потока на грани АВ находим используя соотношения для косого скачка уплотнения.

AВ.

;

На грани АС изменений не промсходит:

М_АС =2.5; Р_АС =Р_∞

Параметры потока на гранях BC находим используя соотношения для течения разряжения учитывая разные углы поворота потока.

BC. ;

;

;

;

Определение аэродинамических сил и аэродинамических коэффициентов: Y – подъёмная сила, Х – сила лобового сопротивления, с_х и с_у – аэродинамические коэффициенты этих сил.

α=0⁰; ВО=0,1; AO=0.25; OC=0.75; L=1;

р₁=3.64*10⁵; р₂= ; р₃=6.56*10⁴;

_{Y1 = p2 * AC – p1 *AO - p3 *OC = -3,69*104;}

_{X1 = p1 * BO– p3 * BO = 1.492*104;}

_{Y = - X1 * sin α + Y1 * cos α = -3,69*104;}

_{X = X1 * cos α + Y1 * sin α = 1.492*104;}

.

c_x=0,034.

; c_y=-0,083.

Расчёт с углом атаки -5˚.

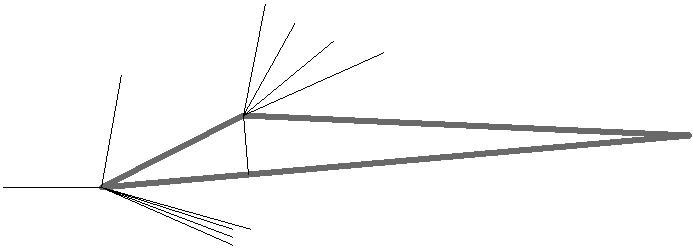
Параметры потока на грани AB, AD находим используя соотношения для косого скачка уплотнения.

AB.

M_AB=1,276;

Параметры потока на гранях AB и BC находим используя соотношения для течения разряжения.

AC. M₁=M_∞=2.5; ω(2.5)=39.12; ; ω(M₂)=44.12.

M₂=M_AC=2.723; ;

;

BC. M₁=M_АB=1.276; ω(1.276)=5.52; ; ω(M₂)=33.92.

M₂=M_BС=2.286; ;

;

Определение аэродинамических сил и аэродинамических коэффициентов: Y – подъёмная сила, Х – сила лобового сопротивления, с_х и с_у – аэродинамические коэффициенты этих сил.

α=-5⁰; ВО=0,1; AO=0.25; OC=0.75; L=1;

р₁=4.71*10⁵; р₂= ; р₃=1.035*10⁵;

_{Y1 = p2 * AC – p1 *AO - p3 *OC = -1.231*105;}

_{X1 = p1 * BO– p3 * BO = 1.838*104;}

_{Y = - X1 * sin α + Y1 * cos α = -1.21*105;}

_{X = X1 * cos α + Y1 * sin α = 2.903*104;}

.

c_x=0.066.

; c_y=-0.273