10.Приближенное нахождение Cy и Cx

= = где = = (104)

Заметим, что определен лишь коэффициент волнового сопротивления . Здесь не рассматривается сила трения, действующая на пластинку со стороны вязкого газа.

Следует добавить, что пластинка является для сверхзвукового потока лучшим крыловым профилем с наибольшим аэродинамическим качеством k = / .

Только соображения необходимой прочности из-за действия поперечных сил вынуждают конструкторов сверхзвуковых летательных аппаратов ставить на них несущие крылья с профилем, утолщающимся в средней части.

При учете только волнового сопротивления формулы (104) являются точными зависимостями для определения коэффициентов и . Для быстрой оценки их значений существуют приближенные формулы Аккерета

= = (105);

для случая малоизогнутых тонких профилей

; (106)

где φ – поправка, учитывающая форму крыла.

- угол атаки

11.Нахождение параметров при обтекании сверхзвукового потока углов профиля

Возможны два случая обтекания потоком углов:

1) Обтекание по внутреннему углу(зона скачков уплотнения) (рис.7)

2) Обтекание по внешнему углу(зона разряжения) (рис.8)

Обтекание по внутреннему углу

1) Из выражений (101) и (86) для косого скачка уплотнения находим

2) Зная значение и из соотношения (83) найдем отношение

3) Зная значение и из соотношения (86) найдем значение Маха за скачком

4) Из формулы находим (98) находим

Обтекание по внешнему углу

1) Зная значение воспользуемся соотношением (52) и найдем

2) Зная угол поворота из соотношения (58) найдем значение

3) Зная воспользуемся соотношением (52) и найдем

4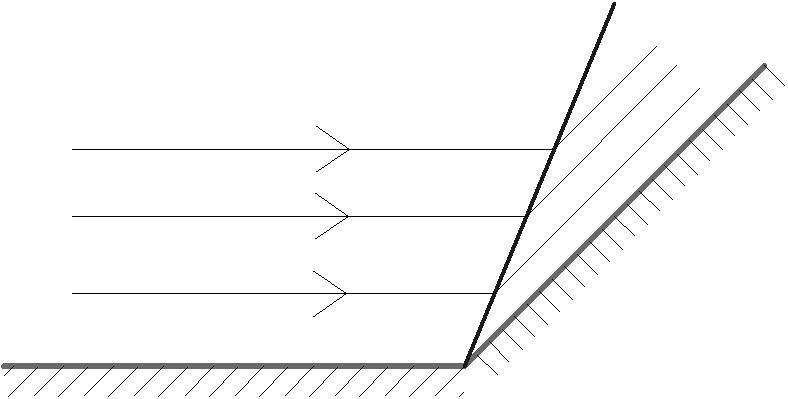 ) Из формулы находим (98) находим P

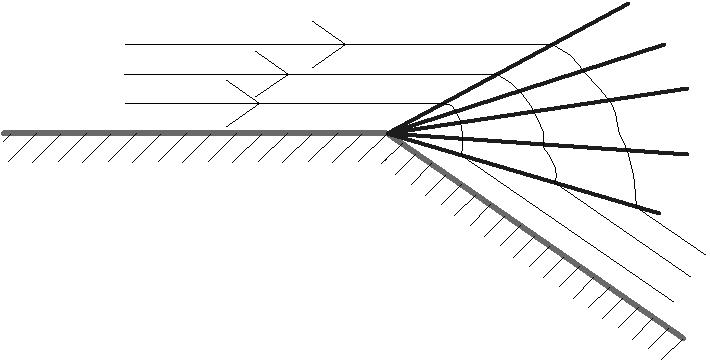рис.7

рис.8

Расчётная часть

Дано:

; ; ; ; ;

Из параметров стандартной атмосферы имеем:

; ; ; ;

; ;

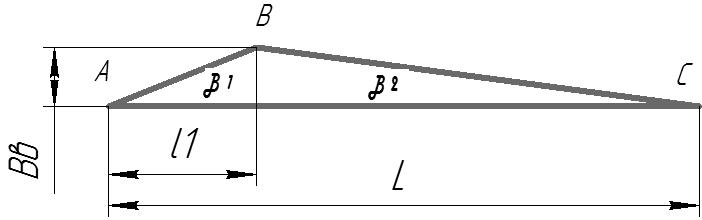
Определение предельных углов атаки для заданного числа маха.

-угол наклона скачка, при котором , определяется из биквадратного уравнения

, где

В выражение для косого скачка

подставим в итоге получим соотношение

Это уравнение достаточно просто решить методом половинного деления, учитывая, что за скачком значение Маха=1, а интервал нахождения от до

Откуда , подставляя в

Максимальное значение угла поворота потока для заданного числа маха: .

Нижний предел: ≥ - _min.

Верхний предел: ≤ _max. -7.9˚≤α≤29.7˚

Для дальнейших расчётов возьмём пять значений углов атаки из данного интервала:

α₁=0˚; α₂=29.7˚; α₃=5˚; α₄=-5˚; α₅=-7.9˚

Формулы для расчёта

(83)

;(86)

следовательно

(52)

; (58)

Используем соотношение статического давления набегающего потока p к давлению торможения

(98)

где давление за скачком уплотнения на грани BС

давление торможения за скачком уплотнения на грани AB

Сначала находим из соотношения

; далее находим из соотношения

, а потом находим