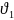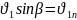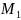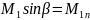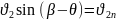- •1.Понятие о методе характеристик
- •2. Характеристические уравнения для установившегося плоского безвихревого сверхзвукового течения газа.
- •3.Уравнение неразрывности в плоской естественной системе координат для установившегося движения.
- •4.Приведение уравнений газодинамики для плоского установившегося безвихревого течения идеального газа к характеристическому виду.
- •5.Определение функции Прандля-Майера
- •6.Течение Прандля-Майера
- •7. Некоторые понятия об ударных волнах.
- •10.Приближенное нахождение Cy и Cx
- •11.Нахождение параметров при обтекании сверхзвукового потока углов профиля
- •Расчётная часть
- •Определение предельных углов атаки для заданного числа маха.
- •Расчёт с углом атаки 29.7˚.
- •Расчёт с углом атаки 5˚.
- •Расчёт с углом атаки 0˚.
- •Расчёт с углом атаки -5˚.
- •Расчёт с углом атаки -7.9˚.
- •Библиографический список:
6.Течение Прандля-Майера
Течение Прандля-Майера называется течение при обтекании равномерным сверхзвуковым потоком выпуклого угла (рис. 4)
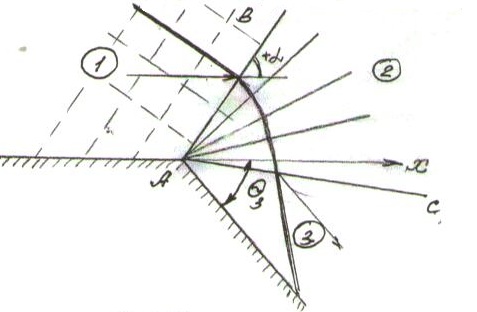
(рис.4)
Заметим, что только
характеристики 2-го семейства проходят
через зоны 1,2,3 одновременно. Следовательно,
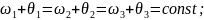 (57)
(57)
Удобно принять
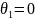 ,
тогда
,
тогда
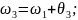 (58),
так как
(58),
так как
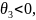 то
то
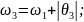 (59)
(59)
Параметры в области
1 заданы и задано значение
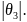 В области 3 параметры постоянны и
находятся в следующей последовательности
В области 3 параметры постоянны и
находятся в следующей последовательности
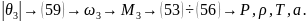
При этом
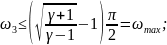 (60). Поэтому, если по формуле (59) получено
(60). Поэтому, если по формуле (59) получено
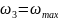 ,
то
,
то
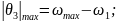 (61).
При
(61).
При
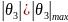 происходит отрыв потока от стенки.
происходит отрыв потока от стенки.
7. Некоторые понятия об ударных волнах.
Ударной волной называют такую поверхность в потоке газа, при переходе через которую параметры газа скачкообразно меняют свои значения: давление, плотность, температура возрастают, а скорость потока уменьшается. Причем изменения эти могут быть очень значительными, так, сверхзвуковой поток может превратиться в дозвуковой.
Основная причина появления ударных волн в сверхзвуковом стационарном течении заключается в том, что информация в этом потоке в виде волн возмущений звуковой интенсивности передается по газу со скоростью, меньшей скорости перемещения самого газа. В качестве примера обтекание равномерным потоком вогнутого угла (рис.5) При дозвуковых скоростях натекающего потока (рис. 5,а) в районе излома стенки создается зона повышенного давления, газовые частицы, приближающиеся к точке излома О, как бы заранее «проинформированы» о том, что предстоит обтекать препятствие в виде отклоненной в сторону потока грани ОВ. Линии тока еще до сближения с наклонной гранью ОВ начинают искривляться, чтобы плавно перейти к новому, параллельному ей направлению. Около самой угловой точки образуется отрывная зона KLO, которая позволяет внешнему (по отношению к газу этой зоны) потоку плавно обтекать область излома стенки. Вообще в дозвуковом потоке линии тока не могут иметь излома. Ситуация принципиально меняется, если перейти к сверхзвуковым скоростям в равномерном натекающем потоке.
а) б)

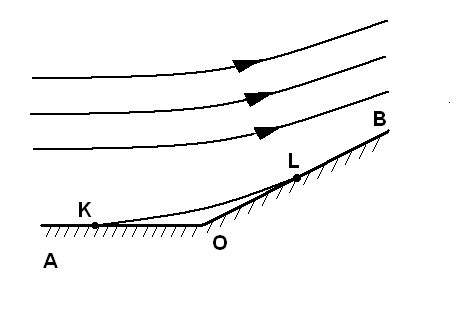
Рис. 5
На рис.4, б геометрически правильно изображена картина обтекания сверхзвуковым потоком с числом Маха M∞=3 двугранного угла с углом излома стенки β=30º. Если в некой точке Е первой грани АО возникают возмущения (небольшая местная неровность стенки), то область их распространения не выходит за линию Маха ED , т.е. характеристику I семейства в натекающем потоке, наклоненную к стенке под углом α∞=arcsin1/M∞ (здесь α∞ = 19,47º) Но вот в точке О поток поджидает уже серьезное препятствие в виде наклоненной к нему грани ОВ, а в отношении информированности потока об этом препятствии здесь наблюдается вообще парадоксальная картина: линия Маха, исходящая из точки О и рассчитанная по параметрам натекающего потока, проходит внутри (!) стенки (линия ОН). Но так как грань ОВ непроницаема для газа и поток около стенки должен идти параллельно ей, то в нем должна возникнуть некая граница ОС, на которой поток «информируется» о наличии наклонной стенки. Более того, от этой прямолинейной границы должен оттекать другой по параметрам поток, параллельный грани ОВ.
Такая картина обтекания сверхзвуковым потоком вогнутого двугранного угла или, что ближе к истине, верхней грани клина, вставленного в поток, действительно имеет место на практике: на линии ОС располагается реальное газодинамическое образование – ударная волна. Некоторая относительно двугранного угла вызвана лишь тем, что в картину обтекания угла вмешивается не рассматриваемый здесь механизм вязкости газа, ведущий к нарастанию пограничного слоя на стенке АО и этим несколько искажающий картину образования ударной волны в окрестности угловой точки.
А теперь немного о структуре ударной волны. В действительности ударная волна имеет определенную толщину, равную нескольким длинам среднего свободного пробега молекул. Но так как длина свободного пробега молекул для газа, находящегося при стандартных условиях, составляет 10-5 см, а характерный размер обтекаемых тел на много порядков больше, то в поле течения ударная волна рассматривается как геометрическая поверхность, не имеющая, как известно, толщины.
На рис. 6 изображена картина обтекания равномерным сверхзвуковым потоком затупленного тела. Перед телом образуется отошедшая ударная волна, которая ни в одной точке не соприкасается с поверхностью обтекаемого тела. Угол наклона волны к набегающему потоку σ непрерывно меняется вдоль волны, и только в одной точке А он прямой, и ударная волна в этой точке называется прямой. В остальных точках, где σ≠90º, ударная волна называется косой. Заметим, что при некоторых условиях и при обтекании заостренных тел образуется такая же искривленная отошедшая ударная волна.
Представим еще один случай возникновения ударной волны. Пусть вдоль прямолинейной стенки АО (рис.6) распространяется равномерный сверхзвуковой поток. В точке О стенка начинает искривляться в сторону потока. Газ, начиная с характеристики OD, тормозится, т.е. в нем падает скорость и растет давление. Причем, следуя выводам п.1.4, можно утверждать, что непосредственно за прямолинейной характеристикой OD все последующие характеристики того же семейства прямолинейны и газодинамические параметры на них постоянны. Поэтому на каждой последующей характеристике давления больше, чем на предыдущей. А так как каждая последующая характеристика имеет и больший угол наклона, то, отходя от стенки, они сгущаются и в конце концов пересекаются. В точке их пересечения возникает конечный скачок давления, иными словами, зарождается ударная волна. Так как эта волна зарождается над стенкой, то её называют висячим скачком (термин «скачок» в стационарных течениях тождествен понятию «ударная волна»).
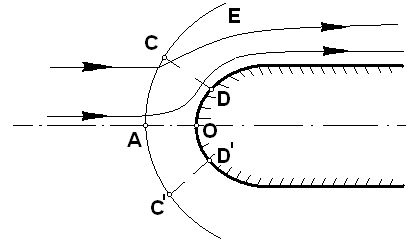
Рис.6
8.Прямой скачок уплотнения
Исходные
соотношения 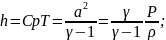 (66)
(66)
Закон
сохранения массы
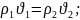 (62)
(62)
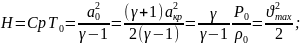 (67)
(67)
Уравнение
движения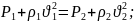 (63)
(63) 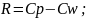 (68)
(68)
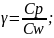 (69)
(69)
Уравнение
энергии
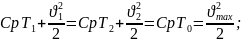 (64)
(64)
Уравнение
термодинамического состояния
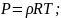 (65)
(65)
8.1.Связь между скоростями
Из
(64) и (66) получаем
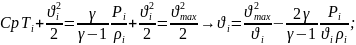 (70)
(70)
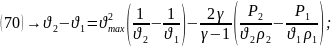 (71)
(71)
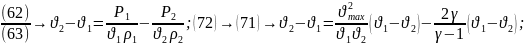 (73)
(73)
т.к.
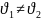 (скачок),
то делим
(скачок),
то делим
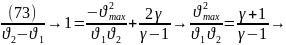
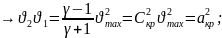 (74),
(74),
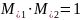 ;(75),
где
;(75),
где
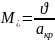 ;
;
2-ое
начало термодинамики
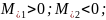
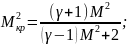 (76)
(76)
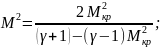 (77)
(77)
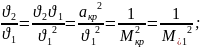 (78)
(78)
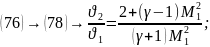 (79)
(79)
8.2.Связь между плотностями
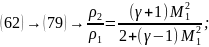 (80)
(80)
8.3.Связь между давлениями
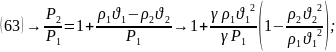 (81)
(81)
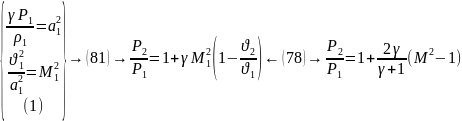
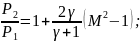 (82)
(82)
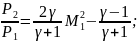 (83)
(83)
8.4.Связь между температурами
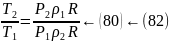 ;
;
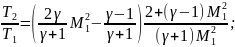 (84)
(84)
8.5.Ударная адиабата
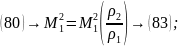
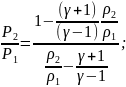 (85)
(85)
8.6.Связь
между числами Маха
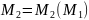
 (86)
(86)
8.7.Изменение энтропии на прямом скачке
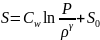
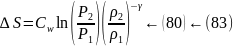
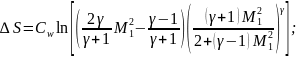 (87)
(87)
В
соответствии со вторым началом
термодинамики
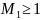
8.8.Потери полного давления на прямом скачке
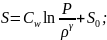 (88)
(88)
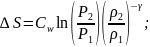 (89)
(89)
Так
как
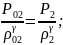 (90),
а
(90),
а
 (91),
(91),
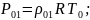 (92),
(92),
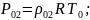 (93),
где
(93),
где
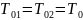 ,
то
,
то
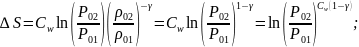 (94),
(94),
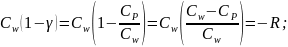
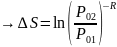 ,
следовательно
,
следовательно
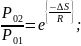 (95)
(95)
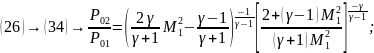 (96)
(96)
8.9.Формула Релея
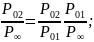 (97)
(97)
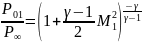 ;(98)
;(98)
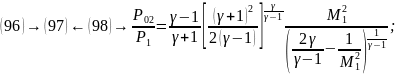 (99)
(99)
9.Косой скачок уплотнения
З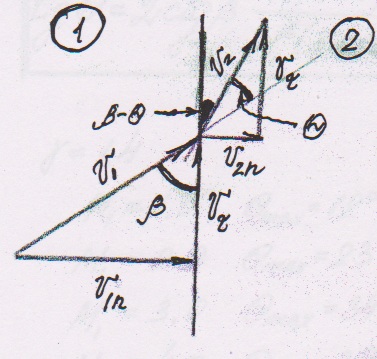 а
основу берем прямой скачок. Накладываем
на него систему координат, двигающуюся
вниз вдоль скачка со скоростью
а
основу берем прямой скачок. Накладываем
на него систему координат, двигающуюся
вниз вдоль скачка со скоростью
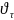 .
Получим картину, изображенную на рисунке.
Следовательно, можно использовать все
соотношения для прямого скачка, если
сделать замену.
.
Получим картину, изображенную на рисунке.
Следовательно, можно использовать все
соотношения для прямого скачка, если
сделать замену.
Прямой скачок |
Косой скачок |
|
|
|
|
|
|
|
|
Определим угол разворота потока на косом скачке
частный случай
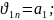
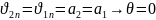
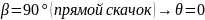
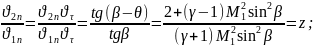
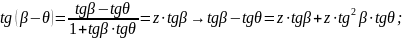
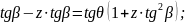
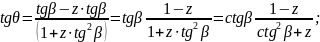
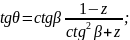 (100)
(100)
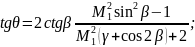 (101)
(101)
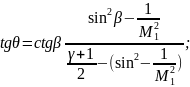 (102)
(102)
Если заданы
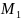 и, кроме того, известны
и, кроме того, известны
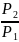 ,
то для определения угла наклона косого
скачка
,
то для определения угла наклона косого
скачка
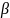 можно получить следующую зависимость.
можно получить следующую зависимость.
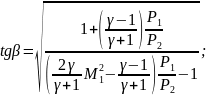 (103)
(103)