4.1. Матрица
4.1.1. Ввод-вывод элементов матрицы
Развитый математический аппарат обработки элементов матрицы определил широкое использование этой структуры данных. В памяти ЭВМ матрицы хранятся по строкам. Соответственно ввод и вывод элементов матрицы в программе осуществляется построчно. Приведем фрагмент программы, осуществляющей построчный ввод элементов матрицы A типа Matr:
type Matr = array[1..5,1..5] of integer; объявлен тип матрицы 5*5 элементов} var A: Matr; {объявлена матрица A целого типа} N, M, I, J: integer; . . . write('Введите количество строк < = 5 '); read(N); write('Введите количество столбцов < = 5 '); read(M); for I := 1 to N do for J := 1 to M do read(A[I,J]); |
При выводе матрицы в программе необходимо предусмотреть смену строки экрана, когда заканчивается каждая строка матрицы, например:
writeln('Вывод матрицы'); for I := 1 to N do begin for J := 1 to M do write(A[I,J]:5);{вывод строки матрицы} writeln;{смена строки экрана} end; |
Если размерность матрицы достаточно велика, то можно осуществить вывод с заданным числом элементов в строке, например:
writeln('Вывод матрицы по 4 элемента в строке'); for I := 1 to N do begin for J := 1 to M do begin write(A[I,J]:7); if J Mod 4 = 0 then writeln; {смена строки после вывода 4-х элементов} end; writeln; {вывод каждой новой строки матрицы с новой строки экрана} end; |
Этот фрагмент выводит элементы каждой строки матрицы следующим образом: 4 элемента по 7 позиций в строке экрана, оставшиеся M-4 элементов - в следующей строке. После чего осуществляется смена строки экрана и вывод очередной строки матрицы.
4.1.2. Определение индексов элементов матрицы
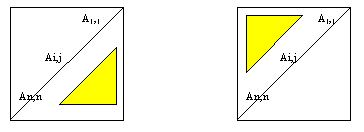
Большое количество задач связано с обработкой части элементов квадратной матрицы (количество строк совпадает с количеством столбцов), например, рассматриваются только элементы главной диагонали, над дополнительной диагональю (соединяющей элементы An,1 и A1,n и т.д. При решении таких задач возникает проблема, определения границ изменения индексов обрабатываемых элементов. Ниже приведем ряд типичных случаев с указанием соответствующих начальных и конечных значений в заголовках циклов.
|
|
элементы, принадлежащие главной диагонали for I:= 1 to N do A[I,I] |
элементы под главной дагональю for I:= 2 to N do for J:= 1 to I-1 do A[I,J] |
|
|
элементы над главной диагональю for I := 1 to N-1 do for J := I+1 to N do A[I,J] |
элементы, принадлежащие диагонали, соединяющей элементы An,1 и A1,n for I := 1 to N do A[I,N+1-I] |
|
|
элементы под диагональю, соединяющей элементы An,1 и A1,n for I := 2 to N do for J:=N-I+2 to N do A[I,J] |
элементы над диагональю, соединяющей элементы An,1 и A1,n for I := 1 to N-1 do for J := 1 to N-1 do A[I,J] |
Приведем фрагмент программы, которая вычисляет произведение элементов квадратной матрицы A[1:K,1:K], принадлежащих главной диагонали и дополнительной диагонали, соединяющей элементы A[K,1] и A[1,K]:
. . . P := 1; for I := 1 to K do P := P * A[I,I] * A[I,K+1-I]; |
Рассмотрим пример вычисления матрицы Y путем замены строк на столбцы в матрице X[1:N,1:N] (задача транспонирования матрицы X):
. . . for I := 1 to N do for J := 1 to M do Y[J,I]:= X[I,J]; writeln('Вывод транспонированной матрицы'); for I := 1 to M do begin for J :=1 to N do write(Y[I,J]:5 ); writeln; end; |
Следующий фрагмент программы осуществляет перемножение двух матриц A[1:N,1:M] и B[1:M,1:L]. Результат размещается в новой матрицы с размерностью N на L. Умножение в соответствии с формулой:
![]()
. . . for I := 1 to N do {цикл по строкам в матрице C} for K := 1 to L do {цикл по столбцам в матрице C} begin S := 0; for J := 1 to M do S := S + A[I,J] * B[J,K]; C[I,K] := S end; |