Расчет на прочность закрытых цилиндрических прямозубых передач

Основным критерием работоспособности закрытых передач является контактная прочность поверхностного слоя зубьев. По этой причине основные размеры передачи определяют из расчета по контактным напряжениям, затем зубья проверяют на изгиб. При выводе расчетной формулы на контактную прочность рассматривают соприкосновение зубьев в полюсе, где происходит однопарное зацепление; при этом контакт зубьев рассматривают как контакт двух цилиндров (рис. 6.31). Расчет ведут по колесу, материал которого менее прочен.

Рис. 6.31. Схема к расчету зубьев на контактную прочность

(1 — эпюра контактных напряжений)

Наибольшее контактное напряжение в зоне зацепления определяют по формуле Герца:

,

где q нормальная на грузка на единицу длины контактной линии зуба; для прямозубых колее длина контактных линий равна ширине обода колеса b₂:

;

К — коэффициент нагрузки (стр. 128), учитывающий неравномерность распределения нагрузки по длине контактных линий и дополнительные динамические нагрузки вследствие погрешностей изготовления и деформации деталей передачи;

Е_пр=2Е₁E₂/(Е₁+E₂) — приведенный модуль упругости,

Е₁ и Е₂— модули упругости материала шестерни и колеса,

ρ_пр=2ρ₁ρ₂/(ρ₁+ρ₂) — приведенный радиус кривизны,

ρ₁ и ρ₂ — радиусы кривизны зубьев шестерни и колеса в полюсе зацепления (см. рис. 6.31).

Из треугольника ВрО₁

ρ₁ = (d₁ sin α)/2=(A sin α)/(1+i).

Из треугольника DрО₂

ρ₂ = (d₂ sin α)/2=(A·i·sin α)/(1+i).

Тогда

ρ_пр =(A·i·sin α)/(1+i)².

Подставив значения q и ρ_пр в формулу Герца, получим

.

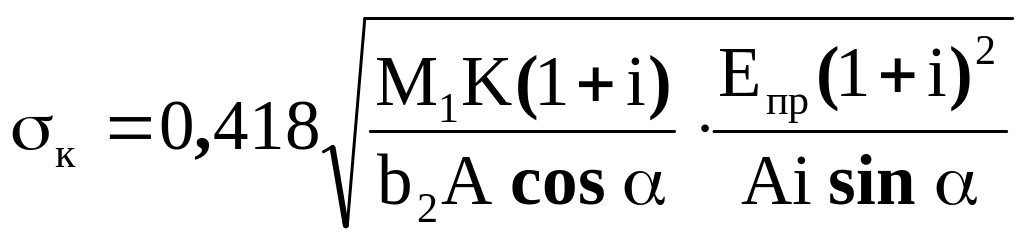Приняв шестерню и колесо стальными с Е_пр=2,1·10⁵ н/мм² и α=20^o, получим формулу проверочного расчета закрытых цилиндрических прямозубых стальных передач:

. (6.39)

Выразив b₂ через А, т. е. b₂=ψ_АА, получим формулу проектного расчета закрытых цилиндрических прямозубых стальных передач:

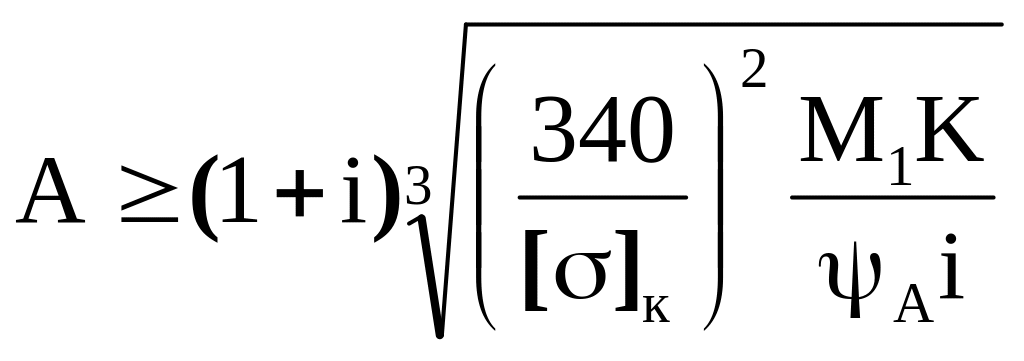, (6.40)

где М₁ — вращающий момент на валу шестерни в н·мм;

[σ]_к — допускаемое контактное напряжение для менее прочного из материалов пары зубчатых колес в н/мм;

ψ_А — коэффициент ширины обода колеса. Для прямозубых передач общего назначения рекомендуется ψ_А=0,2…0,63 (для стандартных редукторов по ГОСТ 2185 — ψ_А =0,1…1,25.) при b₂<=d_д1. При выборе коэффициента ψ_А необходимо учитывать соображения, изложенные при расчете фрикционной передачи.

Численный коэффициент 340 справедлив только для пары стальных, зубчатых колес, причем в нем скрыты определенные единицы измерения. При переходе к другим материалам или к другим единицам измерения численный коэффициент необходимо пересчитать.

Из формул (6.39) и (6.40) следует, что контактная прочность зубьев колес зависит от материала и габаритных размеров передачи и не зависит от модуля и числа зубьев в отдельности. По условиям контактной прочности при данном А модуль зацепления и число зубьев могут иметь различные значения, лишь бы соблюдалось условие m(z₁+z₂)/2=A.

Прочность же зубьев на изгиб, при прочих равных условиях, зависит как от модуля, так и от числа зубьев в отдельности [см. формулу (6.33)].

Проверку поверхности зубьев на предотвращение пластической деформации или хрупкого разрушения от действия кратковременных пиковых нагрузок ведут по [σ]_{к пред}

(6.41)

где σ_{к пик} — расчетное контактное напряжение при перегрузках от М_{1 пик}, действующего на шестерню в период пуска, торможения, буксования и т. д.;

σ_к — расчетное контактное напряжение по формуле (6.39).