Вариант 9
1.Используя метод Крамера, решить системы уравнений:
1)
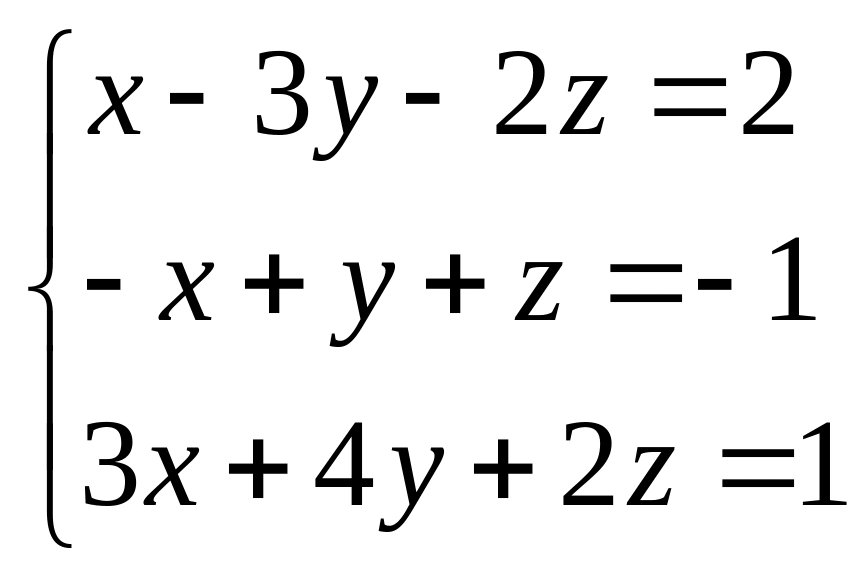2)
.
2.Даны матрицы:
,
,
.
Найти: а) , , , .
б) .
в) матричным методом решение уравнения .
3.Даны вершины пирамиды
.
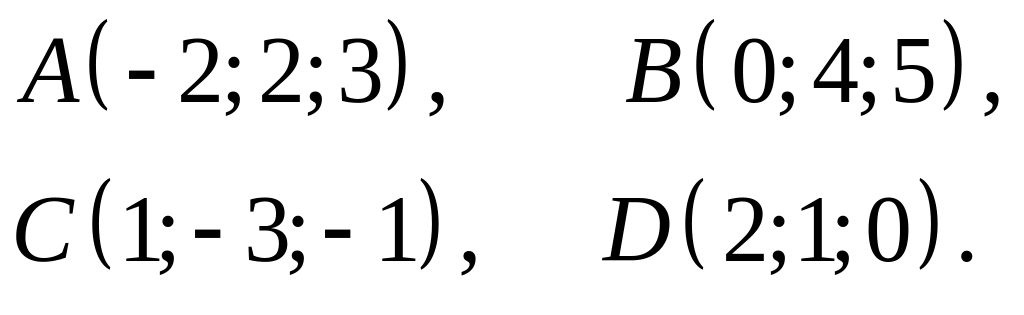б) углы .
Найти: а) длины ребер .
в) площади граней и .
г) объем пирамиды и длину высоты, опущенной из точки А.
4.Дан треугольник на плоскости с вершинами в точках А (-2;3), В(4;5), С(2;-1).
Найти: а) уравнение всех его сторон.
б) уравнение всех высот и всех медиан.
в) точку пересечения высот и точку пересечения медиан.
г) длину одной из высот треугольника.
5.Составить уравнение прямой, проходящей
через точки
6.Через точку
провести прямую, параллельную прямой
.
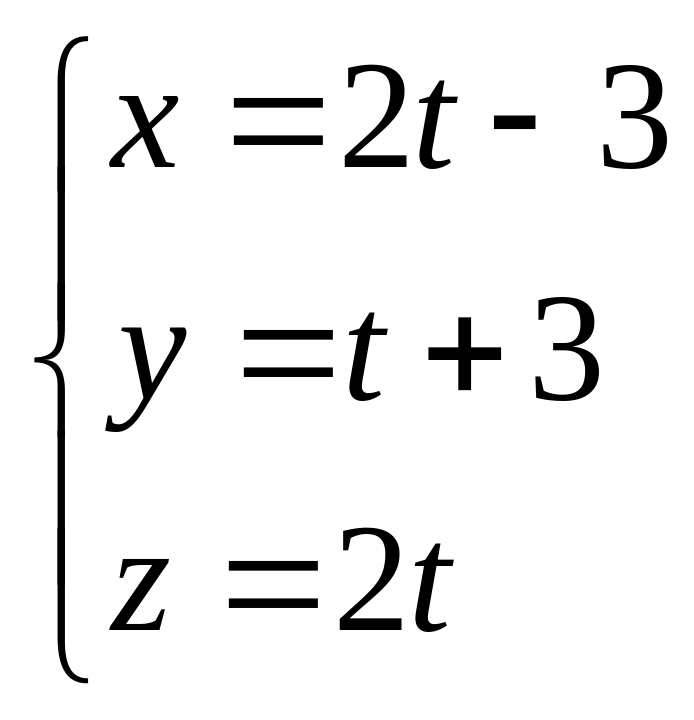7.Составить уравнение плоскости, проходящей через:
а) точки
б) точку
и прямую
.
8.Найти точку пересечения прямой и плоскости:
а)
; 
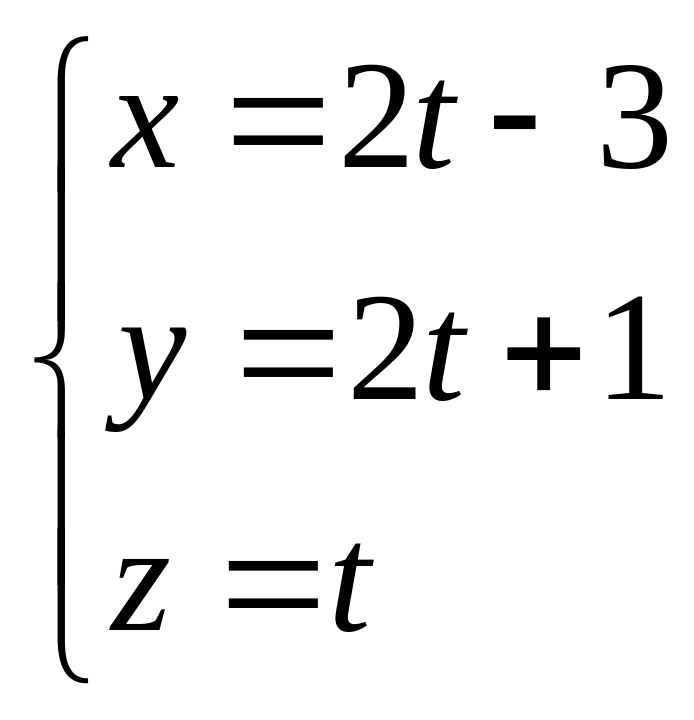9.Найти точку
,
симметричную точке
относительно плоскости
.
10
Вариант 10
1.Используя метод Крамера, решить системы уравнений:
1)
2)
..
2.Даны матрицы:
,
,
.
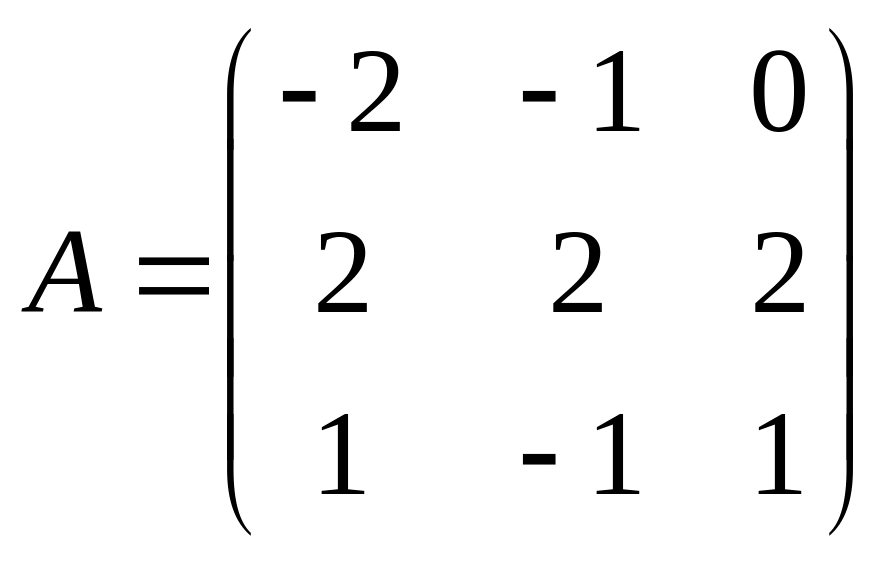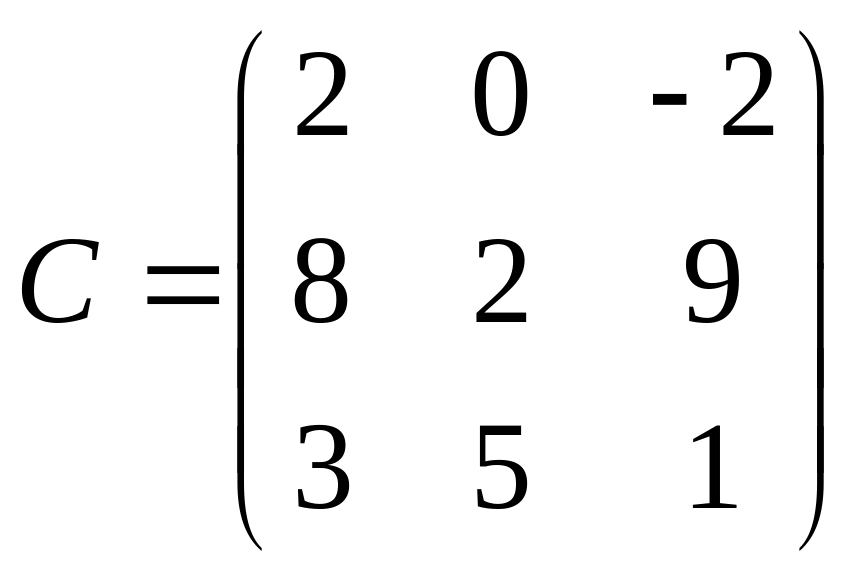Найти: а) , , , .
б) .
в) матричным методом решение уравнения .
3.Даны вершины пирамиды .
б) углы .
Найти: а) длины ребер .
в) площади граней и .
г) объем пирамиды и длину высоты, опущенной из точки А.
4.Дан треугольник на плоскости с вершинами в точках А (-3;2), В(1;0), С(6;-4).
Найти: а) уравнение всех его сторон.
б) уравнение всех высот и всех медиан.
в) точку пересечения высот и точку пересечения медиан.
г) длину одной из высот треугольника.
5.Составить уравнение прямой, проходящей через точки
6.Через точку
провести прямую, параллельную прямой
.
7.Составить уравнение плоскости, проходящей через:
а) точки
б) точку
и прямую
.
8.Найти точку пересечения прямой и плоскости:
а)
; 
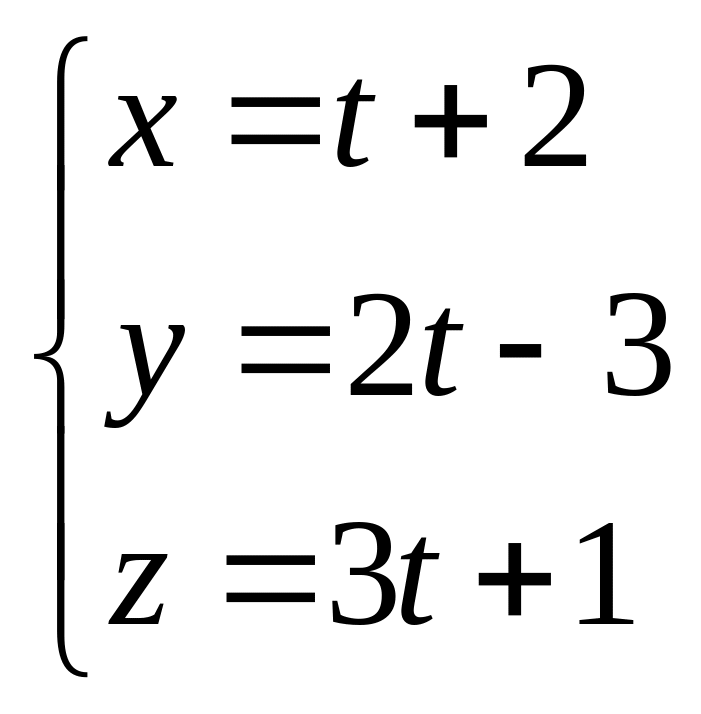9.Найти точку
,
симметричную точке
относительно плоскости
.
Вариант 11
1.Используя метод Крамера, решить системы уравнений:
1)
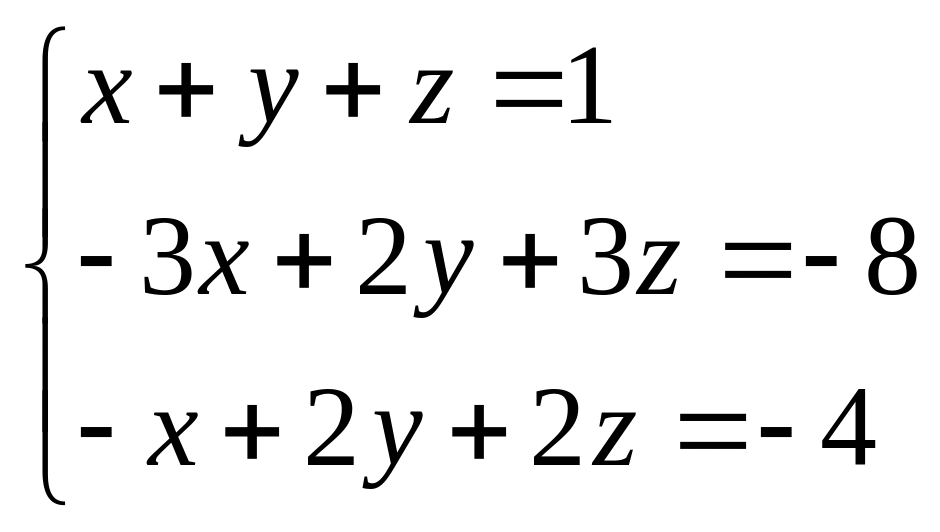2)
.
2.Даны матрицы:
,
,
.
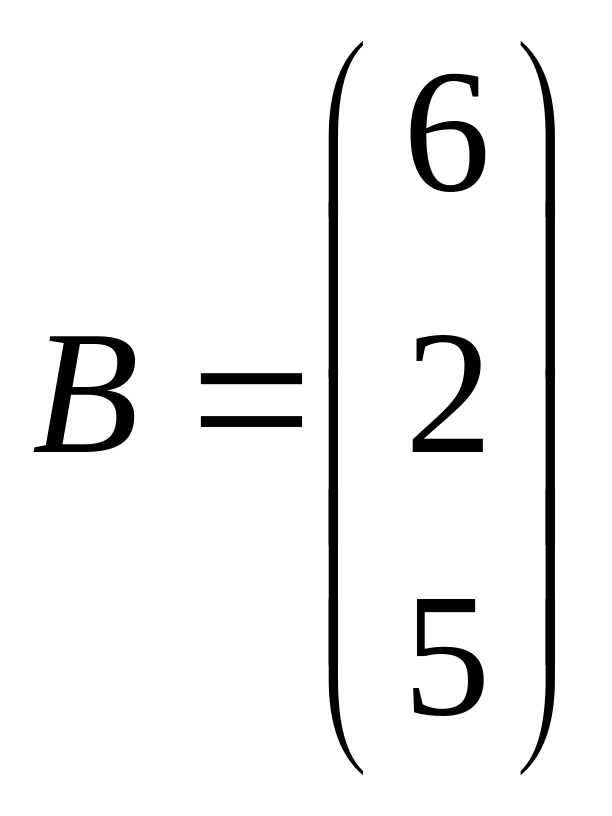Найти: а) , , , .
б) .
в) матричным методом решение уравнения .
3.Даны вершины пирамиды
.
б) углы .
Найти: а) длины ребер .
в) площади граней и .
г) объем пирамиды и длину высоты, опущенной из точки А.
4.Дан треугольник на плоскости с вершинами в точках А (7;1), В(-3;2), С(0;-6).
Найти: а) уравнение всех его сторон.
б) уравнение всех высот и всех медиан.
в) точку пересечения высот и точку пересечения медиан.
г) длину одной из высот треугольника.
5.Составить уравнение прямой, проходящей
через точки
6.Через точку
провести прямую, параллельную прямой
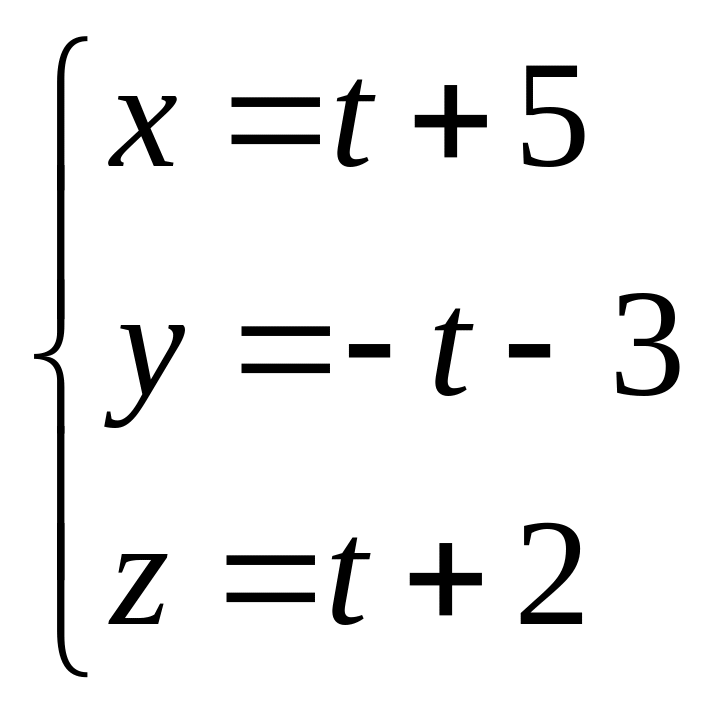
7.Составить уравнение плоскости, проходящей через:
а) точки
б) точку
и прямую
.
8.Найти точку пересечения прямой и плоскости:
а)
; 
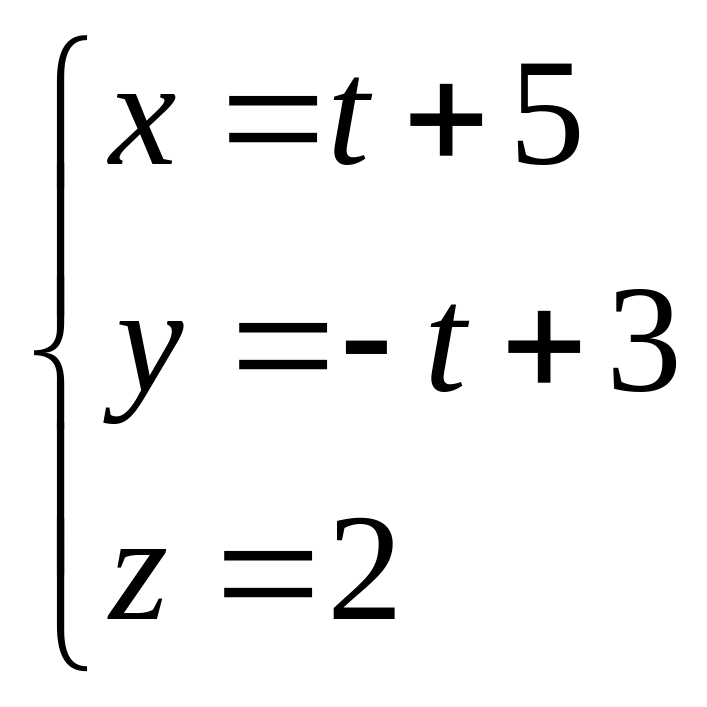9.Найти точку
,
симметричную точке
относительно плоскости
.
Вариант 12
1.Используя метод Крамера, решить системы уравнений:
1)
2)
2.Даны матрицы:
,
,
.
Найти: а) , , , .
б) .
в) матричным методом решение уравнения .
3.Даны вершины пирамиды
.
б) углы .
Найти: а) длины ребер .
в) площади граней и .
г) объем пирамиды и длину высоты, опущенной из точки А.
4.Дан треугольник на плоскости с вершинами в точках А (4;-5), В(3;2), С(-5;0).
Найти: а) уравнение всех его сторон.
б) уравнение всех высот и всех медиан.
в) точку пересечения высот и точку пересечения медиан.
г) длину одной из высот треугольника.
5.Составить уравнение прямой, проходящей
через точки
6.Через точку
провести прямую, параллельную прямой
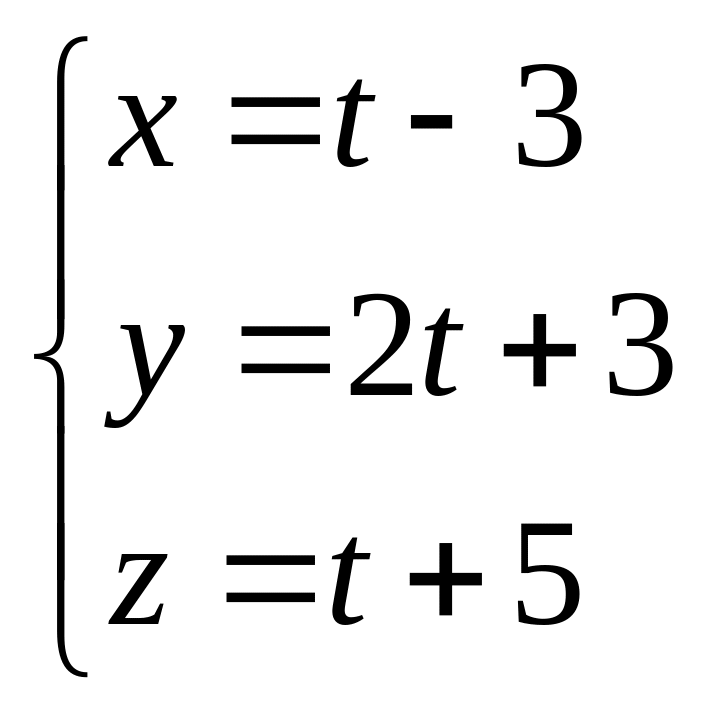
7.Составить уравнение плоскости, проходящей через:
а) точки
б) точку
и прямую
.
8.Найти точку пересечения прямой и плоскости:
а)
; 
9.Найти точку
,
симметричную точке
относительно плоскости
.