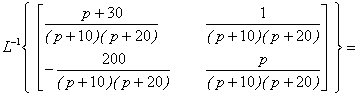- •1. Основные определения теории автоматического управления
- •3. Системы стабилизации, системы программного управления, следящие системы.
- •Знак означает, что управляемая величина поддерживается на заданном уровне с некоторой ошибкой.
- •5. Преобразование Лапласа. Основные свойства преобразования Лапласа
- •4. Дифференциальные уравнения сау. Уравнения статики. Линеаризация уравнений. Стандартная форма записи линейных дифференциальных уравнений.
- •6. Передаточные функции звеньев сау, их связь с дифференциальными уравнениями
- •9. Вещественная и мнимая частотные характеристики сау, их связь с амплитудной и фазовой частотными характеристиками.
- •8. Математическое описание сау в частотной области. Амплитудная и фазовая частотные характеристики сау
- •10. Логарифмические частотные характеристики сау
- •11. Типовые звенья сау
- •12. Интегрирующие и апериодические звенья, их частотные и переходные характеристики
- •13. Дифференцирующие и форсирующие звенья, их частотные и переходные характеристики
- •12. Интегрирующие и апериодические звенья, их частотные и переходные характеристики
- •13. Дифференцирующие и форсирующие звенья, их частотные и переходные характеристики
- •14. Колебательные и консервативные звенья, их частотные и переходные характеристики
- •15) Звено запаздывания, его частотные и переходные характеристики
- •16. Уравнения состояния.
- •17. Основные виды соединений звеньев сау, их передаточные функции, частотные характеристики
- •18. Передаточные функции типовой одноконтурной сау
- •19. Построение частотных характеристик системы по частотным характеристикам звеньев
- •20. Правила построения лах и лфх последовательно соединенных звеньев
- •21. Правила структурных преобразований многоконтурных сау.
- •22. Понятие об устойчивости линейных сау. Необходимое и достаточное условие устойчивости.
- •23. Критерий устойчивости Рауса-Гурвица
- •25. Критерий устойчивости Найквиста. Запасы устойчивости по амплитуде и фазе.
- •26. Логарифмический частотный критерий устойчивости. Определение по лчх запасов устойчивости по амплитуде и фазе.
- •27. Метод д-разбиения построения границ областей устойчивости.
- •28. Оценка качества сау по кривой переходного процесса.
- •29. Оценка качества сау на установившихся режимах. Коэффициенты ошибок. Статические и астатические системы.
- •30. Интегральные оценки качества переходных процессов.
- •31. Способы включения корректирующих устройств.
- •32. Виды обратных связей. Охватывание типовых звеньев жесткой, гибкой и изодромной обратными связями.
- •33. Синтез параметров сау по минимуму интегральной оценки.
- •34. Синтез линейных систем по логарифмическим амплитудно-частотным характеристикам.
- •35. Основные понятия и определения по нелинейным системам.
- •38. Основные виды фазовых траекторий линейных систем второго порядка.
- •39. Основные понятия по Ляпунову об устойчивости нелинейных систем. Основные виды устойчивости нелинейных систем.
- •40. Принципы построения и классификация адаптивных систем.
- •37. Основные методы исследования нелинейных сау. Метод фазовой плоскости.
- •41. Основные виды самонастраивающихся систем. Поисковые и беспоисковые системы.
- •43. Оценка качества переходных процессов по вещественной частотной характеристике замкнутой сау.
- •44. Особенности статистических характеристик соединений нелинейных звеньев.
- •1. Последовательное соединение нелинейных звеньев.
- •2. Параллельное соединение нелинейных звеньев.
- •42. Корневой метод оценки качества управления
- •Диаграмма Вышнеградского
- •45. Прямой метод Ляпунова.
- •46. Методы повышения точности сау.
- •7. Переходная и импульсная переходная характеритстики системы, их связь с передаточной функцией.
15) Звено запаздывания, его частотные и переходные характеристики
Звено
запаздывания входит в состав моделей
многих промышленных объектов управления
. Передаточная функция звена запаздывания
не является дробно-рациональной, что
затрудняет теоретический анализ свойств
системы. Звено запаздывания с хорошей
степенью приближения может быть вынесено
за пределы контура САР. Физический
смысл этого представления состоит в
том, что инерционно-колебательные
свойства и чистое запаздывание контура
разделены и могут рассматриваться
отдельно. Входной сигнал последовательно
преобразуется инерционной частью и
звеном запаздывания. Последовательность
этих процессов может быть произвольной.
Инерционная часть (дробно-рациональная)
формирует фронт переходного процесса,
а звено запаздывания устанавливает
правильную задержку. Линейной системой
с запаздыванием называется такая,
которая содержит в своей структуре
хотябы одно звено, в котором есть
неизменное запаздывание во времени τ
изменения выходной координаты после
начала изменения входной .
Инерционное
звено первого порядка (апериодическое)
- Уравнение
динамики:
Tpy + y = ku.
Передаточная функция: W(p)
=
![]() .
Переходная
характеристика может быть получена с
помощью формулы Хевисайда:
.
Переходная
характеристика может быть получена с
помощью формулы Хевисайда:
![]() Инерционные
звенья второго порядка:Его
уравнение: T12p2y
+ T2py
+ y = ku. Передаточная
функция:
Инерционные
звенья второго порядка:Его
уравнение: T12p2y
+ T2py
+ y = ku. Передаточная
функция:
W(p)
=
![]()
16. Уравнения состояния.
Рассмотрим
методику решения уравнения состояния
линейной стационарной системы,
находящейся в свободном движении. При
этом внешние воздействия на систему
не действуют ( Xвх(t)=
0
) и поведение системы описывается
однородным векторным дифференциальным
уравнением:![]() . Решение
этого уравнения ищем в виде:
. Решение
этого уравнения ищем в виде:![]() , где
Ф(t)
– фундаментальная
матрица;
X(t0)
– вектор, описывающий состояние
системы в начальный момент времени t0
.
, где
Ф(t)
– фундаментальная
матрица;
X(t0)
– вектор, описывающий состояние
системы в начальный момент времени t0
.
Для
стационарных линейных САУ решение
матричного уравнения (6.15) можно получить
по аналогии с решением скалярного
дифференциального уравнения
![]() в
виде:
в
виде:![]() где
где
![]() –
матричная экспонента.
–
матричная экспонента.
Из сравнения выражений (6.16) и (6.17) следует, что фундаментальная матрица равна: Ф(t) = exp(At
Существует несколько способов определения фундаментальной матрицы.
Первый
способ
основан на известном разложении
экспоненты в ряд. Для выражения
(6.18) такое разложение принимает
вид:exp(At)
= 1
+
![]() ,
где 1
– единичная матрица.
,
где 1
– единичная матрица.
Указанный способ определения фундаментальной матрицы обычно используется при численных расчетах для фиксированного момента времени t = t0.
При
этом
exp(At0)
= 1
+ At0
+ A2
![]() +
A3
+
A3![]() +…….
+…….
Вычисление подобного выражения для электронных вычислительных машин является стандартной задачей, не представляющей каких-либо затруднений даже для систем высокого порядка.
Второй способ вычисления фундаментальной матрицы предполагает использование аналитического выражения для Ф(t). Для его определения выполним преобразование Лапласа над обеими частями матричного дифференциального уравнения (6.15):
![]() или
или
![]() ,
,
откуда
Матрица [р1 – А] называется характеристической матрицей, ее определитель det[p1-A] = 0 представляет собой характеристическое уравнение САУ в матричной форме.
Умножая обе части уравнения (6.19) слева на матрицу [р1 – А]-1, обратную по отношению к [р1 – А], получим: X(p) = [р1 – А]-1 X(0).
Выполнив обратное преобразование Лапласа над последним уравнением, имеем X(t) = L-1{[р1 – А]-1} X(0).
Из
последнего выражения следует, что
фундаментальная матрица равна:![]()
В
качестве примера определим фундаментальную
матрицу системы, передаточная функция
которой равна:![]()
Преобразуем
выражение (6.21) к виду:![]() .
.
Используя
метод прямого программирования,
составляем для рассматриваемой системы
схему переменных состояния (рис.
6.7), в качестве которых выбираем выходной
сигнал системы и его первую производную,
т.е.
![]() ,
а
,
а
![]() .
.
Система дифференциальных уравнений для переменных состояния:
![]()
Кроме
того,
![]() .Соответствующие
приведенной системе дифференциальных
уравнений векторные уравнения имеют
вид:
.Соответствующие
приведенной системе дифференциальных
уравнений векторные уравнения имеют
вид:
![]() =
=![]() ;
;
![]()
![]() .
.

![]() Таким
образом, матрицы системы, управления
и наблюдения принимают вид:
Таким
образом, матрицы системы, управления
и наблюдения принимают вид:
A![]() ;
B
;
B
![]() ;
C
;
C
![]() .
.
Характеристическая матрица равна:
![]() .
.
Матрица, обратная характеристической, равна:
![]() .
.
В
соответствии с выражением (6.20)
фундаментальная матрица равна:
=![]()