13. Дифференцирующие и форсирующие звенья, их частотные и переходные характеристики

Дифференцирующим называют звено, которое описывается уравнением , или передаточной функцией .

Уравнение такого звена может быть записано также в виде .

Частотные функции этого звена имеют вид

; ; ; ; ; .

Временные функции этого звена имеют вид

; .

Такое звено физически нереализуемо.

Форсирующее звено. Форсирующим звеном или форсирующим звеном первого порядка называют звено, которое описывается уравнением , или, что тоже, передаточной функцией . Частотные функции этого звена имеют вид

; ; ; ; ; .

Временные функции этого звена имеют вид

; .

Это звено не относится к числу элементарных звеньев. Его можно представить в виде параллельно соединенных дифференцирующего и пропорционального звеньев.

Такое звено физически нереализуемо.

Идеальное интегрирующее

-

Инерционное 1-го порядка (апериодическое)

-

где ; .

Инерционное 2-го порядка (апериодическое)

-

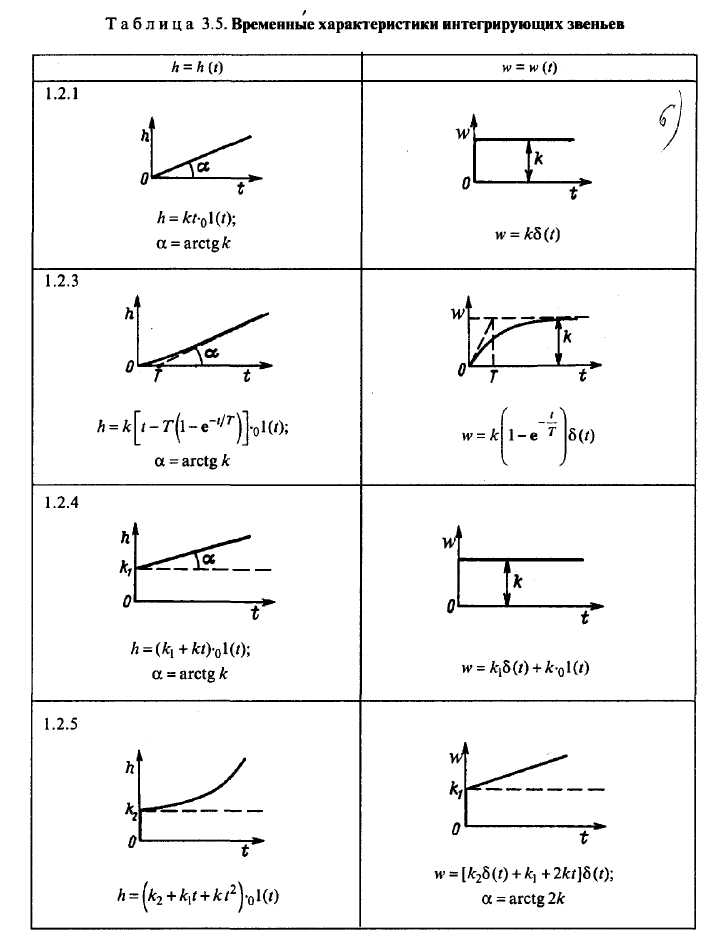
12. Интегрирующие и апериодические звенья, их частотные и переходные характеристики

13. Дифференцирующие и форсирующие звенья, их частотные и переходные характеристики

14. Колебательные и консервативные звенья, их частотные и переходные характеристики

Колебательное звено является элементарным динамическим звеном второго порядка. Колебательное звено описываются достаточно сложные элементы электромеханических систем и электроприводов пример электродвигатель постоянного тока. Передаточная функция колебательного звена: Передаточная функция колебательного звена –

(1)

где – коэффициент усиления, – постоянная времени, – коэффициент затухания. если – звено называют колебательным, так как его временные характеристики носят колебательный характер;

если – звено называют инерционным (апериодическим) звеном второго порядка, так как его временные характеристики носят монотонный характер, то есть колебания отсутствуют;

если – звено называют консервативным, так как его временные характеристики имеют вид незатухающих колебаний, говорят, звено консервирует колебания. Получим временные характеристики колебательного звена. Для этого преобразуем его передаточную функцию (1), вводя обозначения –

– показатель затухания,

– угловая частота колебаний.

W(s) = k w / (wT²(s + λ)²+w²)

импульсную характеристику колебательного звена

– w(t) = ke^{- λ t} sinwt / wT²

переходную характеристику колебательного звена –

h(t) = k( 1- e^{- λ t} ( coswt –( λ/w)sinwt))

Передаточная функция консервативного звена имеет вид –

,

– угловая частота колебаний,

– показатель затухания. частотные характеристики консервативного звена ( ).