Решение системы методом почленного сложения (вычитания) уравнений системы

В ходе решения систем линейных уравнений нужно стараться использовать не «школьный метод», а метод почленного сложения (вычитания) уравнений системы. Почему? Это экономит время и упрощает вычисления, впрочем, сейчас станет всё понятнее.

Пример 4

Решить систему линейных уравнений:

Я взял ту же систему, что и первом примере. Анализируя систему уравнений, замечаем, что коэффициенты при переменной  одинаковы по модулю и противоположны по знаку (–1 и 1). В такой ситуации уравнения можно сложить почленно:

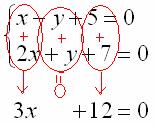
Рассмотрим систему уравнений

На первом шаге вычислим определитель  , его называют главным определителем системы.

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:  и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам: ,

Пример 7

Решить систему линейных уравнений

Решение: Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

, значит, система имеет единственное решение.

;

;

Ответ: ,

Правило Крамера

     Пусть составленный из коэффициентов при неизвестных  определитель:      .      Тогда система (1) имеет единственное решение      ,      где определитель Δ_k  (k=1,2,…n) получен из определителя Δ путем замены k-го столбца столбцом свободных членов системы (1).      Пример. Решить систему линейных уравнений по правилу Крамера:           Решение. Вычислим определители Δ, Δ₁ , Δ₂ , Δ_3.                               Тогда .      Ответ: х₁=1, х₂=0, х₃= -1.

Метод Гаусса

     Метод Гаусса - метод последовательного исключения переменных. С помощью элементарных преобразований строк расширенной матрицы D системы матрицу A системы приводят к ступенчатому виду:

Если среди чисел есть отличные от нуля, система несовместна.

     Если то:

     1) при r = n исходная система равносильна системе:

имеющей единственное решение (сначала находим из последнего уравнения , из предпоследнего и т. д.);