
- •Свойства
- •Войства определителей
- •22) Пусть — матрица размера , и пусть выбраны любые строк матрицы с номерами и любые столбцов с номерами .
- •Разложение определителя по строке (столбцу) (Следствие 1)
- •Следствие 2 (фальшивое разложение определителя)
- •Решение системы методом почленного сложения (вычитания) уравнений системы
Бинарная алгебраическая операция. Группоид. Полугруппа. Группа Пусть А некот орое множество, отображ декартово произвед А*А в А называется бинарн6огйалгебраич операцией или действием на множестве А. из определения=> что бинарная алгебр опер есть бинарное отношение между элементами множеств, которые удов требованию. Каждой паре (а;б)Э А*Асоответсвует единственный элемент СэА. N=2*3=6 (2;3)->Б является алгебраической операцией а,б ЭN (а,б)- а-б 2-3=-1неЭН (3,2)-1 А=(-1,0,1).
х |
-1 |
0 |
1 |
-1 |
1 |
0 |
-1 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
1 |
Таблица Келли задаёт отношение между
декарт произведение множества А. Бинарн
алгебр операция обычно обозн символами
+,*. Вместо записи (а,б)-с, а*б=с.Наука
изучающая алгебраические операции
называется абстрактной алгеброй.
Множество на котором задана одна произв
алгебр операция называется Группоид.
Множество А заданное алгебр операцией
будем оббозн (А;*)Q тетта
из множества А называется нейтральным
элементом, если для каждого Элемента а
из А результат операции а*Q=Q*a=а.
оПР бинарная операция называется
ассоциаьтив если для всех а,б,с из множ
А е\имеет место равенство (а*б)*с=а*(б*с)
ОПР множество в котором бинарное алгебр
операц ассоциативна называется
полугруппой. Группой называется пустое
множество G с алгебраическим
действием *на нём таким, что 1 это действие
ассоциативно,т.е. (G,*)-полугруппа,
2 в G существует нейтральный
элемент тетта, 3 из каждлгл элемента из
G существует симетричный
элемент. Абелева или коммутативная
группа есть группа,
в которой групповая
операция является коммутативной;
то есть группа
![]() абелева
если
абелева
если
![]() для
любых двух элементов
для
любых двух элементов
![]() .
.
Аксиоматическое определение группы. Свойства групп(А*) называется группой, если для элементов множества А выполняются аксиомы А0 замкнутости, А1 ассоциативности, А2 обратимости. 1
 2
2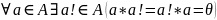 гарантирует существование во множестве
А нейтрального элемента и для каждого
элемента а из А существует симетричный
элемент а! А2!
гарантирует существование во множестве
А нейтрального элемента и для каждого
элемента а из А существует симетричный
элемент а! А2! обратима
справа!
обратима
справа!
Обратима слева (А,*) –абелева группа, если выполняются аксилмы А0,А1.
Кольцо Свойство колец ОПР пусть К множество в котором задано два алгебраических действия, сложение и умножение множество с действием + называется ассоциативным кольцом, если выполняются следующ условия: Сложение ассоциативно, обратимо, коммунитативно , 2 умножение ассоциативно 3 сложение и умножение связано двумя дистрибутивными законами

 , К=(К,+,*)-кольцо- назыывается кольцом,
есмли для элементов множества А. А0
аксиома замкнутости по +
, К=(К,+,*)-кольцо- назыывается кольцом,
есмли для элементов множества А. А0
аксиома замкнутости по + А1 аксиома ассоциативности +
А1 аксиома ассоциативности + А1! Коммуникативности сложения
А1! Коммуникативности сложения
 А2 обратимости сложения
А2 обратимости сложения
 аксиомы щамкнутости умножения теже,
только с * Простейшие свойства кольца
аксиомы щамкнутости умножения теже,
только с * Простейшие свойства кольца
 имеет место 1 а+в=а, в=0, 2 а+в=0, в=-а, 3
–(-а)=а, 4 0*а=а*0=0, 5 (-а)*в=а*(-в)=-(ав),
6(-а)(-в)=ав, 7 (а-в)*с=ас-ав, 8 с(а-в)=са-св.
имеет место 1 а+в=а, в=0, 2 а+в=0, в=-а, 3
–(-а)=а, 4 0*а=а*0=0, 5 (-а)*в=а*(-в)=-(ав),
6(-а)(-в)=ав, 7 (а-в)*с=ас-ав, 8 с(а-в)=са-св.Поле. Свойства полей (Р,+,*) называют полем если для элементов множества Р вып след аксиомы А0 аксиома замкнутости по +
 А1 аксиома ассоциативности +
А1 аксиома ассоциативности + А1! Коммуникативности сложения
А2 обратимости сложения
А1! Коммуникативности сложения
А2 обратимости сложения

 аксиомы
замкнутости умножения теже, только с
* Простейшие свойства кольца
имеет место 1 а+в=а, в=0, 2 а+в=0, в=-а, 3
–(-а)=а, 4 0*а=а*0=0, 5 (-а)*в=а*(-в)=-(ав),
6(-а)(-в)=ав, 7 (а-в)*с=ас-ав, 8 с(а-в)=са-св.
аксиомы
замкнутости умножения теже, только с
* Простейшие свойства кольца
имеет место 1 а+в=а, в=0, 2 а+в=0, в=-а, 3
–(-а)=а, 4 0*а=а*0=0, 5 (-а)*в=а*(-в)=-(ав),
6(-а)(-в)=ав, 7 (а-в)*с=ас-ав, 8 с(а-в)=са-св.Подгруппа. Подмножество H группы G называется подгруппой этой группы, если оно само является группой при той же групповой операции, что и в G. При выяснении того, является ли данное подмножество H подгруппой, можно пользоваться следующей теоремой: Теорема 2. Непустое подмножество H группы G будет подгруппой тогда и только тогда, когда 1) произведение двух любых элементов a и b из H принадлежит H, 2) элемент a -1, обратный для любого элемента a из H, принадлежит к HДоказательство. Необходимость этих условий очевидна. Если, обратно, для H выполнены условия 1) и 2), то H (как непустое множество) содержит элемент a, значит, по свойству 2) оно содержит и a -1 и по свойству 1) aa -1 = e. Таким образом, H содержит единицу e и вместе с любым элементом a содержит обратный элемент a -1. Так как закон ассоциативности автоматически переходит с G на H, то H - подгруппа группы G
Подкольцо. Подмножество M кольца R называется подкольцом, если оно само является кольцом при тех эе операциях сложения и умножения, которые определены в кольце R. Так, кольцо четных чисел является подкольцом кольца целых чисел, а последнее в свою очередь - подкольцом кольца рациональных чисел. При выяснении того, является ли данное множество кольца подкольцом, нет надобности проверять справедливость всех свойств кольца. Большинство из них автоматически переходит с кольца на любое его подмножество. Удобнее всего пользоваться для этого такой теоремой: Теорема 4. Для того чтобы непустое подмножество M кольца R было его подкольцом, необходимо и достаточно, чтобы сумма, разность и произведение любых двух элементов из M снова принадлежали MДоказательство. Для доказательства необходимости этих условий предположим, что M является подкольцом R. Сложение в M совпадает со сложением в R. Но из единственности обратной операции следует, что и вычитание в M совпадает с вычитанием в R. Поэтому сумма, разность и произведение любых двух элементов из M (определенные в кольце R) должны принадлежать снова к M, так как иначе одна из этих операций для данных двух элементов M была бы невыполнима в M, что противоречит определению кольца и следующей из него выполнимости вычитания. Для доказательства достаточности предположим, что множество M удовлетворяет условиям теоремы. Так как сумма и произведение (определенные в R) любых элементов из M снова принадлежат к M, то их можно принять за результат сложения и умножения в M. Этим в M будут определены сложение и умножение. Свойства I, II. IV, V и VI переносятся автоматически с R на любое его подмножество и, значит, выполнены в M. Пусть a и b - элементы M. Тогда b - a = c также есть элемент M. Но по свойству разности в R имеем:a + (b - a) = b или a + c = b.Таким образом, и свойство III выполнено в M, и M является подкольцом кольца R.
Подполе. Простое поле. Множество M поля P называется подполем P, если оно само является полем при тех же операциях сложения и умножения, которые заданы в поле P. Тогда P называется надполем или расширением поля M. Так, поле рациональных чисел является подполем поля действительных чисел, а последнее - подполем поля комплексных чисел.Теорема 5. Для того чтобы множество M поля P, содержащее не менее двух элементов, было подполем, необходимо и достаточно, чтобы сумма, разность, произведение и частное (если только оно существует в P) любых элементов из M снова принадлежали к M. Доказательство вполне аналогично проведенному для соответствующей теоремы о кольцах (теорема 4). Всякое подполе M поля P содержит 0 как разность a - a, где
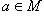 ,
и единицу как частное
,
и единицу как частное
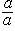 ,
где
,
a ≠ 0. Теорема 6. Пересечение
(в смысле пересечения множеств) любого
множества надполей поля P опять
является подполем поля P. Соответствующая
теорема верна и для колец, т. е. пересечение
любого множества подколец кольца R
есть подкольцо кольца R. Доказательство
ее вполне аналогично данному здесь для
полей.Доказательство. Пусть {Ms}
есть некоторое множество подполей, где
индексы s образуют множество S
и
,
где
,
a ≠ 0. Теорема 6. Пересечение
(в смысле пересечения множеств) любого
множества надполей поля P опять
является подполем поля P. Соответствующая
теорема верна и для колец, т. е. пересечение
любого множества подколец кольца R
есть подкольцо кольца R. Доказательство
ее вполне аналогично данному здесь для
полей.Доказательство. Пусть {Ms}
есть некоторое множество подполей, где
индексы s образуют множество S
и
 -
пересечение всех подполей Ms
данного множества; 0 и 1 входят в каждое
подполе Ms и, значит, в D.
Итак, D содержит не менее двух
элементов. Если a и b - элементы
D, то они входят в каждое Ms
и по теореме 5 a + b, a - b,
ab, а при b ≠ 0 и
также
входят в Ms, а значит, и в
D. В силу теоремы 5 D - подполе
поля P.Поле, не имеющее подполей,
отличных от него самого, называется
простым.Примерами простых полей
могут служить поле рациональных чисел
и поля вычетов по простому модулю
p.Любое подполе M поля P
рациональных чисел содержит число 1, а
значит, и все его кратные n · 1 = n,
т. е. все целые числа, а значит, и все их
частные, т. е. все рациональные числа.
Итак, M = P, т. е. P - простое
поле. Точно так же любое подполе M
поля Cp вычетов по простому
модулю p содержит класс (1), служащий
единицей Cp, а значит, любой
класс (r) как r-кратное класса
(1). Итак, M = Cp, т. е. Cp
- простое поле.Можно доказать, что этими
полями в некотором смысле исчерпываются
все простые поля. Теорема 7. Любое
поле содержит простое подполе и притом
только одно.Доказательство. Поле
P вообще содержит подполя (например,
само P). Пусть D есть пересечение
всех подполей поля P. По теореме 6 D
является подполем P и по самому
определению входит в любое подполе.
Пусть M - подполе D, отличное от
DИз определения подполя следует,
очевидно, что M будет подполем и для
P, и D не входит в M, что
невозможно. Итак, D - простое подполе
P. Если D' - также простое подполе
поля P, то пересечение
-
пересечение всех подполей Ms
данного множества; 0 и 1 входят в каждое
подполе Ms и, значит, в D.
Итак, D содержит не менее двух
элементов. Если a и b - элементы
D, то они входят в каждое Ms
и по теореме 5 a + b, a - b,
ab, а при b ≠ 0 и
также
входят в Ms, а значит, и в
D. В силу теоремы 5 D - подполе
поля P.Поле, не имеющее подполей,
отличных от него самого, называется
простым.Примерами простых полей
могут служить поле рациональных чисел
и поля вычетов по простому модулю
p.Любое подполе M поля P
рациональных чисел содержит число 1, а
значит, и все его кратные n · 1 = n,
т. е. все целые числа, а значит, и все их
частные, т. е. все рациональные числа.
Итак, M = P, т. е. P - простое
поле. Точно так же любое подполе M
поля Cp вычетов по простому
модулю p содержит класс (1), служащий
единицей Cp, а значит, любой
класс (r) как r-кратное класса
(1). Итак, M = Cp, т. е. Cp
- простое поле.Можно доказать, что этими
полями в некотором смысле исчерпываются
все простые поля. Теорема 7. Любое
поле содержит простое подполе и притом
только одно.Доказательство. Поле
P вообще содержит подполя (например,
само P). Пусть D есть пересечение
всех подполей поля P. По теореме 6 D
является подполем P и по самому
определению входит в любое подполе.
Пусть M - подполе D, отличное от
DИз определения подполя следует,
очевидно, что M будет подполем и для
P, и D не входит в M, что
невозможно. Итак, D - простое подполе
P. Если D' - также простое подполе
поля P, то пересечение
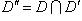 будет
опять подполем поля P, причем
будет
опять подполем поля P, причем
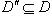 и
и
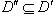 .
Но из определения подполя следует, что
в таком случае D" будет подполем
как для D, так и для D', а так как
D и D' - простые подполя, то D
= D" = D', чем доказана единственность
простого подполя.
.
Но из определения подполя следует, что
в таком случае D" будет подполем
как для D, так и для D', а так как
D и D' - простые подполя, то D
= D" = D', чем доказана единственность
простого подполя.Упорядоченное поле и его свойства Пусть К-поле. Упорядоченное поле К-это подмножество Р в К, обладающее след свойствами . . .
9. Если две алгебраические системы имеют одинаковые алгебраические свойства , то их можно рассматривать как идентичные. Пусть заданы две алгебраические системы
A = hA; f1; f2; : : : ; fk; : : :i и B = hB; g1; g2; : : : ; gk; : : :i с одним и тем же числом алгебраических операций, причјм операции fi и gi с одним и тем
же индексом имеют одинаковую арность ni. Системы A и B называют-
ся изоморфными (запись A ' B), если существует биекция ' : A ! B
такая, что для любого индекса i и любого упорядоченного набора эле-
ментов (a1; a2; : : : ; ani ) 2 Ani выполняется равенство
((a1; a2; : : : ; ani )fi)' = (a1'; a2'; : : : ; ani')gi:
10) Определение.
Отображение
![]() двух
групп G и K
называется изоморфизмом , если
двух
групп G и K
называется изоморфизмом , если
1.Отображение
j взаимно однозначно. 2.Отображение j
сохраняет операцию:
![]() .
.
Пусть
G1 = <Z; +> - аддитивная
группа целых чисел, G2 =
<{5![]() k
| k
k
| k
![]() Z};
+> - аддитивная группа целых чисел,
кратных 5. Отображение
Z};
+> - аддитивная группа целых чисел,
кратных 5. Отображение
![]() (a)
= 5
a
является изоморфизмом группы G1
на группу G2.
(a)
= 5
a
является изоморфизмом группы G1
на группу G2.
12)
Полем комплексных чисел
![]() называется
множество всех упорядоченных пар
действительных чисел
называется
множество всех упорядоченных пар
действительных чисел
![]() .
При этом каждая такая пара
.
При этом каждая такая пара
![]() называется
комплексным числом2).
Таким образом, множество комплексных
чисел можно интерпретировать как точки
на плоскости
называется
комплексным числом2).
Таким образом, множество комплексных
чисел можно интерпретировать как точки
на плоскости
![]() Определим операцию сложения комплексных
чисел по правилу
Определим операцию сложения комплексных
чисел по правилу
![]() для
всех
для
всех
![]() ,
,
и определим операцию умножения:
![]() для
всех
.
для
всех
.
13)
Обозначение. Множество комплексных
чисел принято обозначать
![]() ,
то есть
,
то есть
![]() .
Приняты также следующие обозначения:
.
Приняты также следующие обозначения:
![]() для
для
![]() .
Теорема 2. Каждое комплексное число
.
Теорема 2. Каждое комплексное число
![]() может
быть, и притом единственным образом,
записано в виде:
может
быть, и притом единственным образом,
записано в виде:![]() ,
где
,
где
![]() .
(Такая запись называется алгебраической
формой записи комплексного числа
).Доказательство.
Существуют
такие,
что
.
(Такая запись называется алгебраической
формой записи комплексного числа
).Доказательство.
Существуют
такие,
что
![]() .
Имеем
.
Имеем![]() .
Теорема 3. Число
.
Теорема 3. Число
![]() обладает
свойством:
обладает
свойством:
![]() .Доказательство.
.Доказательство.
![]() .
Из равенства
следует,
что
.
Из равенства
следует,
что
![]() Определение.
Пусть
,
где
.
Число
Определение.
Пусть
,
где
.
Число
![]() называется
действительной частью,
называется
действительной частью,
![]() -
мнимой частью комплексного числа
.
Пишем
-
мнимой частью комплексного числа
.
Пишем
![]() .
Пусть
-
алгебраическая форма записи комплексного
числа
.
Тогда:если
.
Пусть
-
алгебраическая форма записи комплексного
числа
.
Тогда:если
![]() ,
то
,
то
![]() ;если
;если
![]() ,
то
,
то
![]() .Определение.
Если
.Определение.
Если
![]() ,
то комплексное число
называют
чисто мнимым числом.Действия над
комплексными числами в алгебраической
форме1) Для
,
то комплексное число
называют
чисто мнимым числом.Действия над
комплексными числами в алгебраической
форме1) Для
![]()
![]() .Другими
словами: комплексное число равно нулю
тогда и только тогда, когда у него
действительная и мнимая части равны
нулю.Доказательство.
.Другими
словами: комплексное число равно нулю
тогда и только тогда, когда у него
действительная и мнимая части равны
нулю.Доказательство.
![]() .
2) Для
.
2) Для
![]()
![]() .Другими
словами: два комплексных числа равны
тогда и только тогда, когда у них,
соответственно, равны действительная
и мнимая части.Доказательство.
.Другими
словами: два комплексных числа равны
тогда и только тогда, когда у них,
соответственно, равны действительная
и мнимая части.Доказательство.
![]() .
3) Для
.
3) Для
![]() .Другими
словами: чтобы сложить два комплексных
числа, нужно, соответственно, сложить
их действительные и мнимые
части.Доказательство.
.Другими
словами: чтобы сложить два комплексных
числа, нужно, соответственно, сложить
их действительные и мнимые
части.Доказательство.
![]()
![]() .
4) Для
.
4) Для
![]() .Доказательство.
.Доказательство.
![]()
![]() .
5) Для
.
5) Для
![]() .Доказательство.
.Доказательство.
![]() .
6) Для
,
если
.
6) Для
,
если
![]() ,
то
,
то
![]() .Доказательство.
.Доказательство.
![]()
![]() .
.
14)
Геометрическая интерпретация комплексных
чисел.Пусть
записано
в алгебраической форме
.
Поставим в соответствие числу
точку
плоскости с координатами
![]() .
Это соответствие является биекцией
множества комплексных чисел на множество
точек плоскости. Проиллюстрируем это
соответствие Рис.1. В дальнейшем мы будем
считать, что точками плоскости являются
комплексные числа и будем называть эту
плоскость комплексной плоскостью.Числа
и
.
Это соответствие является биекцией
множества комплексных чисел на множество
точек плоскости. Проиллюстрируем это
соответствие Рис.1. В дальнейшем мы будем
считать, что точками плоскости являются
комплексные числа и будем называть эту
плоскость комплексной плоскостью.Числа
и
![]() расположены
симметрично относительно оси абсцисс.
Действительные числа расположены на
оси абсцисс, поэтому ось абсцисс - ось
действительных чисел. На оси ординат
расположены числа, у которых действительная
часть равна нулю. Иногда ось ординат
называют осью мнимых чисел.
Тригонометрическая форма записи
комплексного числа. Аргументом
комплексного числа
называется
число
расположены
симметрично относительно оси абсцисс.
Действительные числа расположены на
оси абсцисс, поэтому ось абсцисс - ось
действительных чисел. На оси ординат
расположены числа, у которых действительная
часть равна нулю. Иногда ось ординат
называют осью мнимых чисел.
Тригонометрическая форма записи
комплексного числа. Аргументом
комплексного числа
называется
число
![]() ,
равное величине угла между положительным
направлением оси абсцисс и вектором
,
определяется
с точность до углов, кратных
,
равное величине угла между положительным
направлением оси абсцисс и вектором
,
определяется
с точность до углов, кратных
![]() .
Главным значением аргумента комплексного
числа
называется
то значение
,
которое принадлежит промежутку
.
Главным значением аргумента комплексного
числа
называется
то значение
,
которое принадлежит промежутку
![]() ,
оно обозначается
,
оно обозначается
![]() и
и
![]() .
Пусть
записано
в алгебраической форме
.
Пусть
записано
в алгебраической форме
![]() .
Тогда из геометрической интерпретации
следует,
что:
.
Тогда из геометрической интерпретации
следует,
что:![]() ;
;![]() ,
если
,
если
![]() ;
;![]() ,
если
,
если
![]() ;
;![]() ,
если
,
если
![]() .Заметим,
что
выражается
только в радианах,
.Заметим,
что
выражается
только в радианах,
![]() не
определён.
не
определён.
Записать
число
![]() в
тригонометрической форме.
в
тригонометрической форме.
Найдём
модуль этого числа:
Значит,
один из аргументов числа
равен
Ответ. |
15)
Найти произведение комплексных чисел
![]() ,
,
![]()
Очевидно,
что произведение следует записать
так:
![]()
![]() Даны
комплексные числа
Даны
комплексные числа
![]() ,
,
![]() .
Найти частное
.
Найти частное
![]() .
.
Составим частное:

![]() формула Муавра: Если комплексное
число представлено в тригонометрической
форме
формула Муавра: Если комплексное
число представлено в тригонометрической
форме
![]() ,
то при его возведении в натуральную
степень
,
то при его возведении в натуральную
степень
![]() справедлива
формула:
справедлива
формула:
![]()
16) Корни из комплексных чисел.
Определение.
Пусть
![]() ,
,
![]() .
Комплексное число
.
Комплексное число
![]() называется
корнем степени
называется
корнем степени
![]() из
из
![]() ,
если
,
если
![]() .
.
Теорема
6. Пусть
,
![]() -
множество всех корней степени
из
1. Тогда алгебра
-
множество всех корней степени
из
1. Тогда алгебра
![]() -
группа, (которая называется группой
корней степени
из
1).
-
группа, (которая называется группой
корней степени
из
1).
Доказательство.
Пусть
![]() .
.
Проверим,
что умножение – бинарная операция.
Имеем
![]() -
корень степени
-
корень степени
![]() из
1.
из
1.
Проверим,
что
![]() -
унарная операция. Имеем
-
унарная операция. Имеем
![]() -
корень степени
из
1.
-
корень степени
из
1.
Очевидно, что 1 – корень степени из 1.
Доказано,
что
![]() -
алгебра.
-
алгебра.
То, что алгебра - группа, следует из свойств комплексных чисел.
17)
Решение двучленного уравнения четвертой
степени.Этот тип уравнений четвертой
степени является простейшим, само
уравнение имеет вид
![]() Решается
с использованием формул сокращенного
умножения.
Решается
с использованием формул сокращенного
умножения.
 И
находятся корни двух полученных
квадратных трехчленов.Решить уравнение
четвертой степени
И
находятся корни двух полученных
квадратных трехчленов.Решить уравнение
четвертой степени
![]() РешениеРазложим
на множители многочлен
РешениеРазложим
на множители многочлен
![]()
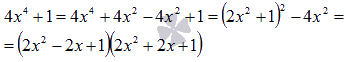

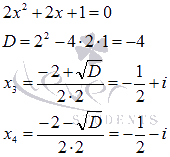 Ответ:
Ответ:
![]() или
или
![]()
Решение
возвратного уравнения четвертой
степени.Уравнение вида
![]() называют
возвратным уравнением четвертого
порядка.Легко проверить, что х=0 не
является корнем этого уравнения:
называют
возвратным уравнением четвертого
порядка.Легко проверить, что х=0 не
является корнем этого уравнения:
![]() .
Поэтому можно разделить на
.
Поэтому можно разделить на
![]() обе
части уравнения:
обе
части уравнения:
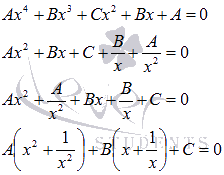 Проведем
замену переменных
Проведем
замену переменных

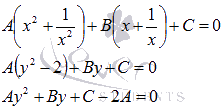 Таким
образом, возвратное уравнение четвертой
степени сводится к квадратному
уравнению.
Таким
образом, возвратное уравнение четвертой
степени сводится к квадратному
уравнению.
![]() Это
уравнение в силу симметрии коэффициентов
является возвратным. Разделим на
обе
части уравнения (х=0 корнем не
является, поэтому деление не приведет
к потере этого корня).
Это
уравнение в силу симметрии коэффициентов
является возвратным. Разделим на
обе
части уравнения (х=0 корнем не
является, поэтому деление не приведет
к потере этого корня).
![]()
 Сделаем
замену переменной
Сделаем
замену переменной
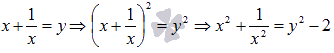
 Пришли
к квадратному уравнению. Решаем
его.
Пришли
к квадратному уравнению. Решаем
его.
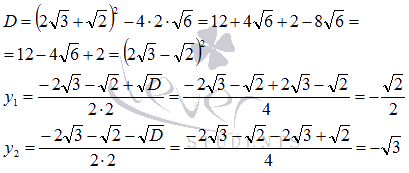 Возвращаемся
к замене:
Возвращаемся
к замене:
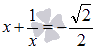 или
или
![]() .
.
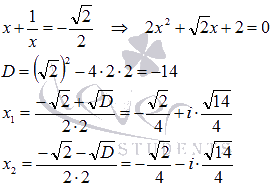
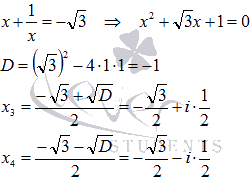 Ответ:
Ответ:
 или
или
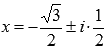 Решение
биквадратного уравнения.Уравнение
четвертой степени вида
Решение
биквадратного уравнения.Уравнение
четвертой степени вида
![]() называют
биквадратным уравнением. Заменой
называют
биквадратным уравнением. Заменой
![]() биквадратное
уравнение сводится к квадратному
биквадратное
уравнение сводится к квадратному
![]() ,
которое решается стандартным методом.Решить
биквадратное уравнение
,
которое решается стандартным методом.Решить
биквадратное уравнение
![]() Проведем
замену переменной
,
тогда исходное уравнение сведется к
квадратному:
Проведем
замену переменной
,
тогда исходное уравнение сведется к
квадратному:
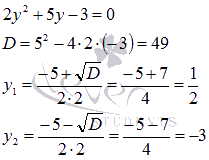 Следовательно,
Следовательно,
![]() или
или
![]() .
Из первого равенства находим
.
Из первого равенства находим
![]() ,
второе полученное уравнение действительных
корней не имеет, зато имеет пару комплексно
сопряженных корней
,
второе полученное уравнение действительных
корней не имеет, зато имеет пару комплексно
сопряженных корней
![]() Ответ:
или
Ответ:
или
Решение
уравнений четвертой степени по методу
Феррари.
В общем случае, приведенное
уравнение четвертой степени вида
![]() можно
решить методом Феррари.
Находится
можно
решить методом Феррари.
Находится
![]() -
любой из корней кубического уравнения
-
любой из корней кубического уравнения
![]()
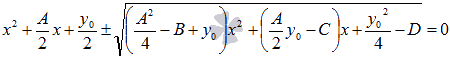 подкоренное
выражение является полным квадратом.Корни
этих уравнений являются корнями исходного
уравнения четвертой степени.Найти корни
уравнения
подкоренное
выражение является полным квадратом.Корни
этих уравнений являются корнями исходного
уравнения четвертой степени.Найти корни
уравнения
![]() Решение.
Имеем
А=3, В=3, С=-1, D=-6. Решим этот пример по
методу Феррари.
Составляем и
решаем кубическое уравнение.
Решение.
Имеем
А=3, В=3, С=-1, D=-6. Решим этот пример по
методу Феррари.
Составляем и
решаем кубическое уравнение.![]() Одним
из корней полученного кубического
уравнения является
Одним
из корней полученного кубического
уравнения является
![]() ,
так как
,
так как
![]() .
Получаем
два квадратных уравнения
.
Получаем
два квадратных уравнения
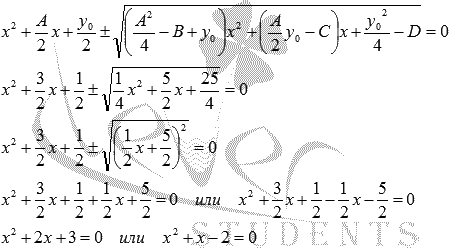 Корнями
первого уравнения являются
Корнями
первого уравнения являются
![]() ,
корнями второго х = 1 и х = -2.
Ответ:
,
корнями второго х = 1 и х = -2.
Ответ:
![]()
18)
В комбинаторике
перестано́вка — это упорядоченный
набор чисел
![]() обычно
трактуемый как биекция
на множестве
обычно
трактуемый как биекция
на множестве
![]() ,
которая числу i ставит соответствие
i-й элемент из набора. Число n при
этом называется порядком перестановки.
Как синоним слову "перестановка"
в этом смысле некоторые авторы используют
слово расстановка.
,
которая числу i ставит соответствие
i-й элемент из набора. Число n при
этом называется порядком перестановки.
Как синоним слову "перестановка"
в этом смысле некоторые авторы используют
слово расстановка.
В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову "перестановка" в этом смысле некоторые авторы используют слово подстановка. (Другие авторы подстановкой называют наглядный способ записи перестановки.)
Свойства
Число всех перестановок порядка
 равно
числу размещений
из n по n, то есть факториалу:
равно
числу размещений
из n по n, то есть факториалу:
![]()
Композиция определяет операцию произведения на перестановках одного порядка:
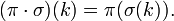 Относительно
этой операции множество перестановок
порядка n образует группу,
которую называют симметрической
и обычно обозначают
Относительно
этой операции множество перестановок
порядка n образует группу,
которую называют симметрической
и обычно обозначают
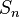 .
.Любая группа является подгруппой группы перестановок множества элементов этой группы (теорема Кэли). При этом каждый элемент
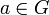 сопоставляется
с перестановкой
сопоставляется
с перестановкой
 ,
задаваемой тождеством
,
задаваемой тождеством
 где
g — произвольный элемент группы
G, а
где
g — произвольный элемент группы
G, а
 —
групповая операция.
—
групповая операция.
19) ПодстановкиПусть M -- некоторое множество. Подстановкой на M назовем взаимно однозначное отображение $a:M\rightarrow M$ множества M на себя. Обозначим через S(M) множество всех подстановок на M. Группа подстановокПусть a и b -- две подстановки из S(M). Назовем произведением ab этих подстановок композицию отображений a, b, то есть ab -- такой элемент из S(M), что m(ab)=(ma)b для всех $m\in M$Теорема. Множество S(M) является группой относительно введенной операции умножения, то есть в S(M) есть единичный элемент e со свойством: ex=xe=x для любого $x\in S(M)$; для любого $x\in S(M)$ есть $y\in S(M)$, что xy=yx=e, и операция умножения ассоциативнаДоказательство. Нам необходимо проверить три аксиомы. В S(M) имеется единичный элемент -- это тождественное отображение, которое обозначим буквой e. Известно также, что для всякого взаимно однозначного отображения x множества M на M существует обратное отображение x-1, для которого xy=yx=e. Осталось проверить аксиому ассоциативности. Пусть a, b, c -- подстановки из $S(M),\ m$ -- элемент множества M. Вычисляя образ элемента m при отображениях (ab)c и a(bc), мы убеждаемся, что эти отображения совпадают:m((ab)c)=(m(ab))c=((ma)b)c,m(a(bc))=(ma)(bc)=((ma)b)c.
20)
Войства определителей
Свойство (1) Определитель не изменится, если все строки заменить соответствующими столбцами и наоборот.
![]()
Свойство (2) При перестановке двух каких-либо строк или столбцов местами определитель изменяет знак.
![]()
Свойство (3) Определитель равен нулю, если он имеет две равные строки (столбца).
Свойство (4) Множитель, общий для всех элементов строки или столбца, можно выносить за знак определителя.
![]()
Свойство (5) Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, то определитель не изменится.
Следствие из свойств 32.4 и 32.5: Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на некоторое число, то определитель не изменится.
Свойство (6) Сумма произведений элементов какой-либо строки или столбца на алгебраические дополнения соответствующих элементов другой строки или столбца равна нулю.
21)Миноры
матрицыПусть дана квадратная
матрица
А, n - ого порядка. Минором некоторого
элемента аij , определителя
матрицы n - ого порядка называется
определитель (n - 1) - ого порядка,
полученный из исходного путем вычеркивания
строки и столбца, на пересечении которых
находится выбранный элемент аij.
Обозначается Мij. Рассмотрим на
примере определителя
матрицы 3 - его порядка:
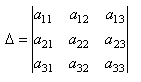
,
тогда согласно определению минора,
минором М12, соответствующим
элементу а12, будет определитель:
 При
этом, с помощью миноров можно
облегчать задачу вычисления определителя
матрицы. Надо разложить определитель
матрицы по некоторой строке и тогда
определитель будет равен сумме всех
элементов этой строки на их миноры.
Разложение определителя матрицы 3
- его порядка будет выглядеть так:
При
этом, с помощью миноров можно
облегчать задачу вычисления определителя
матрицы. Надо разложить определитель
матрицы по некоторой строке и тогда
определитель будет равен сумме всех
элементов этой строки на их миноры.
Разложение определителя матрицы 3
- его порядка будет выглядеть так:
|
|
, знак перед произведением равен (-1)n, где n = i + j.
МинорМинором
![]() элемента
элемента
![]() матрицы n-го
порядка называется определитель матрицы
(n-1)-го
порядка, полученный из матрицы А
вычеркиванием i-й
строки и j-го
столбца.
матрицы n-го
порядка называется определитель матрицы
(n-1)-го
порядка, полученный из матрицы А
вычеркиванием i-й
строки и j-го
столбца.

 При
выписывании определителя (n-1)-го
порядка, в исходном определителе элементы
находящиеся под линиями в расчет не
принимаются.Алгебраические
дополненияАлгебраическим дополнением
Аij элемента
аij матрицы
n-го порядка
называется его минор, взятый со знаком,
зависящий от номера строки и номера
столбца:
При
выписывании определителя (n-1)-го
порядка, в исходном определителе элементы
находящиеся под линиями в расчет не
принимаются.Алгебраические
дополненияАлгебраическим дополнением
Аij элемента
аij матрицы
n-го порядка
называется его минор, взятый со знаком,
зависящий от номера строки и номера
столбца:
![]()
то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.
Пример 1. Найти алгебраические дополнения всех элементов матрицы


