4.4 Понятие качества корректирующего кода
Одной из основных характеристик корректирующего кода является избыточность кода, указывающая степень удлинения кодовой комбинации для достижения определенной корректирующей способности.
Если на каждые m символов выходной последовательности кодера канала приходится k информационных и (m-k) проверочных, то относительная избыточность кода может быть выражена одним из соотношений: Rm = (m-k)/m или Rk = (m-k)/k.
Величина Rk, изменяющаяся от 0 до ¥, предпочтительнее, так как лучше отвечает смыслу понятия избыточности. Коды, обеспечивающие заданную корректирующую способность при минимально возможной избыточности, называют оптимальными.
В связи с нахождением оптимальных кодов оценим, например, возможное наибольшее число Q разрешенных комбинаций m-значного двоичного кода, обладающего способностью исправлять взаимно независимые ошибки кратности до s включительно. Это равносильно отысканию числа комбинаций, кодовое расстояние между которыми не менее d=2s+1.
Общее число различных исправляемых ошибок для каждой разрешающей комбинации составляет
,
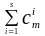где Cmi – число ошибок кратности i.
Каждая из таких ошибок должна приводить к запрещенной комбинации, относящейся к подмножеству данной разрешенной комбинации. Совместно с этой комбинацией подмножество включает комбинаций.
1+
Однозначное декодирование возможно только в том случае, когда названные подмножества не пересекаются. Так как общее число различных комбинаций m-значного двоичного кода составляет 2m, число разрешенных комбинаций не может превышать
Или
.
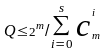Эта верхняя оценка найдена Хэммингом. Для некоторых конкретных значений кодового расстояния d, соответствующие Q укажем в таблице:
Таблица 4.3.
-
d
Q
d
Q
1
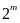
5
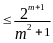
2
…
...
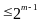
3
…
...
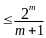
4
...
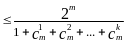
Коды, для которых в приведенном соотношении достигается равенство, называют также плотноупакованными.
Однако не всегда целесообразно стремиться к использованию кодов, близких к оптимальным. Необходимо учитывать другой, не менее важный показатель качества корректирующего кода – сложность технической реализации процессов кодирования и декодирования.
Если информация должна передаваться по медленно действующей и дорогостоящей линии связи, а кодирующее и декодирующее устройства предполагается выполнить на высоконадежных и быстродействующих элементах, то сложность этих устройств не играет существенной роли. Решающим фактором в этом случае является повышение эффективности пользования линией связи, поэтому желательно применение корректирующих кодов с минимальной избыточностью.
Если же корректирующий код должен быть применен в системе, выполненной на элементах, надежность и быстродействие которых равны или близки надежности и быстродействию элементов кодирующей и декодирующей аппаратуры. Это возможно, например, для повышения достоверности воспроизведения информации с запоминающего устройства ЭВМ. Тогда критерием качества корректирующего кода является надежность системы в целом, то есть с учетом возможных искажений и отказов в устройствах кодирования и декодирования. В этом случае часто более целесообразны коды с большей избыточностью, но простые в технической реализации.