2. Законы отражения и преломления света; пол­ное внутреннее отражение; линзы; формула тонкой линзы; оптические приборы.

Если световой пучок падает на поверхность, разделяющую две прозрачные среды разной оптической плотности, например воздух и воду, то часть света отражается от этой поверхности, а другая часть — проникает во вторую среду. При переходе из одной среды в другую луч света изменяет направление на границе этих сред. Это явление закреплено в законе отражения и преломле­нием света: « Луч падающий, отраженный и перпендикуляр, восстановленный в точке падения луча лежат в одной плоскости. Угол падения равен углу отражения», и « Луч падающий, преломленный и перпендикуляр, восстановленный в точке падания луча, лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред и называется показателем преломления второй среды относительно первой». , где  - относительный показатель преломления (показатель преломления второй среды относительно первой),  -угол падения,  -угол преломления,  -скорость распространения света в первой среде,  - скорость распространения света во второй среде.

При некотором значении угла падения, угол преломления станет равным 90⁰, т.е. наступит полное отражение света.

Линзой называют прозрачное тело, ограниченное сферическими поверхностями. Линзы бывают выпуклые и вогнутые. Выпуклая линза является собирающей, а вогнутая – рассеивающей. Любая линза имеет фокус – точку, в которой собираются все лучи, прошедшие через линзу и оптическую силу – величину обратную фокусному расстоянию. Если перед линзой расположить некоторый предмет, то можно построить его изображение, используя формулу тонкой линзы.

1 / d + 1 / f = 1 /F,где d – расстояние от предмета до линзы, f – расстояние от линзы до изображения, F – фокусное расстояние.

3. Задача по теме «Вес движущегося тела».

Билет № 18

1. Связь между давлением идеального газа и сред­ней кинетической энергией теплового движения его молекул. Уравнение состояния идеального газа. Изопроцессы   Состояние данной массы газа полностью определено, если известны его давление, температура и объем. Эти величины называют параметрами состояния газа. Уравнение, связывающее параметры состояния, называют уравнением состояния.     Для произвольной массы газа состояние газа описывается уравнением Менделеева—Клапейрона: pV = mRT/M, где р — давление, V — объем, m — масса, М — молярная масса, R — универсальная газовая постоянная. Физический смысл универсальной газовой постоянной в том, что она показывает, какую работу совершает один моль идеального газа при изобарном расширении при нагревании на 1 К (R = 8,31 ДжДмоль • К)).           Уравнение Менделеева—Клапейрона показывает, что возможно одновременное изменение трех параметров, характеризующих состояние идеального газа. Однако многие процессы в газах, происходящие в природе и осуществляемые в технике, можно рассматривать приближенно как процессы, в которых изменяются лишь два параметра. Особую роль в физике и технике играют три процесса: изотермический, изохорный и изобарный.           Изопроцессом называют процесс, происходящий с данной массой газа при одном постоянном параметре — температуре, давлении или объеме. Из уравнения состояния как частные случаи получаются законы для изопроцессов.           Изотермическим называют процесс, протекающий при постоянной температуре. Т = const. Он описывается законом Бойля—Мариотта: pV = const.           Изохорным называют процесс, протекающий при постоянном объеме. Для него справедлив закон Шарля: V = const, p/T = const.           Изобарным называют процесс, протекающий при постоянном давлении. Уравнение этого процесса имеет вид V/T = const прир = const и называется законом Гей-Люссака. Все процессы 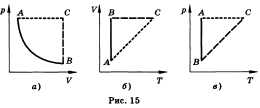м ожно изобразить графически (рис. 15).           Реальные газы удовлетворяют уравнению состояния идеального газа при не слишком высоких давлениях (пока собственный объем молекул пренебрежительно мал по сравнению с объемом сосуда,  в котором находится газ) и при не слишком низких температурах (пока потенциальной энергией межмолекулярного взаимодействия можно пренебречь по сравнению с кинетической энергией теплового движения молекул), т. е. для реального газа это уравнение и его следствия являются хорошим приближением.