9. Фиктивные переменные в множественной регрессии

Фиктивными принять называть качественные факторы, имеющие конечное число градаций. Например, пол, социальное положение, климатическая зона и т.п. Пусть урожайность яровой пшеницы y зависит от вида вспашки (зяблевая, весенняя) и количества удобрений х (т/га), внесенных во время сева. Влияние удобрений предварительно исследовалось по 25 опытным участкам, из которых 13 было с зяблевой вспашкой, а 12 с – с весенней, и привело к построению модели в виде

Y = b₀ + b₁x = 11,46 + 0,326x,

при этом коэффициент детерминации получился равным 0,525.

Добавим фиктивную переменную

и построим новое уравнение теперь уже множественной регрессии

Y = b₀ + b₁x + b₂z

Обычная процедура нахождения коэффициентов приводит к следующим результатам b₀ = 9,91; b₁ = 0,33; b₂ = 2,91, при этом коэффициент детерминации увеличивается до значения 0,766. Из этого следует, что применение зяблевой вспашки увеличивает урожай на 2,9 ц/га, а учет вида вспашки делает модель более точной.

Число градаций фиктивной переменной может быть больше 2. В этом случае увеличивают общее число фиктивных переменных таким образом, чтобы их число стало на 1 меньше числа градаций. Например, изучается зависимость цены 2-х комнатной квартиры в зависимости от ее площади и типа дома – кирпичный, панельный “хрущевка”. Поскольку градаций три, вводим 2 фиктивных переменных.

Предположим, что уравнение регрессии с такими фиктивными переменными получилось в виде

Y = 320 + 500x + 2200z + 1600v

Наиболее дорогими, согласно этому уравнению, являются квартиры в панельных домах, а самыми дешевыми – в “хрущевках”.

В сложных случаях в уравнение регрессии приходится включать несколько фиктивных переменных, каждая из которых имеет более 2-х градаций. Например, потребление есть в основном функция дохода, однако для более точного исследования может понадобиться включение таких факторов, как пол, социальная группа, национальность, возрастная категория и т.д. Возможно построение уравнения регрессии на исключительно фиктивных переменных. Например, зависимость уровня заработной платы в зависимости от региона. В любом случае число фиктивных переменных также должно быть на 1 меньше общего числа градаций.

10. Системы эконометрических уравнений

В реальных задачах экономики факторы х₁, х₂…х_m, оказывающие влияние на результирующий признак у, часто взаимосвязаны между собой, что нарушает предпосылки МНК и делает непригодными ранее рассмотренные методы оценки параметров регрессионных моделей. Кроме того, обычной является ситуация, когда некая экономическая величина, будучи зависимой от некоторой другой, сама является фактором для некоторой третьей. Так расходы общества на потребление зависят от валового национального дохода (ВНД), но ВНД зависит от объема инвестиций, инвестиции же, кроме прочего, зависят от темпов роста ВНД и т.д.

Все это порождает понятие системы эконометрических уравнений в виде структурной формы модели (СФМ), которая в самом общем виде имеет вид

(10.1)

Существенным для дальнейшего является то, что ни одно из уравнений СФМ (9.1) не может рассматриваться самостоятельно, и для нахождения их параметров неприменимы ранее рассмотренные методы. Примером СФМ может служить известная модель динамики цен Y₁ и заработной платы Y₂

где х₁ – процент безработицы,

х₂ – темп изменения постоянного капитала,

х₃ – темп изменения цен на импорт сырья.

Переменные Y_k, k = 1,2...n называют эндогенными (зависимыми)_, х_i, i = 1,2...m – экзогенными (независимыми, предопределенными). Экономические переменные в одних моделях могут выступать как эндогенные, а в других, - как экзогенные. В качестве последних могут рассматриваться эндогенные за прошедшие периоды времени (лаговые переменные). Как правило, экзогенные переменные являются объектом регулирования с целью достижения желаемых значений эндогенных. По возможности, переменные в СФМ стараются представить в виде отклонений от средних. Это позволяет избавиться от т.н. свободных членов уравнений и несколько упростить процедуру нахождения ее параметров.

Если экзогенные переменные можно считать взаимно независимыми, то можно преобразовть СФМ в т.н. приведенную форму (ПФМ) вида

(9.2)

В правой части ПФМ находятся только независимые переменные и для нахождения ее параметров δ_kj вполне подходит МНК. Коэффициенты ПФМ являются нелинейными алгебраическими функциями от коэффициентов СФМ. Например, дана СФМ вида

(10.3)

и соответствующая ей ПФМ

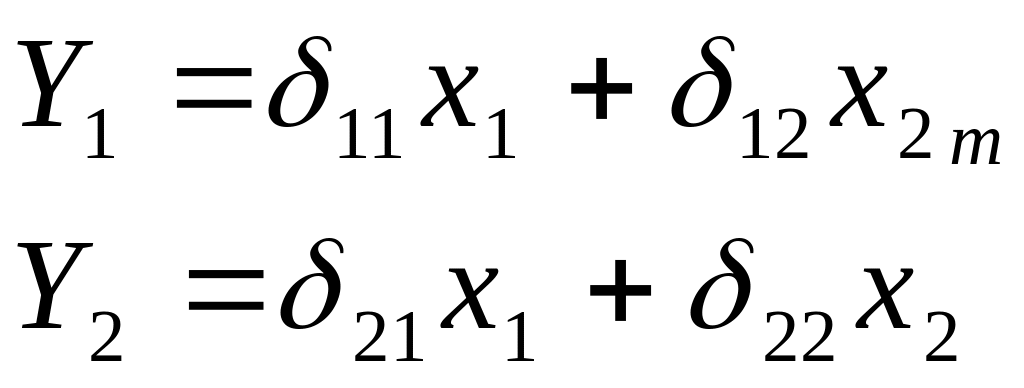(10.4)

Выразив из первого уравнения (10.3) Y₂ и подставив это выражение во второе уравнений (10.3), получим после элементарных преобразований

,

т.е. первое уравнение ПФМ, в котором

По аналогичной схеме можно получить и второе уравнение (10.4) в виде

,

в котором

.

Согласно модели Кейнса потребление Y₁, доход Y₂ и инвестиции в основной капитал х связаны СФМ вида

Второе уравнение в этой модели по причине отсутствия неизвестных коэффициентов в эконометрике называется тождеством. Соответствующая ПФМ

Каждое из этих уравнений представляет собой линейную парную регрессию, параметры которой без особого труда могут быть найдены с помощью МНК по эмпирическим данным. Далее, подставляя в первое уравнение ПФМ выражение для х из второго, получаем исходную СФМ. В данном случае однозначный переход от ПФМ к исходной СФМ возможен, но это не всегда так. Определение возможности такого перехода составляет т.н. проблему идентификации.

Эта проблема состоит в однозначности перехода от ПФМ к СФМ, а ее возникновение связано с различным числом неизвестных параметров в исходной СФМ и соответствующей ей ПФМ. Сравним, например, СФМ

(10.5)

и соответствующую ей ПФМ

(10.6)

В системе (9.5) 8 неизвестных коэффициентов, что соответствует формуле n(n-1+m), где n –число эндогенных, а m – число экзогенных переменных. В (9.6) 6 неизвестных коэффициентов, что вытекает из общей формулы n^.m. При переходе от ПФМ к СФМ необходимо из 6 соотношений найти 8 неизвестных, что невозможно, если не сделать каких-то дополнительных предположений, компенсирующих два недостающих уравнения. Примером таковых дополнительных соотношений для системы (9.5) могут быть a₁₂ = a₂₃ = 0, сделанные на основе анализа конкретной задачи или что-либо подобное.

Модель называется идентифицируемой, если число параметров СФМ и ПФМ одинаково, либо имеются дополнительные условия, позволяющие однозначно определить параметры СФМ через параметры ПФМ.

Модель неидентифицируема, если число параметров СФМ больше числа параметров ПФМ и нет компенсирующих это дополнительных условий.

Модель сверхидентифицируема, если число параметров ПФМ больше числа параметров СФМ.

Известны необходимые условия отнесения СФМ к одному из этих классов, называемые счетным правилом.

1. СФМ идентифицируема, если идентифицируемо каждое уравнение системы.

2. СФМ неидентифицируема, если неидентифицируемо хотя бы одно уравнение системы.

3. СФМ сверхидентифицируема, если сверхидентифицируемо хотя бы одно ее уравнение и нет неидентифицируемых.

Обозначив через Н число эндогенных переменных системы, а через D – число экзогенных, имеющихся в системе, но не входящих в данное, условия отнесения к одному из трех перечисленных типов формулируются следующим образом:

1. D +1 = H; 2. D + 1 < H; 3. D + 1 > H.

Например, дана СФМ вида

(10.7)

В первом уравнении этой системы три эндогенных переменных и не хватает 2-х экзогенных (х₃, х₄). В результате имеем D + 1 = H, т.е. уравнение идентифицируемо. То же самое справедливо и для двух оставшихся уравнений. Таким образом СФМ (9.7) идентифицируема Это означает, что возврат от соответствующей ей ПФМ к СФМ возможен и единственен без каких-либо дополнительных условий.

Предположим теперь, что в системе (10.7) a₂₁ = a₂₃ =0. Первое и третье уравнения не изменились и, следовательно, остались идентифицируемыми. Для второго уравнения D = H = 2 и оно становится, как и вся система, сверхидентифицируемым. Наконец, если бы третье уравнение имело вид

,

то оно считалось бы неидентифицируемым, что и всю систему делает неидентифицируемой.

Если в СФМ входят тождества (см. выше модель Кейнса), проверять их на идентифицируемость не надо, т.е. суждение о идентифицируемости системы осуществляется только по входящим в ее состав уравнениям.