15. Экспоненциальное сглаживание

Общим недостатком рассмотренных выше SMA и WMA методов сглаживания является то, что результат относится к середине интервала сглаживания. Для целей прогноза наибольшую ценность представляет последний уровень ряда, отражающий текущие значения внешних факторов, влияющих на данный показатель. Прошлые значения ВР в этом смысле менее информативны и должны учитываться с понижающими коэффициентами. Эти положения реализованы в методе экспоненциального сглаживания (Exponential Moving Average – EMA) и его модификациях.

Согласно методу ЕМА нулевого порядка сглаженное значение ВР в момент времени t

, (15.1)

где 0 < α < 1 – параметр метода.

Формулы типа (15.1) называются в математике рекуррентными, т.е. позволяющими по предыдущему значению найти последующее. Действительно, если известен ВР y_t, t = 1,2,..., то, задавшись тем или иным образом Y₁, например, Y₁ = y₁ и параметрами α, β, нетрудно вычислить

(15.2)

Легко заметить, что:

1. Y_t является взвешенной суммой всех предыдущих значений y_t,

2. результат усреднения относится к моменту времени t,

3. чем дальше от конца интервала усреднения находится уровень ряда, тем меньше его вклад в формирование усредненного значения, причем степень уменьшения этого влияния определяется параметром α.

Доказано, что математическое ожидание E[Y_t] = E[y_t], если y_t = const + ε_t, где ε_t – случайные, некоррелированные между собой остатки, имеющие нормальный закон распределения. Дисперсия сглаженного ВР

,

т.е. чем меньше α, тем сильнее степень сглаживания.

В качестве прогноза ВР для момента t+1 в методе ЕМА нулевого порядка выбирается значение Y_t . Поскольку выражение (15.1) можно представить в виде

Y_t = Y_t-1 + α(y_t – Y_t-1),

получается, что прогнозируемое значение представляет собой коррекцию предыдущего прогноза, т.е. к предыдущему прогнозу Y_t-1 прибавляется ошибка прогноза с коэффициентом α. Это обстоятельство позволяет отнести ЕМА к т.н. адаптивным методам сглаживания, в которых коррекция предыдущего прогноза является ключевым понятием.

Если наряду с уровнями ВР ввести в рассмотрение его приращения (первые разности)

Δy_t = y_t – y_t-1, t = 2,3,...n

и применить к полученному таким образом новому ВР ту же процедуру ЕМА, то прогноз

соответствует методу ЕМА 1-го порядка. Считается, что такой прогноз при определенных обстоятельствах более точен. Введение в рассмотрение ВР вторых разностей (разностей от первых разностей) порождает метод ЕМА 2-го порядка и т.д.

Важным свойством ЕМА, как, впрочем, и всех рекурсивных методов, является то, что при расчете очередного сглаженного значения Y_t не надо обращаться ко всем предыдущим уровням ряда y_t-1, y_t-2,...y₁, а достаточно знать лишь значение Y_t-1, в котором сконцентрирована вся информация об этих величинах.

16. Выявление структурных изменений временного ряда

К роме циклических колебаний возможно единовременное изменение параметров тенденции, обусловленное изменением параметров внешней среды (начало реформ, экономические и политические кризисы, смена режима и т.п.). Примерный вид уровней такого ВР показан точками на рисунке 16.1.

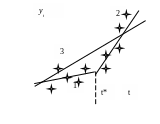
Рис. 16.1. Временной ряд с предполагаемыми структурными изменениями

В таких случаях интересно выявить момент времени t^*, а затем и событие, повлиявшее на ВР y(t). Иногда, наоборот, хотят оценить степень влияния того или иного уже произошедшего в момент времени t^* события на уровни ВР. Здесь возможны два подхода. При первом мы признаем влияние события, произошедшего в момент времени t^*, и строим два уравнения регрессии – до и после этого момента (линии 1, 2 на рисунке 16.1). При втором – пренебрегаем влиянием изменений внешней среды и строим единое уравнение регрессии на весь диапазон аргумента. В первом варианте мы уменьшаем ОСК на каждом из участков, но проигрываем в точности из-за малого числа наблюдений, участвующих в построении регрессии. Во втором, наоборот, - ОСК увеличивается, а точность оценок параметров регрессии уменьшается. Имеется формальная процедура выбора одного из этих подходов, получившая название тест Чоу (Chow).

Введем систему обозначений, представленных в таблице 16.1

№	Вид уравнения регрессии	Число на- блюдений	ОСК	Число па- раметров	Число степе- ней свободы	Модель
1	y1(t)=a1+b1t	n1	C1	k1	n1-k1	Кусочно- линейная
2	y2(t)=a2+b2t	n2	C2	k2	n2-k2
3	y3(t)=a3+b3t	n = n1+n2	C3	k3	n-k3=n1+n2-k3	Единая

Как всегда при проверке статистических гипотез выдвигается нулевая гипотеза Н₀ о структурной стабильности и альтернативная Н₁ о наличии структурных изменений. Обозначим С_кл = С₁ + С₂ как ОСК для кусочно – линейной модели с числом степеней свободы (n₁- k₁) + (n₂ - k₂) = n - k₁- k₂. Величиной ΔС = С₃ – С_кл будем оценивать степень повышения точности кусочно - линейной модели по сравнению с единой. Число степеней свободы для нее n – k - (n - k₁ - k₂) = k₁ - k₂ –k₃ . Чоу показал, что отношение

имеет стандартное F-распределение с (k₁ - k₂ –k₃) и (n - k₁- k₂) степенями свободы.

Таким образом, задавшись уровнем значимости α и вычислив по эмпирическим данным величину F, мы при

отклоняем гипотезу Н₀ и принимаем Н₁, т.е. считаем целесообразной кусочно – линейную модель. В противном случае считаем более подходящей единую модель. В частном случае при k₁=k₂=k₃=k