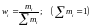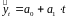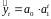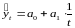Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий.
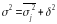 (6.16)
(6.16)
Зная любые два вида дисперсий, всегда можно найти или проверить правильность расчета третьего вида.
 (6.16а)
(6.16а)
 (6.16б)
(6.16б)
Правило сложения дисперсий позволяет оценить степень влияния группировочного признака на результативный признак и количественно измерить степень этого влияния.
Для этого применяется коэффициент детерминации, который показывает степень колеблемости в процентах результативного признака в зависимости от степени колеблемости факторного и рассчитывается как отношение факторной дисперсии к общей дисперсии результативного признака.
Ряды динамики 21-26
Ряд расположенных во времени статистических данных, изменение которых отражает закономерность развития изучаемого явления, называется рядом динамики или временным рядом.

Средний уровень ряда динамики определяется в соответствии со следующими формулами:
|
Интервальный ряд |
Моментный ряд |
Средний уровень ряда |
средняя арифметическая |
средняя хронологическая |
Показатель |
Цепной |
Базисный |
Абсолютный прирост |
|
|
Коэффициент роста |
|
|
Темп роста |
|
|
Коэффициент прироста |
|
|
Темп прироста |
|
|
Абсолютное значение (содержание) одного процента прироста |
|
|
Пункты роста |
|
|
Средний коэффициент роста |
или
|
|
Средний коэффициент прироста |
|
|
Средний темп роста |
|
|
Для приведения
рядов к одному основанию выбирается
один, общий для всех рядов начальный
период, который берется за 100%.
Смыкание рядов возможно, если ряды имеют хотя бы один общий период Одной из важнейших задач статистики является выявление в рядах динамики основной тенденции развития явления


Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики
Метод скользящей средней основан на том, что исчисляется средний уровень из определенного числа первых уровней ряда, а затем из того же числа уровней ряда, но уже начиная со второго по счету и т.д.
Метод аналитического
выравнивания основывается на
том, что общая тенденция рассчитывается
как функция времени:
 .
Определение теоретических уровней
.
Определение теоретических уровней
 производится на основе адекватной
математической модели, в качестве
которой могут выступать линейная,
показательная, экспоненциальная и
другие функции, представленные в таблице
8.16.
производится на основе адекватной
математической модели, в качестве
которой могут выступать линейная,
показательная, экспоненциальная и
другие функции, представленные в таблице
8.16.
Вид уравнения |
Отражаемая уравнением тенденция развития |
Уравнение прямой
|
Равномерный рост при а1>0 или равномерное падение при а1<0 |
Показательная функция
|
Ускоряющийся рост при а1>0 или ускоряющееся падение при а1<0 |
Гипербола
|
Замедляющееся падение при а1>0 или замедляющийся рост при а1<0 |
Парабола
|
Рост, переходящий в падение, или
падение, переходящее в рост в точке
|




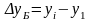



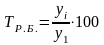





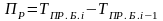

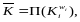 где Ki
– цепной коэффициент роста в i-ом
периоде; wi
– вес i-ого
периода, исчисляемый как
где Ki
– цепной коэффициент роста в i-ом
периоде; wi
– вес i-ого
периода, исчисляемый как