3.1.7.3 Определение оптимальной траектории посадки одиночного воздушного судна

Оптимальная траектория одиночного ВС tr, доставляющая минимум рассмотренному критерию (3.1), определяется минимальной своей длинной между точками ТВХ и ТНС. Этой длине будет соответствовать минимальный интервал времени Т_гм в выражении (3.5), так как значение координат всех остальных характерных точек (ТГП, ТВГ, ТК) и параметров траекторий посадки известны и практически постоянны (и не могут быть изменены) для одинаковых типов ВС.

Таким образом, рассматриваемая задача состоит в определении кратчайшей траектории полета ( кратчайшего пути) для i-го ВС между точками ТВХ_i и ТНС из множества допустимых для i-го ВС траекторий (TR_i) для выполнения посадки i-го ВС, появившегося в момент времени t в точке (Х, Y) входа в аэродромное ВП на высоте h. Рассматриваемая задача решается с помощью следующих построений.

Для определения множества TR-допустимых траекторий посадки одиночного ВС из двух центров разворотов в точке ТВХ (Ц_RТBX и Ц_LТBX) проведем векторы Q;\s \up0(¯_ij в два центра разворотов в точке ТНС (Ц_RТНС и Ц_LТНС). Таких векторов будет четыре:

— векторы Q;\s \up0(¯₁₁ и Q;\s \up0(¯₁₂ имеют началом точку Ц_RТBX и оканчиваются в точках Ц_RТНС и Ц_LТНС соответственно;

— векторы Q;\s \up0(¯₂₁ и Q;\s \up0(¯₂₂ начинаются в точке Ц_LТBX и оканчиваются в точках Ц_RТНС и Ц_LТНС соответственно.

Координаты точек начала и конца этих векторов обозначим (Х, Y) и (Х, Y), тогда модули этих векторов будут определяться выражениями

Q_ij  |Q;\s \up0(¯_ij|   , где Х\S \up1(= Х  X; Y\S \up1(= Y  Y,

а направление — азимутом A_ij (углом между северным направлением меридиана, проходящего через центр разворота, и линией, соединяющей центры окружностей, точек ТВХ и ТНС, отсчитываемый по ходу часовой стрелки) в пределах от 0 до 360.

Азимуты векторов Q;\s \up0(¯_ij вычисляются с помощью рассмотренной функции А по модулю В:

A_ij  (arctg  2) mod 2.

При определении значения углов в градусах используется известное соотношение _[град]  _[рад]180/.

Для выполнения посадки любого ВС, в общем случае из всего множества допустимых для него траекторий предпочтительными являются, как правило, не более четырех траекторий TR={tr_j; j  1, 2, 3, 4}, среди которых существуют и оптимальные (самые короткие), доставляющие минимум критерию (3.1). Конкретное число таких траекторий зависит от расстояний между центрами разворотов в точках ТВХ и ТНС.

Если существует такой вектор Q;\s \up0(¯_ij, модуль которого Q_ij< 2r , то траектории виражей радиуса r в точках ТВХ и ТНС пересекаются (рисунок 3.27). В этом случае существует не более трех траекторий движения между точками ТВХ и ТНС TR  {tr_1, tr_2, tr₃}, среди которых имеется хотя бы одна кратчайшая.

Первая возможная траектория посадки ВС (tr₁) включает следующие элементы:

— разворот вправо по окружности с центром в точке Ц_RТВХ на угол ;

— касательную прямую к окружностям с центрами Ц_RТВХ и Ц_RТНС;

— разворот вправо по окружности с центром в точке Ц_RТНС на угол .

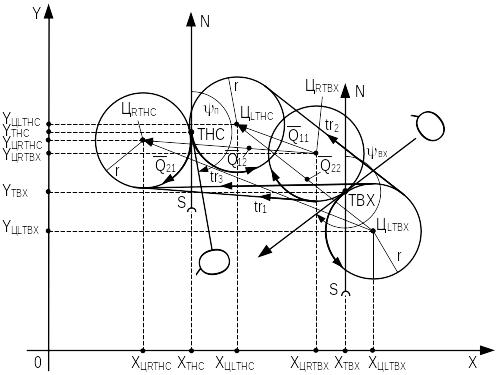
Рисунок 3.27 — Траектории виражей точек входа и посадки пересекаются

Угол разворота вправо  по окружности с центром Ц_RТBX до азимута касательной определяется как разность азимута А₁₁ вектора Q;\s \up0(¯₁₁ и курса ВС _вх:

\s \up1(1  ((А₁₁  _вх)  2) mod 2.

Интервалы времени, необходимые для первого разворота с центром в точке Ц_RТBX и движения по прямой параллельной векторуQ;\s \up0(¯₁₁ до точки начала второго правого разворота определяются выражениями:

Т\S \up1(1  , Т₁₁  .

Угол второго разворота вправо  по окружности с центром Ц_RТНС от точки конца касательной до точки ТНС определяется выражением:

  ((_п  А₁₁)  2) mod 2,

а интервал времени, необходимый для этого Т\S \up1(2  /.

Тогда, полное время полета ВС по траектории tr₁ между точками ТВХ и ТНС будет определяться выражением:

T\S \up1(п    (\s \up1(1  ).

Вторая возможная траектория посадки ВС (tr₂) включает:

— разворот влево по окружности с центром в точке Ц_LТВХ на угол ;

— касательную прямую к окружностям с центрами Ц_LТВХ и Ц_LТНС;

— разворот влево по окружности с центром в точке Ц_LТНС на угол .

Параметры движения ВС по указанным элементам траектории tr₂ определяются следующими соотношениями:

  ((_вх  А₂₂)  2) mod 2;

Т\S \up1(1   ; Т₂₂   ;

\S \up1(2  ((А₂₂  _п)  2) mod 2;

Т\S \up1(2   .

Тогда полное время полета ВС по траектории tr₂ между точками ТВХ и ТНС будет определяться выражением:

T\S \up1(п    (\s \up1(2  ).

Третья возможная траектория посадки ВС (tr₃) включает:

— разворот влево по окружности с центром в точке Ц_LТВХ на угол \s \up1(3;

— касательную прямую к окружностям с центрами Ц_LТВХ и Ц_RТНС;

— разворот вправо по окружности с центром в точке Ц_RТНС на угол \S \up1(3.

Эта траектория будет длиннее первых двух за счет более длинных виражей по окружностям с центрами ЦLТВХ и ЦRТНС даже при возможном равенстве длин прямолинейных участков траекторий.

Таким образом, определение оптимальной траектории посадки ВС будет связано со следующими решающими правилами:

— если (Т\S \up1(п  Т\S \up1(п)  0, то оптимальной является траектория tr₁ и T^по=Т\S \up1(п;

— если (Т\S \up1(п  Т\S \up1(п)  0, то оптимальной является траектория tr₂ и T^по=Т\S \up1(п;

— если (Т\S \up1(п  Т\S \up1(п)  0, то обе траектории оптимальны и можно использовать любую из них.

В том случае, когда для любого из векторов Q;\s \up0(¯_ij справедливо соотношение |Q;\s \up0(¯_ij|  2r (см. рисунок 3.28), число возможных допустимых и наиболее коротких траекторий полета ВС между точками ТВХ и ТНС будет равно четырем (TR  {tr_1, tr_2, tr₃, tr₄}). Параметры этих траекторий и периоды времени, необходимые для совершения посадки находятся с помощью построений, аналогичным рассмотренным выше. В этом случае оптимальной будет являться некоторая j-ая траектория посадки, которой соответствует минимальное время Т\s \up1(п, при j=1, 2, 3, 4:

Т\S \up1(оп  min{Т\S \up1(п_, Т\S \up1(п_, Т\S \up1(п, Т\S \up1(п}.

Рисунок 3.28 — Траектории виражей точек входа и посадки не пересекаются