3.1.7.2 Определение параметров траектории посадки воздушных судов

Интервал времени T^п, требуемый для выполнения посадки одиночного ВС и определяемый от момента оценки параметров его траектории в точке с координатами Х₀, Y₀, h₀ до момента касания ВПП, определяется суммой следующих интервалов времени:

Т^п  Т_об  Т_гм  Т_сн  Т_гп  Т_гл , (3.5)

где Т_об — время (константа аэродрома) от момента входа ВС в ВП аэродрома в точке Х₀, Y₀, h₀ до точки входа на траекторию посадки (ТВХ), требуемое для обработки радиолокационных и полетных данных о ВС, оценки параметров его движения, принятия решения о посадке и передачи на борт команды начала маневра посадки в точке ТВХ (в это время ВС сохраняет начальную скорость V₀, крен γ₀ и высоту полета h₀  h_вх); Т_гм — минимизируемое время горизонтального маневрирования ВС по схеме «разворот-прямая-разворот» от точки ТВХ до точки ТНС на высоте h_вх; Т_сн — время снижения ВС с высоты h_вх до высоты h_ТВГ между точками ТНС и ТГП под углом снижения _сн, максимально допустимом для данного типа ВС (Т_сн  (h_вх  h_ТВГ)/V_cн; V_cн  V₀ sin _сн — скорость снижения ВС); Т_гп — время (константа аэродрома) прямолинейного горизонтального полета на высоте h_ТВГ между точками ТГП и ТВГ (за это время скорость ВС должна быть снижена до скорости посадки V_п и установлен посадочный курс _п); Т_гл — время полета по глиссаде посадки со скоростью V_п от точки ТВГ до точки касания ВПП (Т_гл  S_гл/V_п; S_гл   — длина глиссады; L_ТВГ — константа аэродрома, определяющая удаление ТВГ по горизонтали от точки касания ВПП).

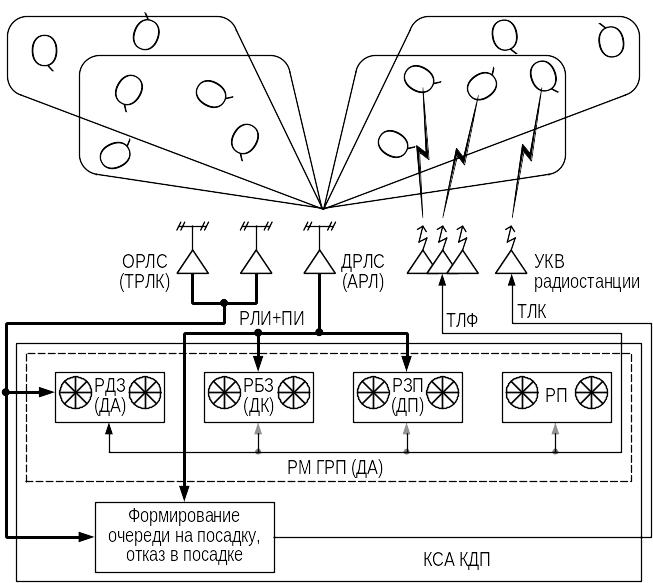
Рисунок 3.24 — Структура автоматизированного КДП

ОРЛС — обзорная РЛС; ТРЛК — трассовый радиолокационный комплекс; ДРЛС — диспетчерская РЛС; АРЛ — аэродромный радиолокатор; РЛИ — радиолокационная информация; ПИ — полетная информация; РП — руководитель полетов; РМ ГРП — рабочие места группы руководства полетами; ДА —диспетчеры аэродрома; ТЛФ —телефонный канал связи; ТЛК —телекодовый канал связи; РЗП —руководитель зоны посадки (ДП —диспетчер посадки); РДЗ —руководитель дальней зоны (ДП —диспетчер подхода); РБЗ —руководитель ближней зоны (ДК —диспетчер круга)

Координаты точки ТНС определяются следующим образом (см. рисунок 3.23)

X_ТНС  X_ТК  (L_ТВГ  L_ГП  L_СН) sin_п; Y_ТНС  Y_ТК  (L_ТВГ  L_ГП  L_СН) cos_п,

где X_ТК, Y_ТК — координаты точки касания (ТК) воздушным судном ВПП; L_ГП  V_срТ_гп — расстояние по горизонтали между точками ТВГ и ТГП; V_ср  (V₀  V_п)/2 — средняя скорость горизонтального прямолинейного полета между точками ТВГ и ТГП; L_СН  (h_вх  h_ТГП)сtg_сн — расстояние по горизонтали между точками ТГП и ТНC.

Координаты точек входа в ВП аэродрома Х_вх, Y_вх ВС с учетом времени на обработку Т_об определяются для двух вариантов начальных условий:

— ВС входит в ВП аэродрома без крена (₀=0), по прямой на ДПРМ, имея координаты Х₀, Y₀, h₀ и курс ₀, тогда

Х  V₀Т_об sin₀, Y  V₀Т_об cos₀ и Х_вх  Х₀  Х, Y_вх  Y₀  Y. (3.6)

— ВС входит в ВП аэродрома с креном (₀  0) в направление на ДПРМ, имея координаты Х₀ ,Y₀, h₀ и курс ₀. Другими словами, ВС в данной точке находится в состоянии выполнения разворота (при 0 — вправо, при <0 —влево). На интервале времени Т_об этот разворот должен быть завершен в точке ТВХ с курсом _вх. Текущий курс ВС  изменяется от значения ₀ до значения _вх на величину  (реализуется управление по изменению курса ВС), которая при правом развороте имеет положительное значение, а при левом —отрицательное и определяется соотношением

   tg₀ T_об.

Если в процессе выполнения разворота с креном ₀ на интервале времени Т_об воздушное судно пересекает северное направление меридиана, то в момент пересечения текущее значение курса   ₀   при правом развороте обнуляется, а при левом развороте принимает значение 360. Разворот выполняется до момента выхода ВС в точку ТВХ с курсом   _вх.

При вычислении значений курсового угла   ₀  , которые по физическому смыслу всегда являются положительными и меньше 360, возможно получение как отрицательных, так и положительных значений 360 (за счет положительных или отрицательных значений ). Для предотвращения такого рода ошибок применяется специальный способ функционального преобразования одной величины в другую (вычисление значения «А по модулю В» — А mod B). Смысл этого способа поясняет следующее выражение: А mod B  С, где С  А  nВ; n  0, 1, 2, ..., m. Другими словами, А mod B есть либо сама величина А (при А0 и А<В, т.к. n  0), либо значение остатка от операции вычитания из величины А целого числа (кратного количества) величины В (при А0 и АВ, т.к. n0).

При вычислении значений курсовых углов или углов каких-либо направлений движения (азимутов) в качестве величины В используются значения 360 (или 2), а в качестве величины А — суммы (₀360) или (₀2) соответственно. Слагаемые 360 (или 2) позволяют перейти от возможных отрицательных значений суммы (₀) к положительным (₀360), не изменяя существо процедуры вычисления истинного значения курсового угла, которые всегда будут удовлетворять условию 0≤<360).

Таким образом, значение курса ВС в точке ТВХ _вх при управлении  в точке (Х₀,Y₀) будет определяться выражениями:

_вх  (₀360) mod 360, если углы исчисляются в градусах, или

_вх  (₀++2) mod 2, если углы исчисляются в радианах.

Для пояснения рассмотрим два примера:

1. Пусть ₀  20, а   40 (см. рисунок 3.25 а), тогда

_вх  ((2040)+360) mod 360  340 mod 360  340.

2. Пусть ₀  350, а   40 (см. рисунок 3.25 б), тогда

_вх  ((350+40)+360) mod 360  750 mod 360  7502360 =30.

В рассматриваемом варианте начальных условий поправки Х и Y для расчета координат Х_вх, Y_вх по рассмотренным выше выражениям (см. формулу 3.6) определяются следующими соотношениями:

Х   (cos₀  cos_вх); Y   (sin_вх  sin₀),

где g — ускорение свободного падения.

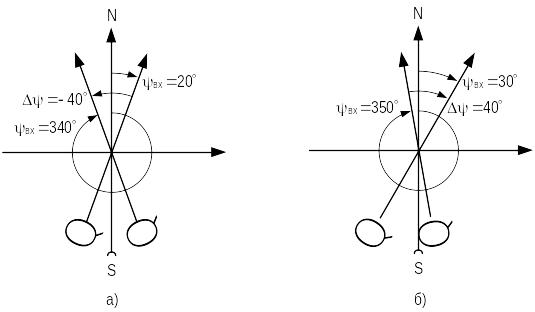
Рисунок 3.25 — Примеры вычисления значений курсовых углов и азимутов направлений

В точке ТВХ с координатами Х_вх, Y_вх, h_вх и курсом _вх ВС начинает выполнение разворота в горизонтальной плоскости на высоте h_вх с радиусом r и угловой скоростью  (см. рисунок 3.23), определяемым по формулам:

r   ;    ,

где значение r может быть отрицательным, так как tg()  tg.

Тогда координаты центров окружностей при правом (Ц_RТВХ) и при левом (Ц_LТВХ) разворотах в точке ТВХ с учетом знака r определяются следующими соотношениями (см. рисунок 3.26):

X  X_ТВХ  r cos_вх, Y  Y_ТВХ  r sin_вх;

X  X_ТВХ  r cos_вх, Y  Y_ТВХ  r sin_вх.

Вход в точку начала снижения с координатами Х_ТНС, Y_ТНС, h_вх осуществляется путем разворота ВС вправо R или влево L с радиусом r и угловой скоростью  (см. рисунок 3.23). Координаты центров разворотов Ц_RТНС, Ц_LТНС в точке ТНС с учетом знака r определяются следующими соотношениями:

X  X_ТВХ  r cos_п, Y  Y_ТВХ  r sin_п;

X  X_ТВХ  r cos_п, Y  Y_ТВХ  r sin_п.

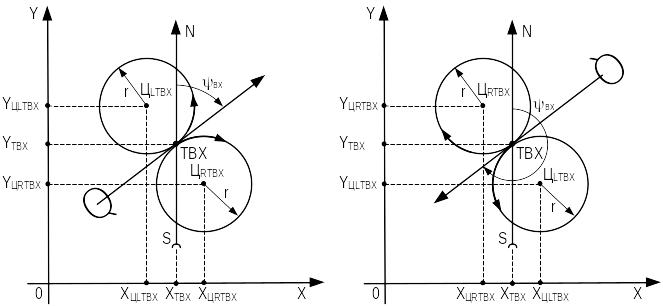
Рисунок 3.26 — Определение координат центров разворотов