3.1.5 Определение конфликтных ситуаций при непосредственном управлении воздушным движением

Представим воздушную обстановку в воздушном пространстве некоторого центра управления ВД рисунком 3.11. Воздушное судно A движется по воздушной трассе ВТ_i со скоростью V_A, воздушное судно B движется по маршруту со скоростью V_B. Воздушные суда осуществляют полёт на одном эшелоне в заданном направлении на пересекающихся курсах. Положение ВС по данным РЛС центра управления в момент времени t определяются векторами D;¯_А(t) и D;¯_B(t) текущих наклонных дальностей и азимутами ВС. Скорости и направления полёта ВС в момент времени t характеризуются векторами V;¯_А(t) и V;¯_B(t). Таким образом, в воздушном пространстве рассматриваемого центра управления ВД потенциально возможна конфликтая ситуация междувоздушными судами А и В. Определение существования ПКС требует дополнительной обработки радиолокационной информации о положении воздушных судов в момент пересечения одним из них траектории движения другого ВС.

Результатами расчёта в вычислительных устройствах РЦ, позволяющего по данным радиолокационных измерений определить наличие конфликта, является определение подлётного времени одного из ВС к точке с минимальным расстоянием между ВС (рисунок 3.11):

 .

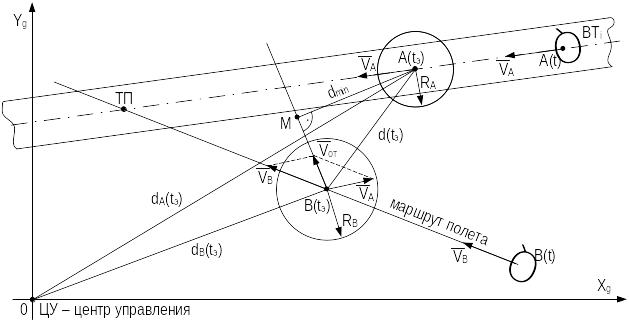
Рисунок 3.11 — Определение конфлитных ситуаций по данным радиолокационных измерений

Здесь V;¯_отн  V;¯_В  V;¯_А; d;¯  D;¯_A  D_B; S — модуль векторного произведения векторов aV;¯_отн и d;¯; L — расстояние между точкой нахождения ВС A в момент расчёта этих параметров и точкой минимального сближения двух ВС; a — коэффициент, увеличивающий модуль вектора V;¯_отн до величины L.

Расчет таких параметров конфликтной ситуации может производиться для текущего момента времени t или для экстраполированного t_э.

S  |aV;¯_отн  d;¯|  |aV;¯_отн| |d;¯| sin ,

где  — угол между векторами V;¯_отн и d;¯, при этом

aV;¯_отнd;¯  a(V;¯_BV;¯_A)(D;¯_BD;¯_A).

Разложим разности векторов по координатным осям X_g, Y_g, имеющим единичные орты i;¯ и j;¯:

(D;¯_BD;¯_A)  (D  D)i;¯  (D  D)j;¯  xi;¯  yj;¯.

Для расчёта проекций векторов V;¯_A, V;¯_B, D;¯_A и D;¯_B на координатные оси X_g и Y_g необходимо иметь значения направляющих косинусов углов ₁(V;¯_B), ₂(V;¯_A), ₃(V;¯_B), ₄(V;¯_A), ₅(V;¯_A), ₆(V;¯_B), ₇(V;¯_A) и ₈(V;¯_B) в моменты времени t или t_э.

aV;¯_отнd;¯  (aV_xi;¯  aV_yj;¯)(xi;¯  yj;¯)  a(V_xy  V_yx)k;¯;

S  |a(∆V_x∆y – ∆V_y∆x)|;

|V_отн|  ; отсюда ℓ_мин    .

Из прямоугольного треугольника следует:

L²  d²  ℓ;

d²  (∆x)²  (∆y)²;

L  ;

 

Если ℓ_min ≤ R_доп , то существует КС. R_доп — радиус зоны безопасности одного из конфликтующих ВС, в данном примере — для ВС А.

Конфликтная ситуация существует, если подлётное время находится в диапазоне   , где

 (при ℓ_min ≥ R_доп);

 (при ℓ_min < R_доп).

Таким образом, условие существования КС между конфликтующими парами <e_ВТ, e_М>:

(ℓ_min ≤ R_доп)  (  ).

Устранить конфликт можно, в принципе, путём увеличения или уменьшения модуля воздушной скорости одного из ВС, изменения курса ВС, летяшего по маршруту, и переводом любого из ВС на другие эшелоны полета. Изменение крейсерской скорости ВС в качестве маневра для устранения конфликта, как правило, не практикуется.