- •Лекция 1. Введение в цифровую обработку сигналов Введение
- •1.1. Предисловие к цифровой обработке сигналов [1i].
- •1.2. Ключевые операции цифровой обработки.
- •1.3. Области применения цифровой обработки.
- •Литература
- •Лекция 2. Цифровые фильтры обработки одномерных сигналов. Введение
- •2.1. Цифровые фильтры.
- •2.1.6. Интегрирующий рекурсивный фильтр.
- •2.2. Импульсная реакция фильтров.
- •2.3. Передаточные функции фильтров.
- •2.4. Частотные характеристики фильтров.
- •2.5. Структурные схемы цифровых фильтров.
- •Литература
- •Лекция 3. Фильтры сглаживания. Метод наименьших квадратов. Введение
- •3.1. Фильтры мнк 1-го порядка.
- •3.3. Фильтры мнк 4-го порядка.
- •3.4. Расчет простого фильтра по частотной характеристике.
- •Литература
- •Лекция 4. Разностные фильтры и фильтры интегрирования. Введение
- •4.1. Разностные операторы.
- •4.2. Интегрирование данных.
- •Литература
- •Лекция 5. Фильтрация случайных сигналов Введение
- •5.1. Фильтрация случайных сигналов.
- •5.2. Спектры мощности случайных сигналов.
- •Литература
- •Лекция 6. Весовые функции. Введение
- •3.1. Явление Гиббса.
- •3.2. Весовые функции.
- •Литература
- •Лекция 7. Нерекурсивные частотные цифровые фильтры Введение
- •7.1. Общие сведения.
- •7.2. Идеальные частотные фильтры.
- •7.3. Конечные приближения идеальных фильтров.
- •7.4. Гладкие частотные фильтры.
- •7.5. Дифференцирующие цифровые фильтры.
- •7.6. Альтернативные методы расчета нцф.
- •Литература
- •Лекция 8. Z-преобразование сигналов и системных функций Введение
- •8.2. Пространство z-полиномов.
- •8.3. Свойства z-преобразования.
- •8.4. Обратное z-преобразование.
- •8.5. Применение z – преобразования.
- •Литература
- •Лекция 9. Рекурсивные цифровые фильтры Введение
- •9.1. Принципы рекурсивной фильтрации.
- •9.2. Разработка Рекурсивных цифровых фильтров [43].
- •9.3. Режекторные и селекторные фильтры.
- •9.4. Билинейное z-преобразование.
- •9.5. Типы рекурсивных частотных фильтров.
- •Литература
- •Лекция 10. Рекурсивные частотные цифровые фильтры Введение
- •10.1. Низкочастотный фильтр Баттеруорта.
- •10.2. Высокочастотный фильтр Баттеруорта.
- •10.3. Полосовой фильтр Баттеруорта.
- •10.4. Фильтры Чебышева.
- •10.5. Дополнительные сведения.
- •Литература
- •Тема 11. Адаптивная цифровая фильтрация данных Введение
- •11.1. Общие сведения об адаптивной цифровой фильтрации.
- •11.2. Основы статистической группировки информации.
- •11.3. Статистическая регуляризация данных.
- •11.3. Статистическая группировка полезной информации.
- •Литература
- •Лекция 12. Оптимальные линейные цифровые фильтры. Введение
- •12.1. Случайные процессы и шумы.
- •12.2. Критерии построения оптимальных фильтров.
- •12.3. Фильтр Колмогорова-Винера.
- •12.4. Оптимальные фильтры сжатия сигналов.
- •12.5. Фильтр обнаружения сигналов.
- •12.6. Энергетический фильтр.
- •Литература
- •Лекция 13. Деконволюция цифровых сигналов введение
- •13.1. Понятие деконволюции.
- •13.2. Инверсия импульсного отклика фильтра.
- •13.3. Оптимальные фильтры деконволюции.
- •13.4. Рекурсивная деконволюция.
- •13.5. Фильтры сжатия сигналов
- •Литература
2.5. Структурные схемы цифровых фильтров.
Структурные схемы. Алгоритмы цифровой фильтрации сигналов (цифровых фильтров) представляются в виде структурных схем, базовые элементы которых показаны на рисунке 2.5.1 вместе с примерами структурных схем фильтров. Как правило, структурные схемы соответствуют программной реализации фильтров на ЭВМ, но не определяют аппаратной реализации в специальных радиотехнических устройствах, которая может существенно отличаться от программной реализации.
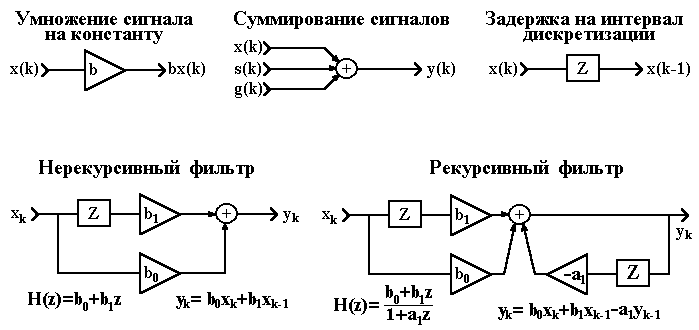
Рис. 2.5.1. Структурные схемы цифровых фильтров.
Рис. 2.5.2. Граф
фильтра.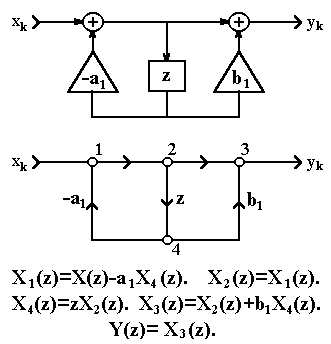
Пример структурной схемы фильтра с передаточной функцией H(z) = (1+b1z)/(1+a1z) и графа, ей соответствующего, приведен на рисунке 2.5.2. С каждым i - узлом графа связано значение сигнала xi(k) или его образа Xi(z), которые определяются суммой всех сигналов или z-образов входящих в узел ветвей. В каждой ij - ветви (из узла i в узел j) происходит преобразование сигнала в соответствии с передаточной функцией ветви, например задержка сигнала или умножение на коэффициент.
Соединения фильтров. Различают следующие соединения фильтров.
Рис. 2.5.3.![]()
Рис. 2.5.4.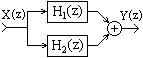
Рис. 2.5.5.
Схемы реализации фильтров. По принципам структурной реализации фильтров различают следующие схемы:
Рис. 2.5.6.
yk = bnxk-n – amyk-m,
или по передаточной функции
H(z) = bnzn /(1+ amzm).
2. Прямая каноническая форма содержит минимальное число элементов задержки. Передаточную функцию РЦФ можно представить в следующем виде:
Рис. 2.5.7.

H1(z) = V(z)/X(z) = 1/(1+ amzm),
H2(z) = Y(z)/V(z) = bnzn.
Отсюда: v(k) = x(k) - amv(k-m), (2.5.1)
y(k) = bnv(k-n). (2.5.2)
В разностных уравнениях (2.5.1-2.5.2) осуществляется только задержка сигналов v(k). Граф реализации РЦФ в прямой канонической форме приведен на рисунке 2.5.7.
3. Каскадная (последовательная) форма соответствует представлению передаточной функции в виде произведения:
H(z) =![]() Hi(z).
Hi(z).
Hi(z) - составляющие функции вида (1-riz)/(1-piz) при представлении H(z) в факторизованной форме, где ri и pi - нули и полюсы функции H(z). В качестве функций Hi(z) обычно используются передаточные функции биквадратных блоков - фильтров второго порядка:
Hi(z) = (b0i + b1i z + b2i z2) / (1 + a1i z + a2i z2).
4. Параллельная форма используется много реже, и соответствует представлению передаточной функции в виде суммы биквадратных блоков или более простых функций.
Рис. 2.5.8.