
ФИНАНСОВЫЙ АНАЛИЗ В EXCEL
EXCEL предоставляет большой спектр функций финансового анализа: от нахождения платы по процентам, амортизации оборудования, регулярных выплат по займу до оценки эффективности капитальных вложений. В этих заданиях мы на конкретных примерах рассмотрим функции финансового анализа EXCEL.
Задание № 1
Описание функции ПЛТ или ППЛАТ (ставка ;кпер;пс;бс;тип)
Возвращает сумму периодического платежа на основе постоянства сумм платежей и постоянства процентной ставки.
ставка — процентная ставка по ссуде.
кпер — общее число выплат по ссуде.
пс — приведенная к текущему моменту стоимость, или общая сумма, которая на
текущий момент равноценна ряду будущих платежей, называемая также основной
суммой.
бс — требуемое значение будущей стоимости, или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (нулю), т. е. для займа, например, значение бс равно 0.
тип — число 0 (нуль) или 1, обозначающее, когда должна производиться выплата.
Пример
A |
B |
Данные |
Описание |
8% |
Годовая процентная ставка |
10 |
Количество месяцев платежей |
10000 |
Сумма кредита |
Формула |
Описание (результат) |
=ПЛТ(A2/12; A3; A4) |
Месячная сумма платежа по указанному кредиту (-1 037,03) |
=ПЛТ(A2/12; A3; A4; 0; 1) |
Месячная сумма платежа по указанному кредиту, исключая платежи, производимые в начале периода (-1 030,16) |
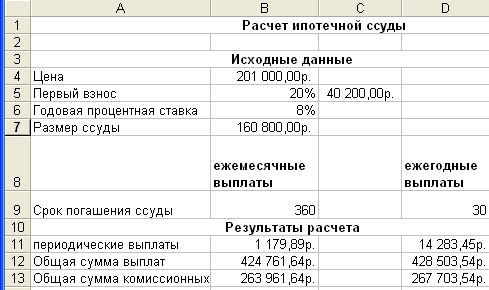
Рассмотрим пример расчета 30-летней ипотечной ссуды со ставкой 8% годовых при начальном взносе 20% и ежемесячной (ежегодной) выплате с помощью функции ППЛАТ
(ПЛТ).
Функция ППЛАТ (ПЛТ) вычисляет величину постоянной периодической выплаты ренты (например, регулярных платежей по займу) при постоянной процентной ставке.
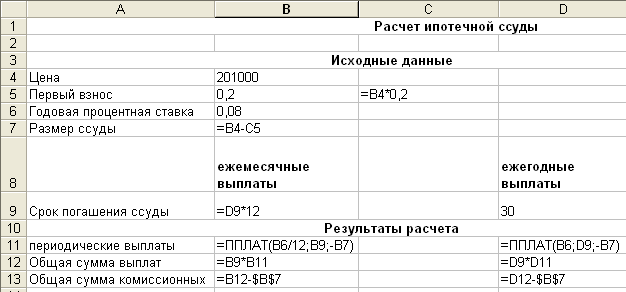
Отметим, что очень важно быть последовательным в выборе единиц измерения для задания аргументов СТАВКА и КПЕР. Например, если вы делаете ежемесячные выплаты по четырехгодичному займу из расчета 12% годовых, то для задания аргумента СТАВКА используйте 12%/12, а для задания аргумента КПЕР – 4*12. Если вы делаете ежегодные платежи по тому же займу, то для задания аргумента СТАВКА используйте 12%, а для задания аргумента КПЕР – 4.
Для нахождения общей суммы, выплачиваемой на протяжении интервала выплат, умножьте возвращаемое функцией ППЛАТ значение на величину КПЕР. Интервал выплат – это последовательность постоянных денежных платежей, осуществляемых за непрерывный период.
В функциях, связанных с интервалами выплат, выплачиваемые вами деньги, такие как депозит на накопление, представляются отрицательным числом, а деньги, которые вы получаете, такие как чеки на дивиденды, представляются положительным числом.
Например, депозит в банк на сумму 1000 рублей представляются аргументом –1000, если вы вкладчик, и аргументом 1000, если вы представитель банка.
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ. Вычислить n-годичную (общее число периодов выплат) ипотечную ссуду покупки квартиры за Р руб. с годовой ставкой i % и начальным взносом A%, . Cделать расчет для ежемесячных и ежегодных выплат. Найти суммы периодических ежемесячных и ежегодных выплат, общие суммы ежемесячных и ежегодных выплат, общие суммы ежемесячных и ежегодных комиссионных.
Для выполнения задания заполните таблицу своими исходными данными:
Стоимость квартиры - Р
Годовая ставка i%
Срок погашения ссуды n
Начальный взнос A%
Начальный взнос в денежном выражении рассчитывается по формуле:
стоимость квартиры*А%
Ежегодные выплаты рассчитываются по функции
(ПЛТ(ставка ;кпер;пс;бс;тип) либо ППЛАТ(ставка;срок;-ссуда);
ежемесячные выплаты
ППЛАТ(ставка/12;срок*12;-ссуда)), либо ПЛТ(ставка/12;срок*12;-ссуда)
где ссуда (пс) - текущее значение, т.е. общая сумма, которую составят будущие платежи (в нашем примере – это разность между стоимостью квартиры и начальным взносом).
Общие ежемесячные = ежемесячные*срок*12
Общие ежегодные = ежегодные*срок
Ежемесячные комиссионные = общие ежемесячные - ссуда
Ежегодные комиссионные = общие ежегодные – ссуда
Варианты заданий
Вариант |
n |
P |
i |
A |
1 |
9 |
270000 |
5 |
10 |
2 |
7 |
200500 |
6 |
12 |
3 |
8 |
220600 |
7 |
11 |
4 |
10 |
300700 |
8 |
22 |
5 |
9 |
350800 |
9 |
17 |
6 |
7 |
210700 |
6 |
12 |
7 |
8 |
250900 |
11 |
32 |
8 |
9 |
310500 |
12 |
31 |
9 |
10 |
320600 |
13 |
27 |
10 |
11 |
360400 |
14 |
23 |
11 |
5 |
150200 |
5 |
10 |
12 |
6 |
160500 |
6 |
12 |
13 |
7 |
180200 |
7 |
19 |
14 |
8 |
190100 |
12 |
16 |
15 |
9 |
230100 |
9 |
29 |
16 |
10 |
240300 |
10 |
27 |
17 |
11 |
260900 |
5 |
28 |
18 |
12 |
270500 |
6 |
18 |
19 |
6 |
280700 |
7 |
10 |
20 |
7 |
290300 |
8 |
19 |
21 |
5 |
330300 |
9 |
12 |
22 |
10 |
300700 |
8 |
22 |
23 |
7 |
180200 |
7 |
19 |
24 |
8 |
190100 |
12 |
16 |
25 |
9 |
230100 |
9 |
29 |
26 |
10 |
240300 |
10 |
27 |
Задание №2
ЧПС(ставка ;значение1;значение2; ...) или НПЗ (ставка ;значение1;значение2; ...)
Возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также стоимости будущих выплат (отрицательные значения) и поступлений (положительные значения).
ставка — ставка дисконтирования за один период.
Значение1, значение2,... — от 1 до 29 аргументов, представляющих расходы и доходы.
Значение1, значение2, ... должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.
ЧПС использует порядок аргументов значение1, значение2, ... для определения порядка поступлений и платежей. Убедитесь в том, что ваши платежи и поступления введены в правильном порядке.
Пример 1
A |
B |
Данные |
Описание |
10% |
Годовая ставка дисконтирования |
-10 000 |
Начальные затраты на инвестиции за один год, считая от текущего момента |
3 000 |
Доход за первый год |
4 200 |
Доход за второй год |
6 800 |
Доход за третий год |
Формула |
Описание (результат) |
=ЧПС(A2; A3; A4; A5; A6) |
Чистая приведенная стоимость инвестиции (1 188,44) |
В примере начальные затраты в 10 000 руб. были включены как одно из значений, поскольку выплата производилась в конце первого периода.
Пример 2
|
В этом примере начальные затраты в 40 000 руб. не были включены как одно из значений, поскольку выплата производилась в начале первого периода.
Рассмотрим следующую задачу. Вас просят дать в долг 10 000 рублей и обещают вернуть через год 2 000 рублей, через два года – 4 000 рублей. Через три года – 7 000 рублей. При какой годовой процентной ставке эта сделка выгодна?
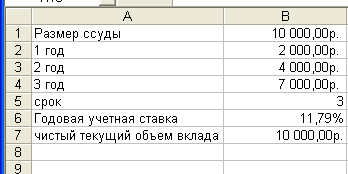
В приводимом расчете в ячейку в ячейку В7 введена формула
=НПЗ (В6;В2:В4)
Первоначально в ячейку В6 вводится произвольный процент, например 3%. После этого выбираем команду Сервиз, Подбор параметра и заполняем открывшееся диалоговое окно Подбор параметра.
В поле Установить в ячейке даем ссылку на ячейку В7, в которой вычисляется чистый текущий объем вклада по формуле
=НПЗ (В6;В2:В4)
В поле Значение указываем 10000 – размер ссуды. В поле Изменяя значение ячейки даем ссылку на ячейку В6, в которой вычисляется годовая процентная ставка. После нажатия кнопки ОК средство подбора параметров определит, при какой годовой процентной ставке чистый текущий объем вклада равен 10000 рублей. Результат вычисления выводится в ячейку В6.
В нашем случае годовая учетная ставка равна 11,79%.
Вывод: если банки предлагают большую годовую процентную ставку, то предлагаемая сделка не выгодна.
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ: Вас просят дать в долг Р рублей и обещают вернуть Р1 руб. через год, Р2 руб. – через два года и т.д. и, наконец, РН руб. через Н лет. При какой годовой процентной ставке эта сделка имеет смысл? (ЧПС(ставка ; значение1;значение2; ...). Для уточнения процентной ставки использовать метод подбора параметра.
Вариант |
Н |
Р |
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
1 |
5 |
37000 |
5000 |
7000 |
8000 |
9000 |
11000 |
2 |
4 |
20700 |
6000 |
6000 |
9000 |
7000 |
|
3 |
3 |
20000 |
5000 |
8000 |
8000 |
|
|
4 |
5 |
30700 |
5000 |
10000 |
18000 |
2000 |
3000 |
5 |
4 |
45000 |
12000 |
9000 |
10000 |
18000 |
|
6 |
5 |
21900 |
4000 |
5000 |
8000 |
10600 |
11000 |
7 |
5 |
32500 |
8000 |
9000 |
10000 |
3070 |
2000 |
8 |
4 |
31200 |
9000 |
10000 |
10000 |
15000 |
|
9 |
3 |
32000 |
15000 |
10000 |
10000 |
|
|
10 |
3 |
36600 |
10700 |
15000 |
21000 |
|
|
11 |
4 |
18000 |
4000 |
6000 |
9800 |
5500 |
|
12 |
5 |
16300 |
5000 |
6000 |
7050 |
800 |
400 |
13 |
3 |
18500 |
8500 |
4700 |
6000 |
|
|
14 |
4 |
19500 |
10200 |
5000 |
7000 |
3000 |
|
15 |
5 |
23800 |
9000 |
8000 |
6060 |
5000 |
4000 |
16 |
3 |
24300 |
9600 |
10000 |
7000 |
|
|
17 |
4 |
26900 |
7000 |
5000 |
7020 |
8000 |
|
18 |
3 |
27000 |
15000 |
8000 |
6000 |
|
|
19 |
3 |
28050 |
8000 |
10000 |
11050 |
|
|
20 |
5 |
29500 |
9000 |
7000 |
8050 |
7000 |
2300 |
21 |
4 |
33800 |
8000 |
7000 |
10000 |
9030 |
|
22 |
4 |
20700 |
6000 |
6000 |
9000 |
7000 |
|
23 |
5 |
30700 |
5000 |
10000 |
18000 |
2000 |
3000 |
24 |
5 |
21900 |
4000 |
5000 |
8000 |
10600 |
11000 |
25 |
4 |
19500 |
10200 |
5000 |
7000 |
3000 |
|
26 |
3 |
27000 |
15000 |
8000 |
6000 |
|
|
