9.4.2. Доверительный интервал для оценки математического ожидания нормального распределения при неизвестной дисперсии

Однако на практике почти всегда дисперсия неизвестна. Если известно, что исследуемая случайная величина Х распределена по нормальному закону с неизвестным средним квадратическим отклонением, то для поиска доверительного интервала для ее математического ожидания заменим дисперсию ее «наилучшей» оценкой по выборке, т.е. «исправленной» дисперсией , и построим новую случайную величину

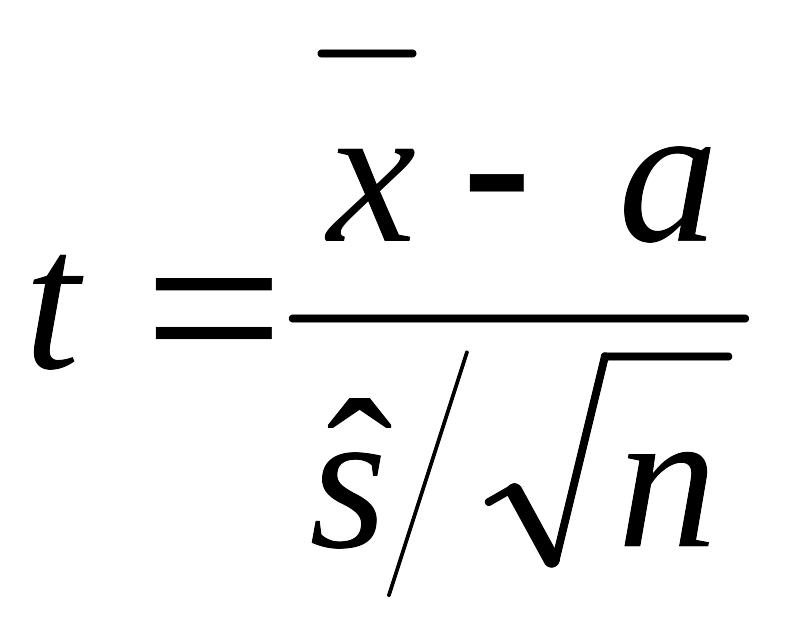
где – выборочное среднее, – исправленная дисперсия, п – объем выборки.

Представим эту случайную величину в виде

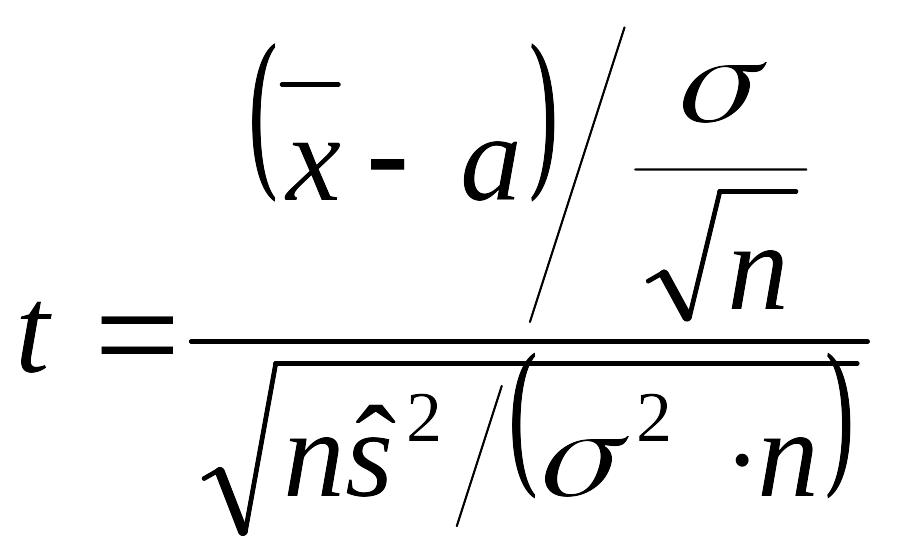
Числитель этого выражения имеет стандартное нормальное распределение N(0, 1). Случайная величина имеет χ² –распределение с k=n–1 степенями свободы. Следовательно, статистика t имеет t –распределение Стьюдента с k=n–1 степенями свободы. Указанное распределение не зависит от неизвестных параметров распределения, а зависит лишь от числа k.

Зная t –распределение Стьюдента, можно найти критическое значение , что вероятность того, что статистика не превзойдет величину по абсолютной величине:

.

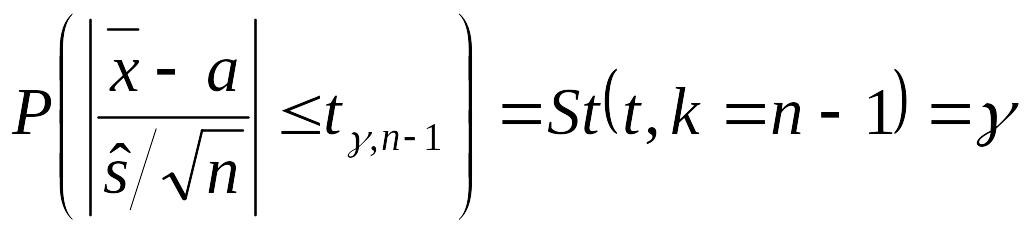Отсюда получаем:

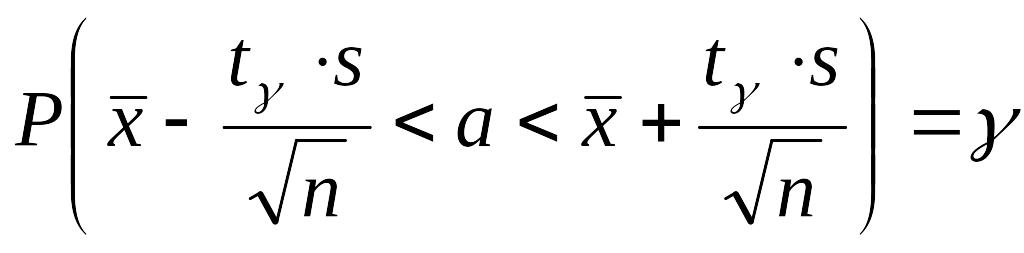
Таким образом, получен доверительный интервал для а, где t_g можно найти по соответствующей таблице при заданных п и g.

Пример. Пусть объем выборки . Найти доверительный интервал для а при g = 0,99.

Решение.

Из таблицы находим, что . Тогда

.

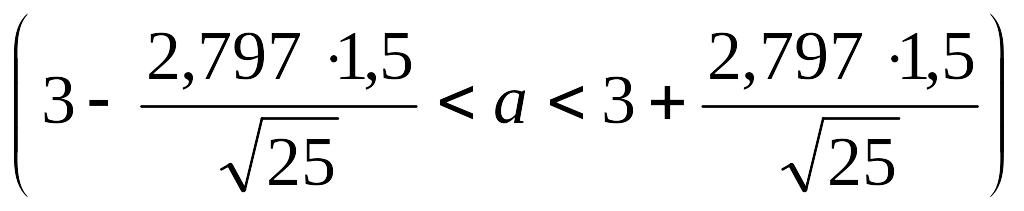Таким образом, доверительный интервал, в который попадает а с надежностью 0,99 имеет вид: .

9.4.3. Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения

Будем искать для среднего квадратического отклонения нормально распределенной случайной величины доверительный интервал вида ( ), где – исправленное выборочное среднее квадратическое отклонение, а для δ выполняется условие: . Запишем это неравенство в виде:

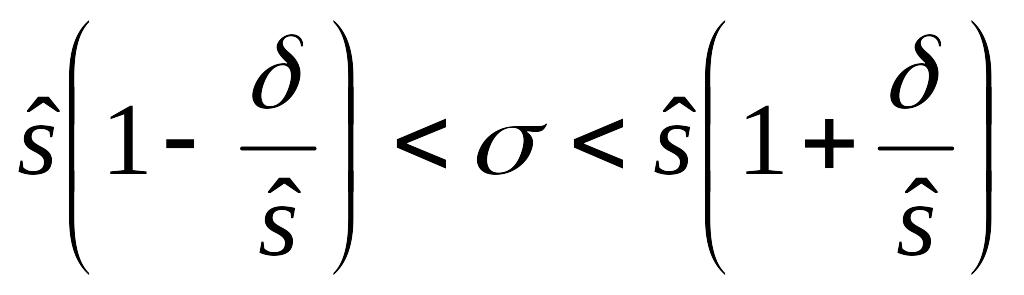
или, обозначив

.

Рассмотрим случайную величину c, определяемую по формуле

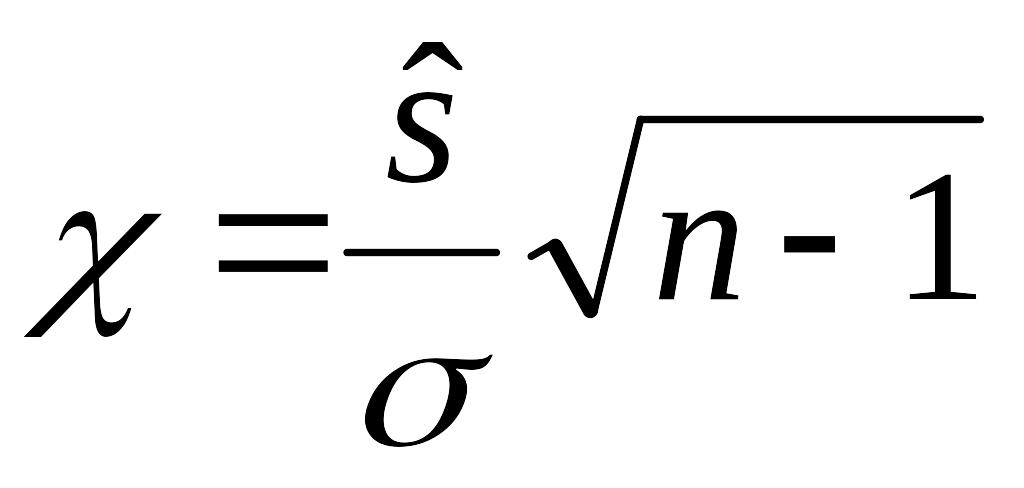или

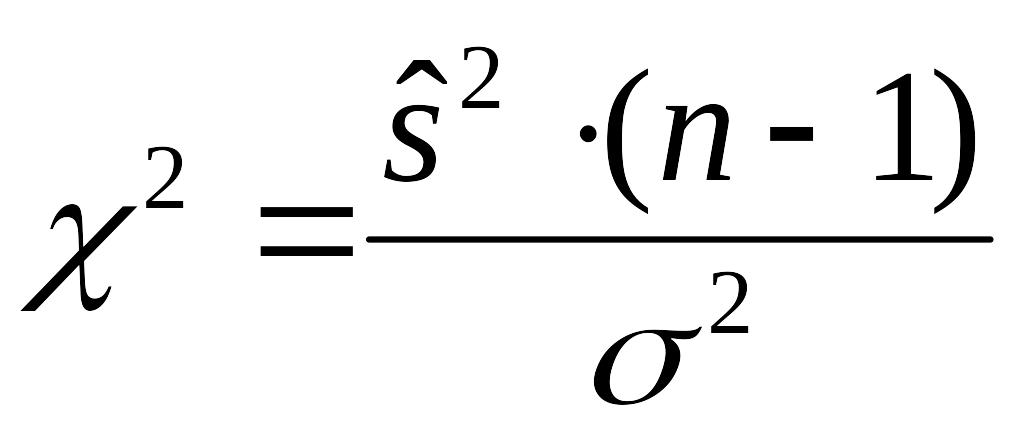
которая распределена по закону «хи-квадрат» с п–1 степенями свободы.

Предположим, что , тогда неравенство

можно записать так: ,

или, после умножения на

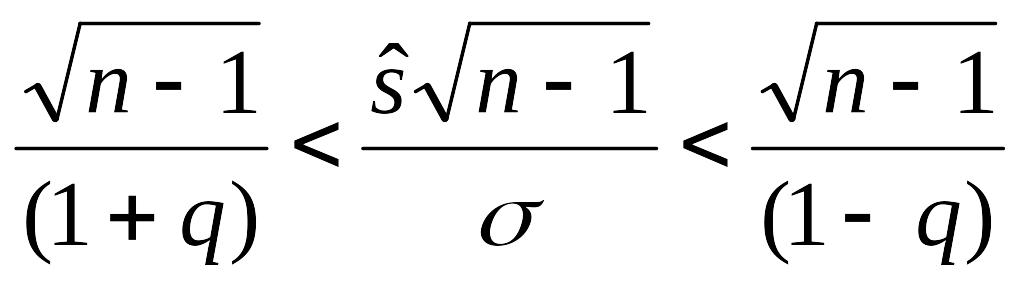
Следовательно, .

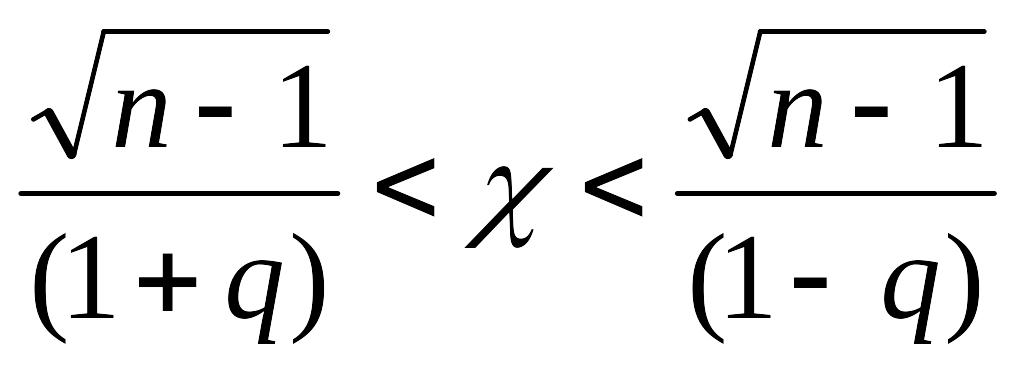Существуют таблицы для распределения «хи-квадрат», из которых можно найти q по заданным п и g. Таким образом, вычислив по выборке значение и определив по таблице значение q, можно найти доверительный интервал, в который значение s попадает с заданной вероятностью g.

Замечание. Если q > 1, то с учетом условия s > 0 доверительный интервал для s будет иметь границы

Пример. Пусть . Найдем доверительный интервал для s при заданной надежности g = 0,95.

Решение.

Из соответствующей таблицы находим q(n=20, g=0,95)=0,37. Следовательно, границы доверительного интервала:

. Итак, .

9.4.4. Доверительный интервал для вероятности

Найдем доверительный интервал для оценки вероятности по относительной частоте.

Вероятность того, что абсолютная величина отклонения не превысит положительного числа :

, где .

Заменив в этом соотношении случайную величину и ее математическое ожидание а соответственно случайной величиной w и ее математическим ожиданием р, получим приближенное (так как относительная частота распределена приближенно нормально) равенство

, где ,

Тогда и доверительный интервал для вероятности р находим из условия

.

Возведя обе части неравенства в квадрат, преобразуем его

или равносильное квадратное уравнение

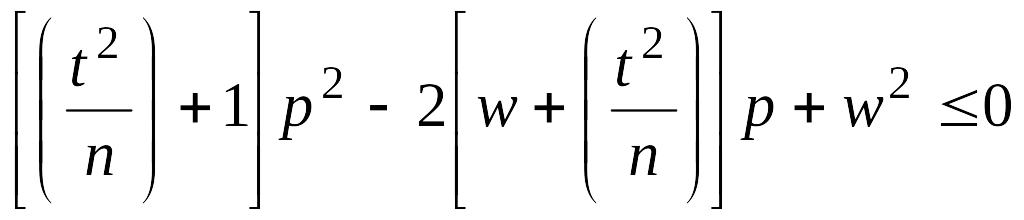
Дискриминант трехчлена положительный , поэтому корни действительные и различные. Границы (р₁; р₂) доверительного интервала находятся по формуле

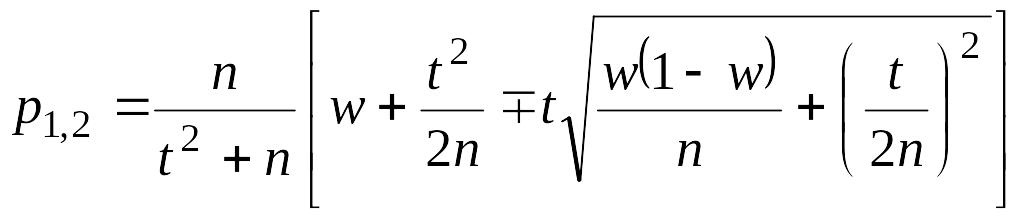
В случае больших выборок величиной (по сравнению с w), (по сравнению с w(1– w)/n) можно пренебречь, и получим

.

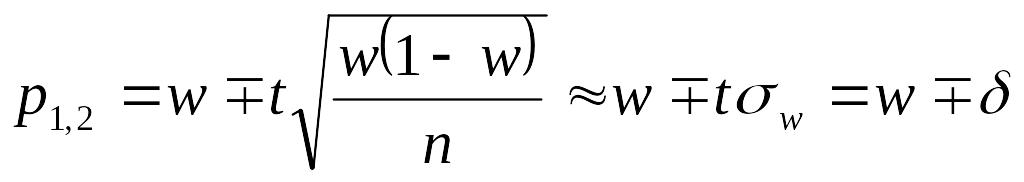Пример. Производят независимые испытания с одинаковой, но неизвестной вероятностью р появления события А в каждом испытании. Найти доверительный интервал для оценки вероятности р с надежностью , если в 80 испытаниях событие А появилось 16 раз.

Решение.

По условию, . Найдем относительную частоту появления события А: . Найдем t из соотношения ; по таблице функции Лапласа находим . Границы (р₁; р₂) доверительного интервала находятся по формуле

получим соответственно

.

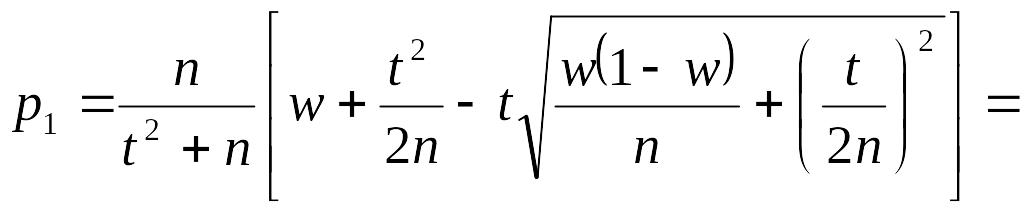
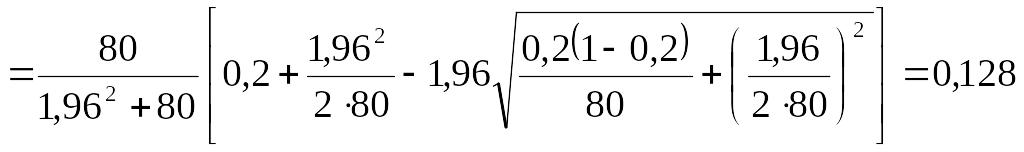
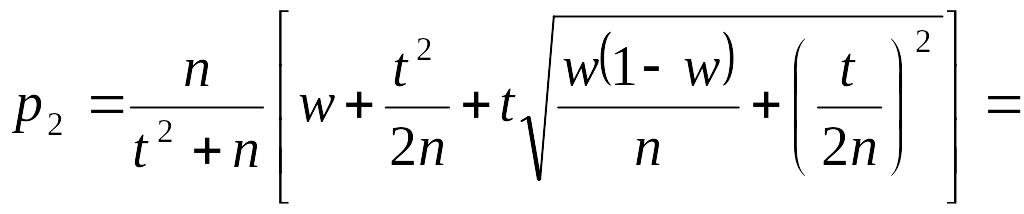
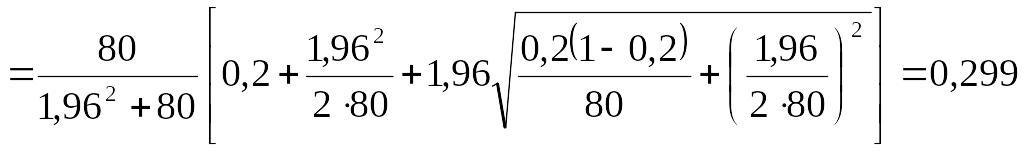Итак, искомый доверительный интервал .

25