9.2.3. Метод наименьших квадратов (мнк)

Это один из наиболее простых методов построения оценок. Суть его заключается в том, что оценка определяется из условия минимизации суммы квадратов отклонений выборочных данных от определенной оценки

Пример. Найти оценку метода наименьших квадратов МНК для генеральной средней .

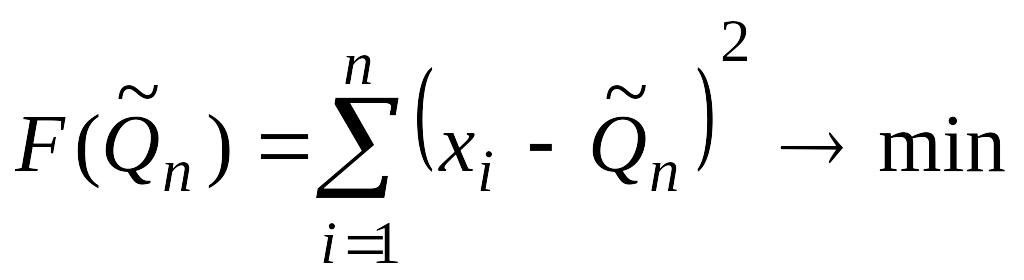
Решение.

Используя необходимое условие экстремума, приравниваем нулю производную

,

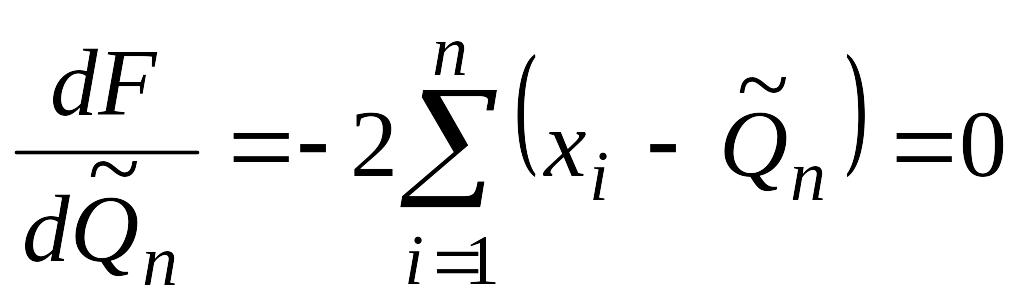тогда

,

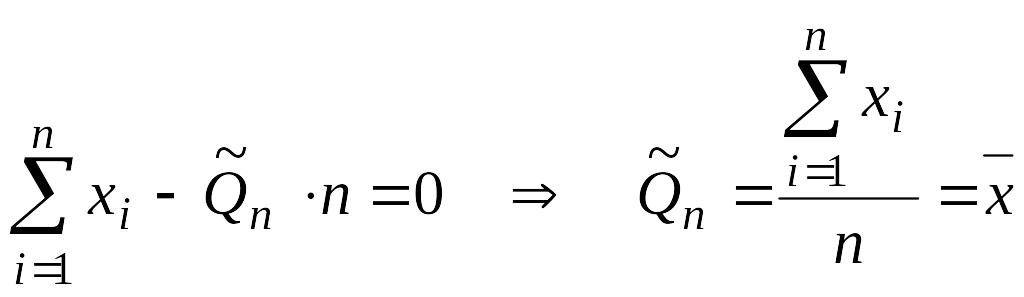т.е. искомая оценка генеральной средней есть выборочная средняя .

МНК получил самое широкое распространение в практике статистических исследований, т.к. не требует знания закона распределения выборочных данных и при этом достаточно хорошо разработан в плане вычислений.

9.3. Интервальная оценка параметров распределения

При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, что приводит к грубым ошибкам. Интервальная оценка характеризуется двумя числами – концами интервала , внутри которого предположительно находится истинное значение параметра θ, т.е., вместо отдельной точки для оцениваемого параметра можно установить интервал значений, одна из точек которого является «лучшей» оценкой. Интервальные оценки являются более полными и надежными по сравнению с точечными, они применяются как для больших, так и для малых выборок.

Интервальной оценкой параметра θ называется числовой интервал , который с заданной вероятностью γ накрывает неизвестное значение параметра θ.

Интервал называется доверительным, а вероятность γ – доверительной вероятностью или надежностью (вероятность, с которой выполняется неравенство ).

Очень часто доверительный интервал выбирается симметричным относительно параметра θ: .

Величины и называются нижней и верхней доверительными границами. Доверительные границы интервала выбирают так, чтобы выполнялось условие .

Число ∆ называется точностью оценки или ошибкой репрезентативности (представительства) выборки (она возникает из-за того, что исследуется не вся совокупность, а лишь ее часть).

Величина доверительного интервала и его границы существенно зависит от объема выборки и от значения доверительной вероятности γ.

Задачей интервального оценивания параметров: определение интервала, а не единичного значения, в котором с заданной степенью достоверности (доверительной вероятностью ) будет заключено значение оцениваемого параметра.

Обычно надежность оценки задается наперед, причем в качестве берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999. Тогда событие, состоящее в том, что интервал [ , ] накрывает параметр, будет практически достоверным. Также практически достоверным является событие, состоящее в том, что погрешность оценки не меньше ∆, или точность оценки больше ∆. Нахождение доверительных интервалов требует знания вида и параметров закона распределения случайной величины θ. Для ряда практически важных случаев этот закон можно определить из теоретических соображений.

9.4. Построение доверительных интервалов

9.4.1. Доверительный интервал для оценки математического ожидания нормального распределения при известной дисперсии

Пусть исследуемая случайная величина Х распределена по нормальному закону с известным средним квадратическим s, и требуется по значению выборочного среднего оценить ее математическое ожидание а. Будем рассматривать выборочное среднее как случайную величину , а значения вариант выборки х₁, х₂,…, х_п – как одинаково распределенные независимые случайные величины Х₁, Х₂,…, Х_п, каждая из которых имеет математическое ожидание а и среднее квадратическое отклонение s. При этом

,

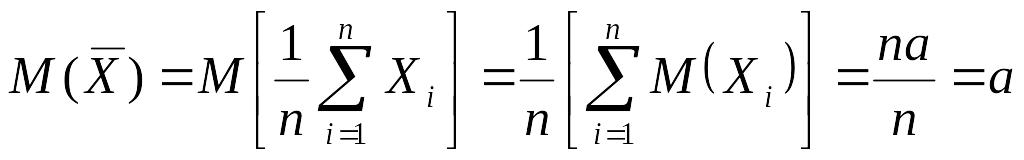и

.

(используем свойства математического ожидания и дисперсии суммы независимых случайных величин). Оценим вероятность выполнения неравенства

.

Применим формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал:

Тогда, с учетом того, что

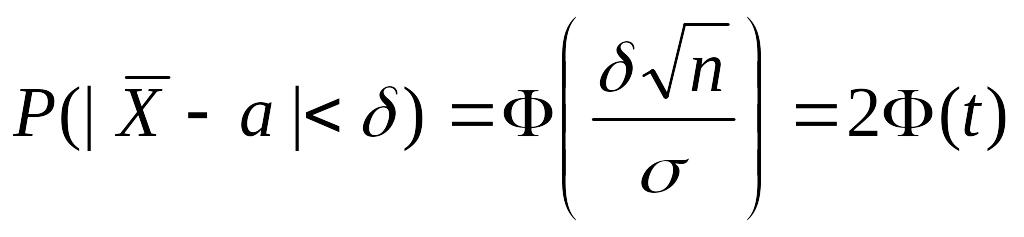, где .

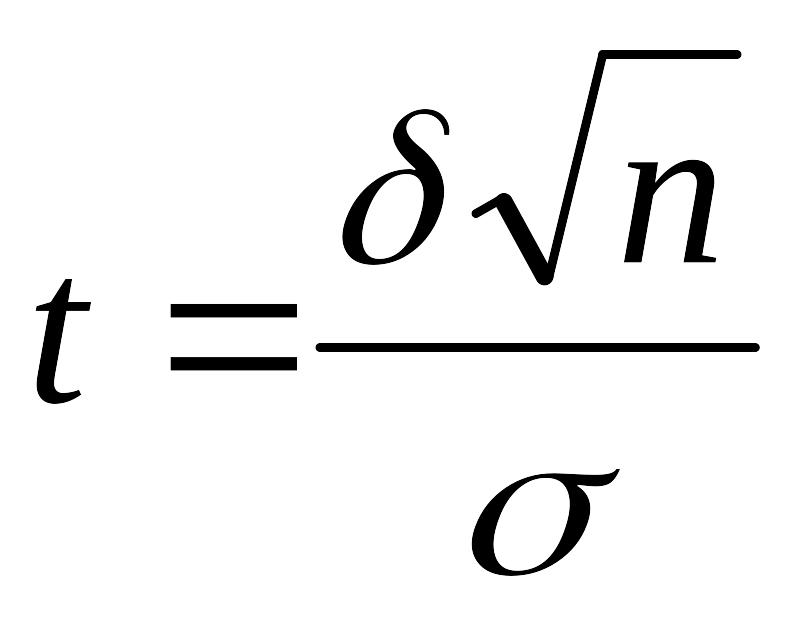Отсюда 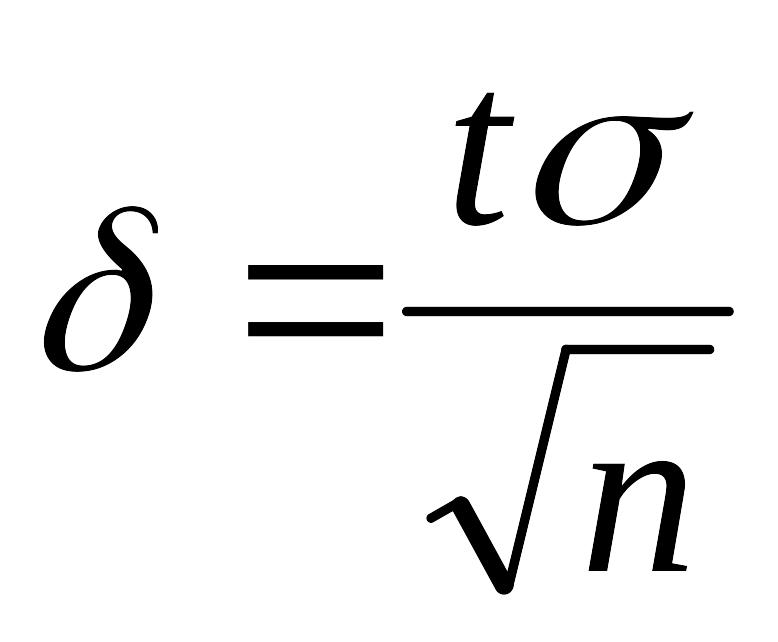. Следовательно, предыдущее равенство можно переписать:

.

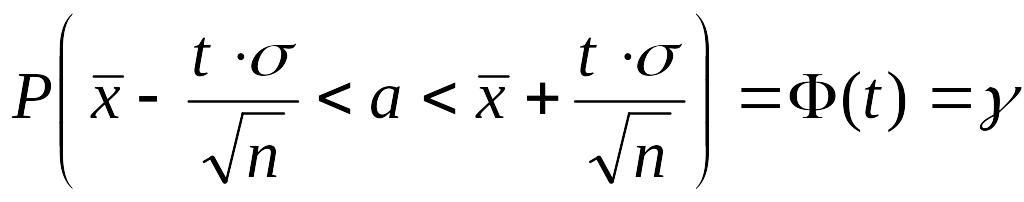Итак, значение математического ожидания а с вероятностью (надежностью) g попадает в интервал

,

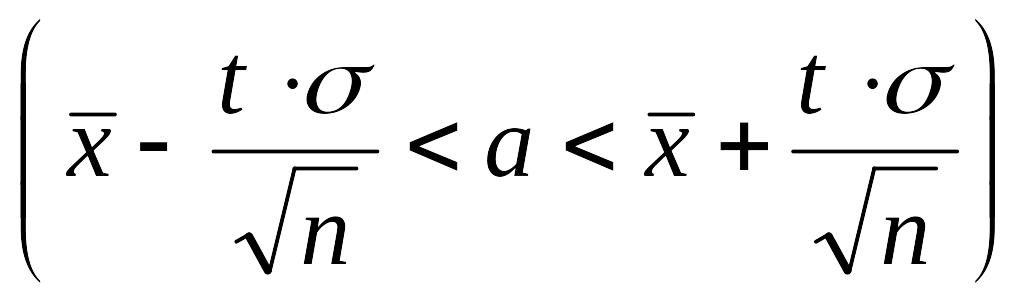где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство Ф(t) = g.

Пример. Найти доверительный интервал для математического ожидания нормально распределенной случайной величины, если объем выборки , а доверительная вероятность g = 0,9.

Решение.

Определим t, при котором : . Тогда

.

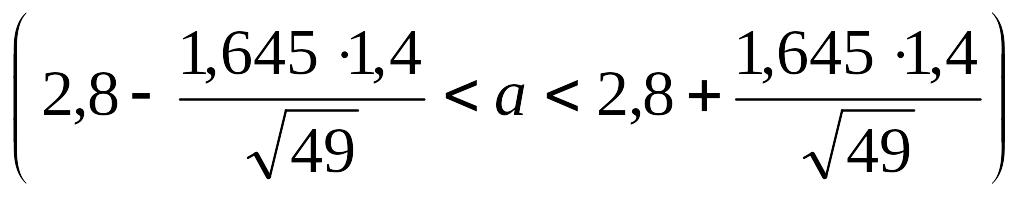Таким образом, доверительный интервал, в который попадает а с надежностью 0,9 имеет вид: .