9.1.3. Частость как точечная оценка вероятности события

Обозначим через р неизвестную вероятность появления события А в единичном испытании. Найдем приближенное значение w вероятности р. Проведем n независимых испытаний по схеме Бернулли. Пусть m – количество испытаний, в которых произошло событие А. Тогда w= m/ n – это частость появления события А. выясним, какими свойствами обладает w как точечная оценка вероятности р события.

Теорема. Пусть m – число наступлений события А в n независимых испытаниях, р - вероятность наступления события А в каждом из испытаний. Тогда w= m/ n – состоятельная, несмещенная и эффективная оценка вероятности р.

Состоятельность.

Для испытаний по схеме Бернулли справедлива теорема Бернулли, согласно которой для любого ε>0 имеет место равенство

.

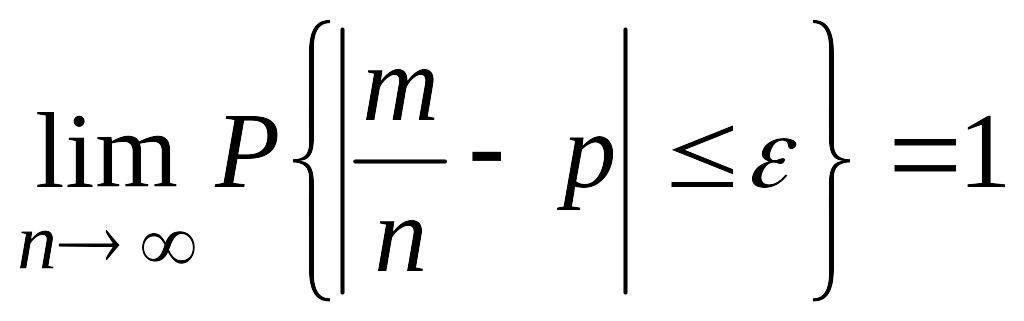Из определения состоятельности следует, что если , а , то w= m/n – состоятельная оценка вероятности р.

Несмещенность

Найдем математическое ожидание частости:

.

Таким образом, при любом фиксированном числе n испытаний . Это означает, что w= m/ n является несмещенной оценкой вероятности р.

Эффективность.

Сопоставим с результатом единичного испытания случайную величину

Х	xi	0	1
	рi	q	р

Последовательность n испытаний по схеме Бернулли – это n независимых наблюдений случайной величины Х, проводимых в одинаковых условиях, тогда нижняя граница для дисперсий различных несмещенных оценок вероятности р равна р(р-1)/n.

Теперь найдем дисперсию частости:

_.

Так как совпадает с минимальной границей, то w= m/ n является несмещенной и эффективной оценкой вероятности р.

9.2. Методы оценки параметров распределения

Существует несколько методов нахождения точечной оценки параметров, наиболее употребительными из них являются методы максимального (наибольшего) правдоподобия, моментов и метод наименьших квадратов.

9.2.1. Метод максимального правдоподобия (ммп)

Метод предложен Р. Фишером в 1912г. Основу метода составляет функция правдоподобия как функция параметра θ, выражающая вероятность (плотность) совместного появления результатов выборки наблюдений x₁, x₂, …, x_n.

L(х₁, х₂ …, х_n ; θ) = p(х₁, θ) p(х₂, θ) … p(х_п, θ)

или

L(х₁, х₂ …, х_n ; θ) = f(х₁, θ) f(х₂, θ) … f(х_п, θ).

Тогда в качестве точечной оценки параметра θ принимают такое его значение

=θ(х₁, х₂, …, х_п),

при котором функция правдоподобия достигает максимума. Оценку называют оценкой наибольшего правдоподобия.

В качестве оценки неизвестного параметра следует взять такое значение , которое обращает функцию правдоподобия в максимум.

Пусть Х – дискретная случайная величина, которая в результате п испытаний приняла значения х₁, х₂, …, х_п. Предположим, что нам известен закон распределения этой величины, определяемый параметром θ, но неизвестно численное значение этого параметра. Найдем его точечную оценку.

Поскольку функции L и lnL достигают максимума при одном и том же значении θ, удобнее искать максимум ln L – логарифмической функции правдоподобия. Для этого нужно:

1. найти производную ;

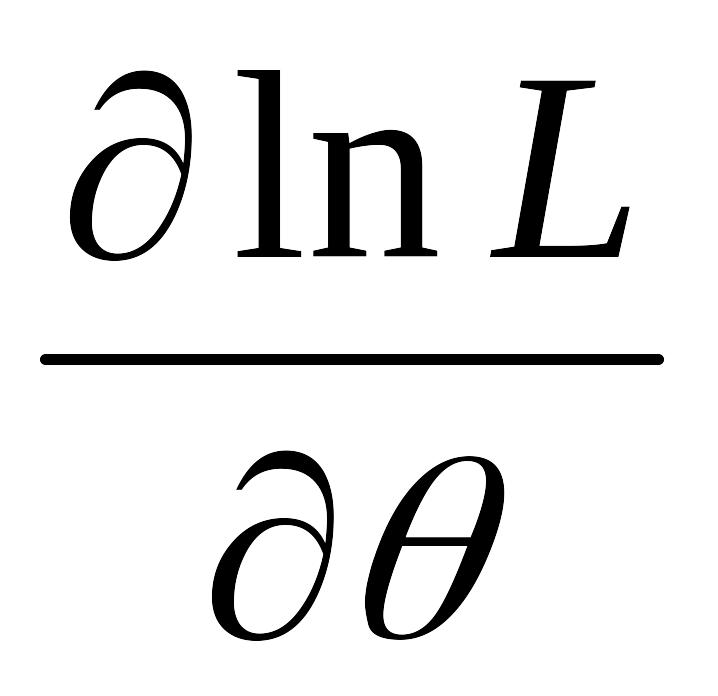2. приравнять ее нулю (получим так называемое уравнение правдоподобия) и найти критическую точку;

3. найти вторую производную 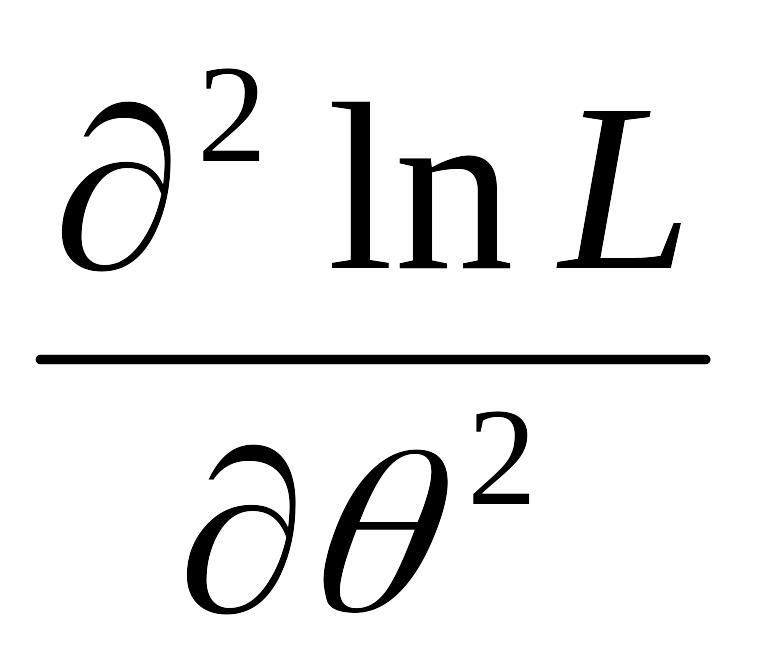, если она отрицательна в критической точке, то это – точка максимума.

Достоинства метода наибольшего правдоподобия: полученные оценки состоятельны (хотя могут быть смещенными), распределены асимптотически нормально при больших значениях п и имеют наименьшую дисперсию по сравнению с другими асимптотически нормальными оценками; если для оцениваемого параметра θ существует эффективная оценка , то уравнение правдоподобия имеет единственное решение ; метод наиболее полно использует данные выборки и поэтому особенно полезен в случае малых выборок.

Недостаток метода наибольшего правдоподобия: сложность вычислений.

Пример. Будем считать, что случайная величина Х, имеет нормальное распределение с плотностью вероятности

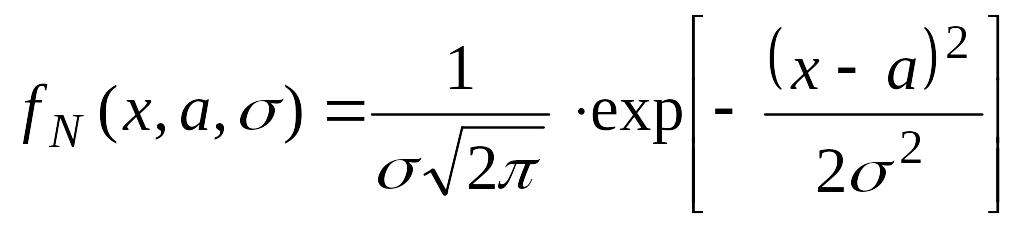
По выборке значений найдены фактические значения оценок математического ожидания и дисперсии: =27,51, s² = 0,91.

Необходимо найти оценки максимального правдоподобия параметров а и ² этого распределения.

Решение. Функция правдоподобия для выборки ЭД объемом n

.

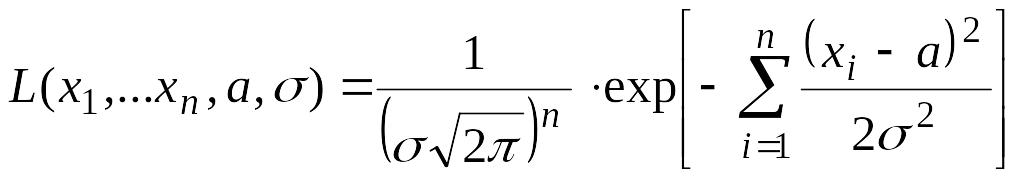Логарифм функции правдоподобия

.

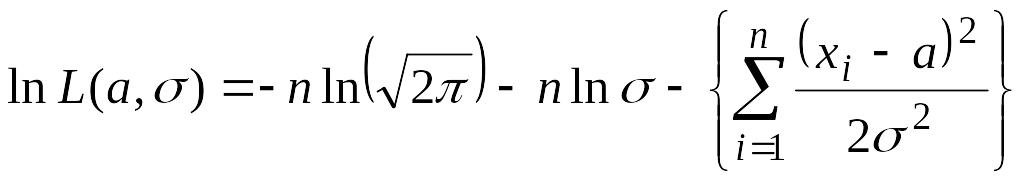Система уравнений для нахождения оценок параметров

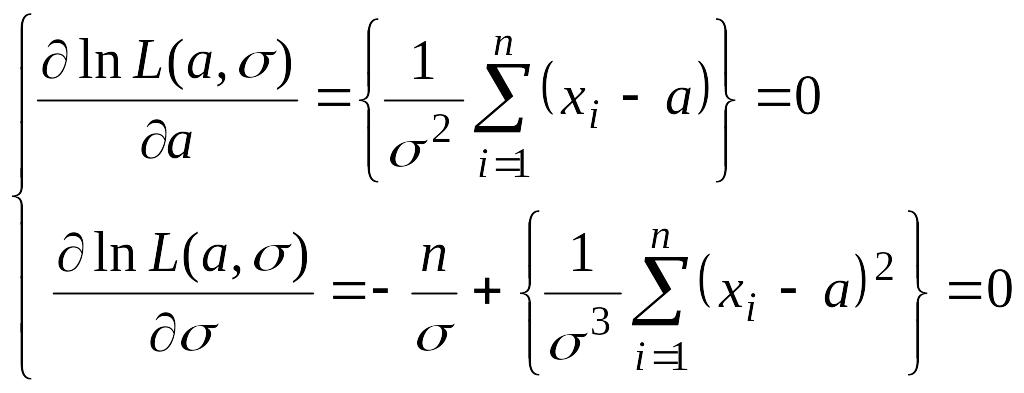
Из первого уравнения следует:

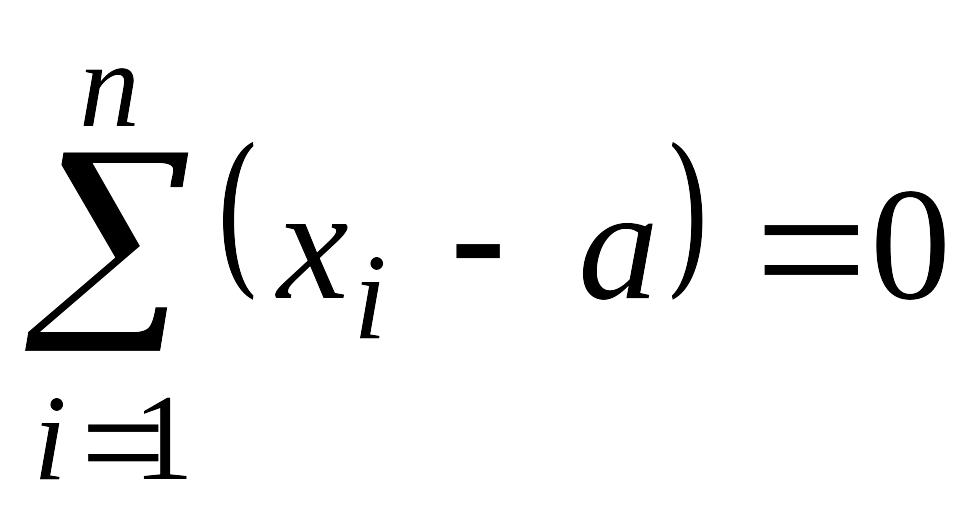и ,

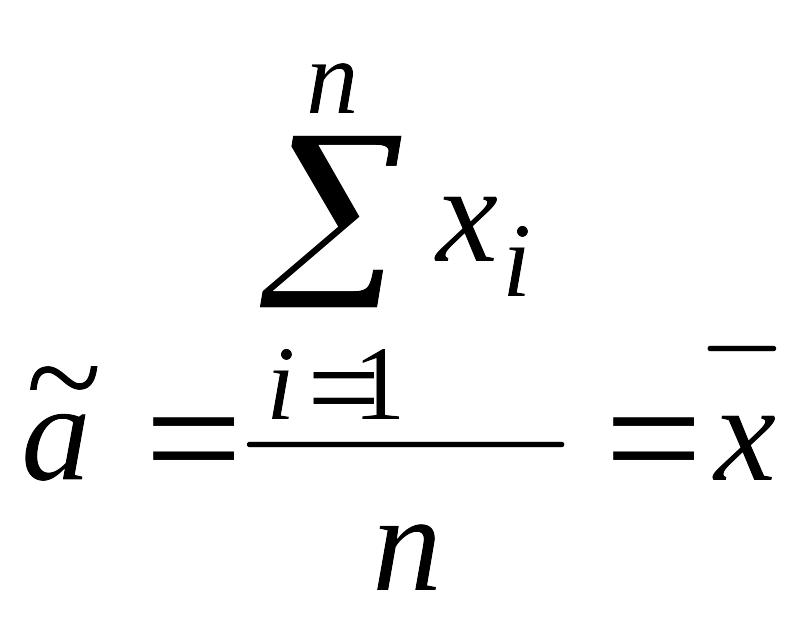т.е. среднее арифметическое является оценкой максимального правдоподобия для математического ожидания. Из второго уравнения можно найти

,

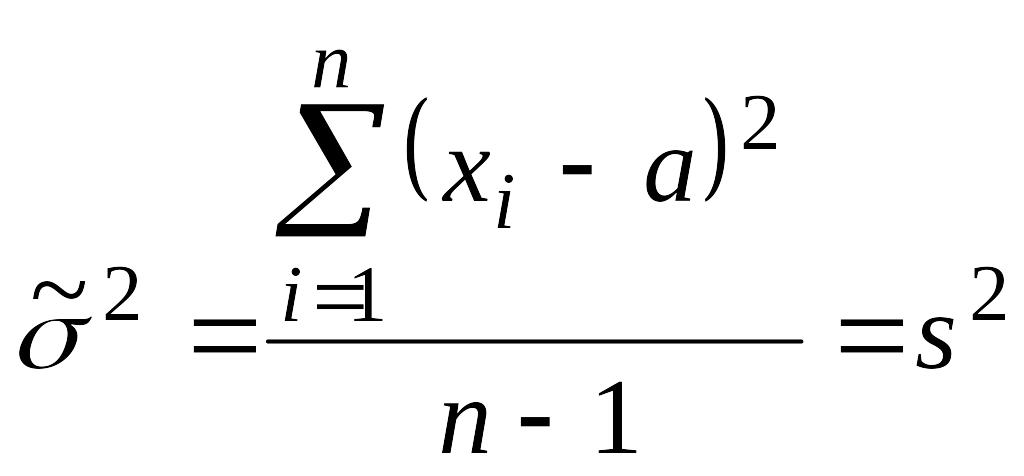т.е. оценку максимального правдоподобия для дисперсии – выборочную дисперсия s², являющуюся смещенной оценкой.

Для проверки того, что полученные оценки максимизируют значение функции правдоподобия, возьмем вторые производные

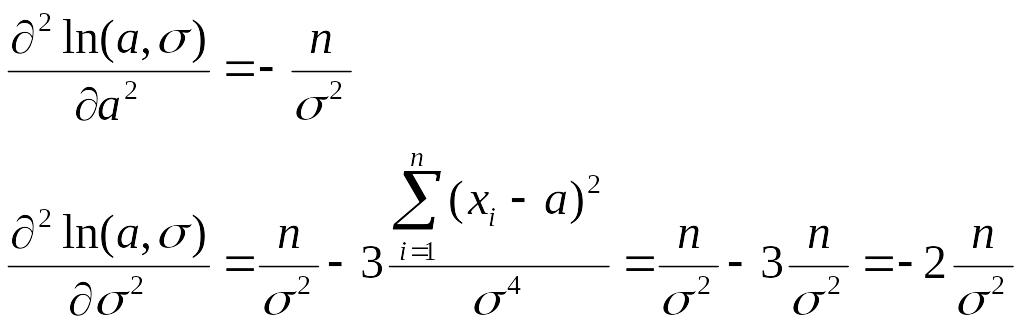
Вторые производные от функции lnL(а, ) независимо от значений параметров меньше нуля, следовательно, найденные значения параметров являются оценками максимального правдоподобия.