9.1. Точечная оценка параметров распределения

Точечная оценка предполагает нахождение единственной числовой величины, которая и принимается за значение параметра. Такую оценку целесообразно определять в тех случаях, когда объем ЭД достаточно велик. При малом объеме ЭД точечные оценки могут значительно отличаться от истинных значений параметров, что делает их непригодными для использования.

9.1.1. Точечная оценка математического ожидания

В качестве приближенного значения (статистической оценки) математического ожидания будем использовать выборочную среднюю .

Будем рассматривать как случайную величину , а х₁, х₂,…, х_п (значения исследуемой случайной величины, составляющие выборку) – как независимые, одинаково распределенные случайные величины Х₁, Х₂,…, Х_п, имеющие математическое ожидание а.

Выясним состоятельность, несмещенность и эффективность выборочной средней как точечной оценки математического ожидания.

Несмещенность

Теорема. Пусть М(Х₁)=…=М(Х_n)=М(Х), тогда средняя арифметическая

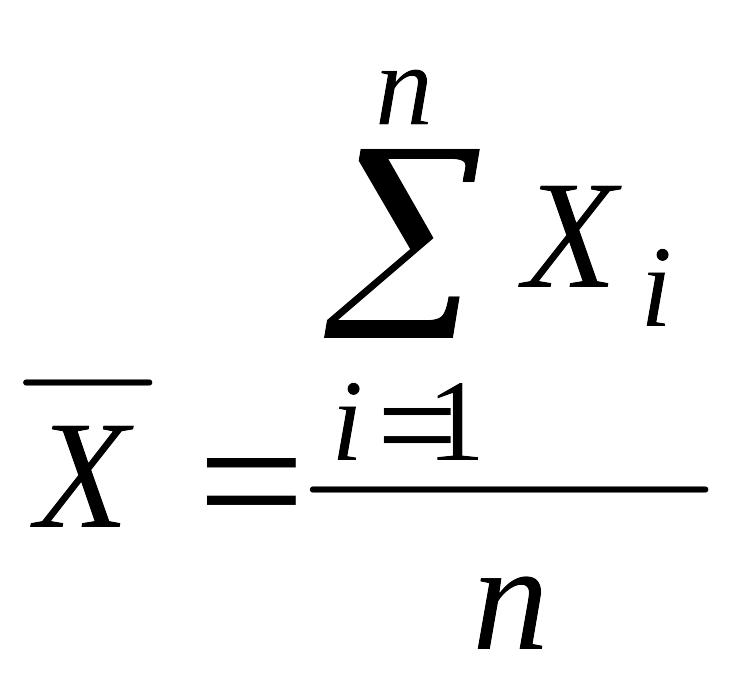
является несмещенной оценкой математического ожидания М(Х).

Доказательство. Если М(Х₁)=…=М(Х_n)=М(Х), то при любом n имеет место следующее свойство математического ожидания

,

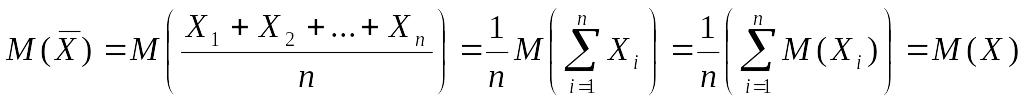то есть .

Таким образом, если , а , то является несмещенной оценкой математического ожидания М(Х).

Выборочное среднее является не только несмещенной, но и состоятельной оценкой математического ожидания.

Состоятельность.

Теорема. Пусть результаты Х₁,…, Х_n наблюдений величины Х независимые случайные величины и М(Х₁)=…=М(Х_n)=М(Х), и дисперсии D(Х₁)=…D(Х_n) конечны. Тогда средняя – состоятельная оценка математического ожидания М(Х).

Если предположить, что Х₁, Х₂,…, Х_п имеют ограниченные дисперсии, то из теоремы Чебышева следует, что их среднее арифметическое, то есть , при увеличении п стремится по вероятности к математическому ожиданию а каждой их величин, то есть к М(Х):

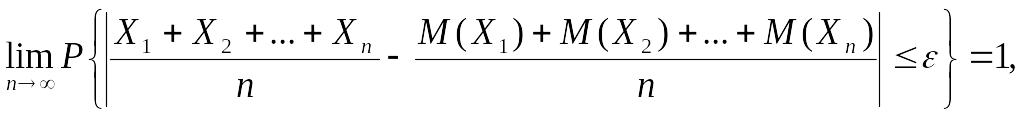
которое, учитывая условие М(Х₁)=…=М(Х_n)=М(Х), можно записать

.

Из определения состоятельности следует, что если , а , то выборочная средняя является состоятельной оценкой математического ожидания.

Эффективность.

Напомним, что свойство эффективности рассматривается только для несмещенных оценок. Докажем эффективность для случая, когда случайная величина Х имеет нормальный закон распределения.

Теорема. Пусть случайная величина Х имеет нормальный закон распределения и при этом результаты Х₁,…, Х_n ее наблюдений независимы, а так же выполняются условия: М(Х₁)=…=М(Х_n)=М(Х) и D(Х₁)=…=D(Х_n)=D(Х). Тогда средняя арифметическая – это несмещенная эффективная оценка математического ожидания М(Х).

Доказательство. Для доказательства эффективности докажем, что ее дисперсия совпадает с минимальной границей, равной в случае нормального распределения .

.

Таким образом, - несмещенная эффективная оценка математического ожидания М(Х).

9.1.2. Точечная оценка дисперсии

Наряду с выборочной дисперсией

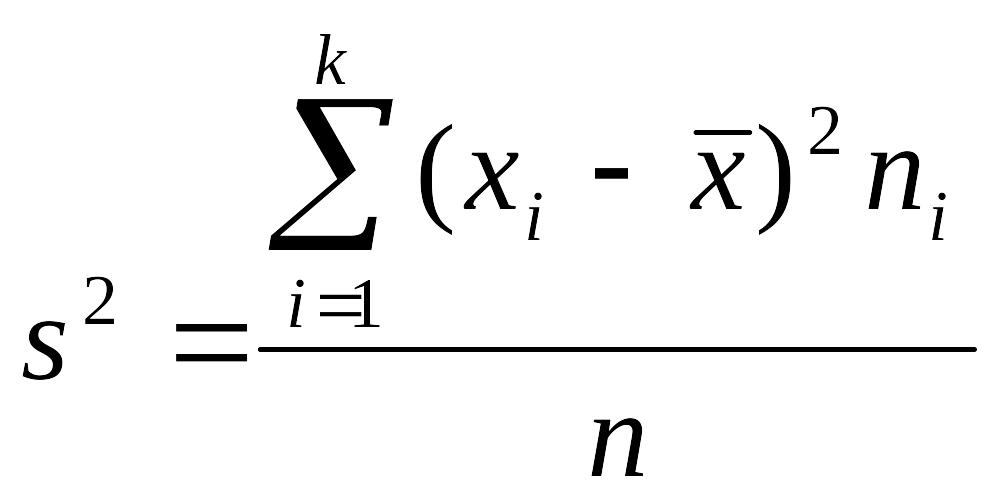
в качестве приближенного значения (возможной оценки) генеральной дисперсии будем использовать величину

,

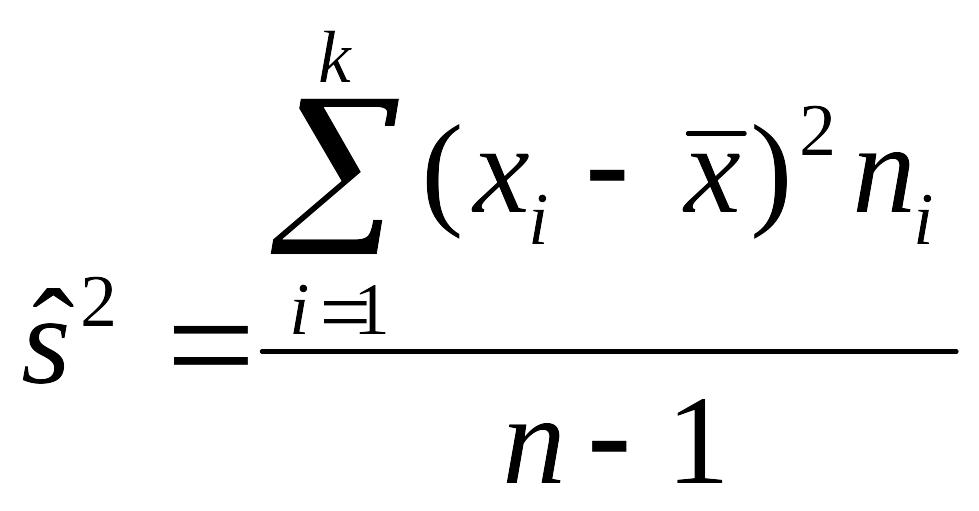которая связана с s² соотношением

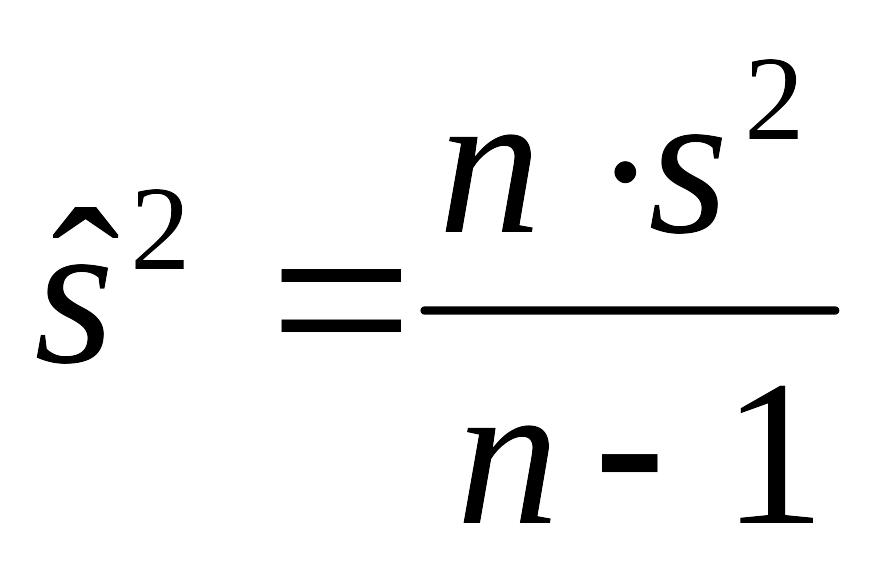
Выясним их состоятельность, несмещенность и эффективность.

Состоятельность.

Теорема. Пусть результаты Х₁,…, Х_n наблюдений величины Х независимые случайные величины и М(Х₁)=…=М(Х_n)=М(Х), а дисперсии D(Х₁)=…D(Х_n)= D(Х) , а центральные моменты второго и третьего порядков величины Х конечны. Тогда при любом ε>0 имеет место равенство :

т.е. s² – состоятельная оценка генеральной дисперсии D(Х) и

,

т.е. – состоятельная оценка генеральной дисперсии D(Х).

Несмещенность.

Покажем, что s² является смещенной оценкой дисперсии D(Х), так как при n=2 М(s²)≠ D(Х).

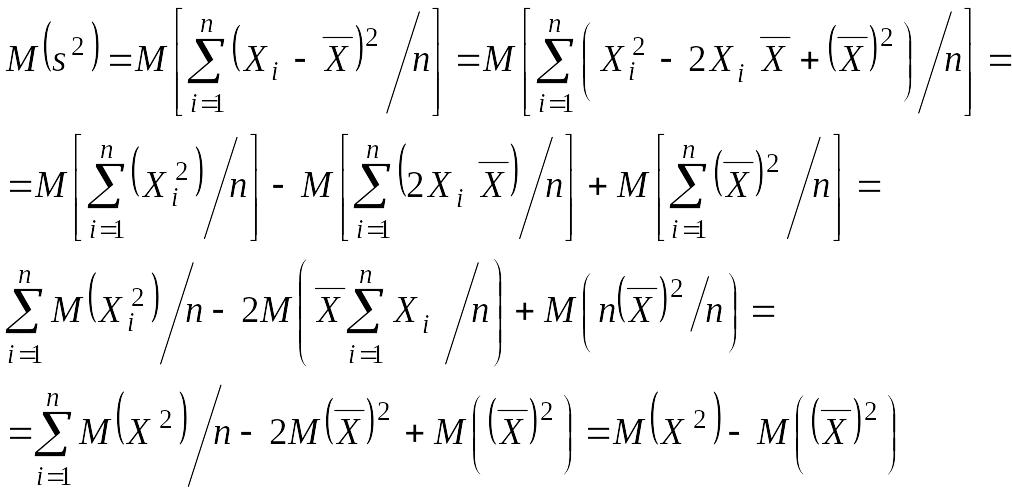
но

.

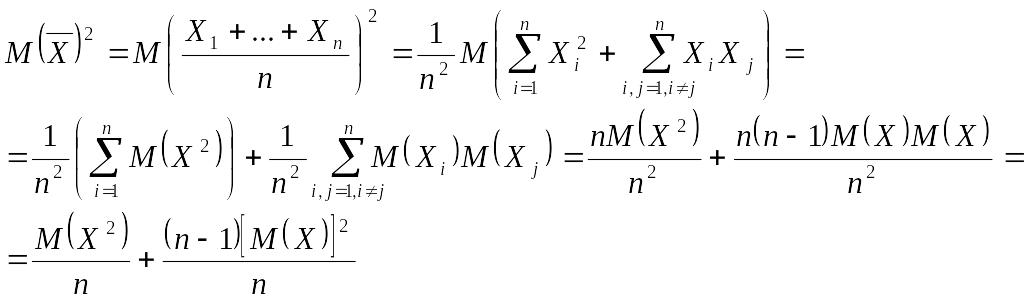
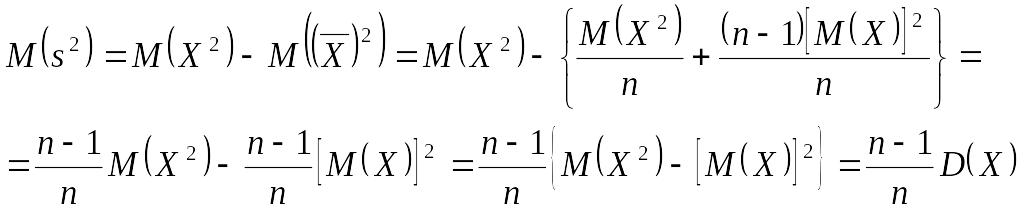Таким образом, – s² является смещенной оценкой дисперсии D(Х) и смещение равно .

Теорема. Пусть результаты Х₁,…, Х_n наблюдений величины Х независимы, а М(Х₁)=…=М(Х_n)=М(Х) и дисперсии D(Х₁)=…D(Х_n)= D(Х). Тогда – несмещенная оценка дисперсии D(Х).

Доказательство. Найдем :

.

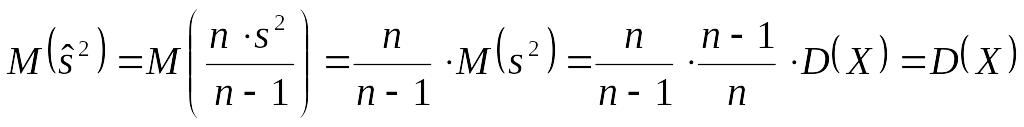Итак при любом n , т.е. если , а , то является несмещенной оценкой дисперсии D(Х).

Эффективность.

Пусть случайная величина Х имеет нормальный закон распределения. Для доказательства эффективности докажем, что ее дисперсия совпадает с минимальной границей, равной в случае нормального распределения .

Предположим, что результаты Х₁,…, Х_n наблюдений случайной величины Х независимы и имеют тот же закон распределения, что и случайная величина Х. При выполнении этих условий выполняется соотношение: . Поэтому

.

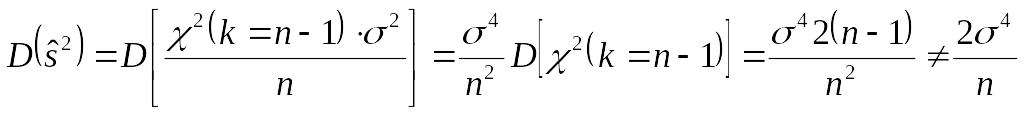Так как не совпадает с нижней границей, то будучи несмещенной оценкой дисперсии D(Х), не является эффективной оценкой.