8.4. Начальные центральные моменты

Средняя арифметическая и дисперсия статистического ряда являются частными случаями более общих понятий – моментов статистического ряда.

Начальный момент k–го порядка статистического ряда определяется по формуле:

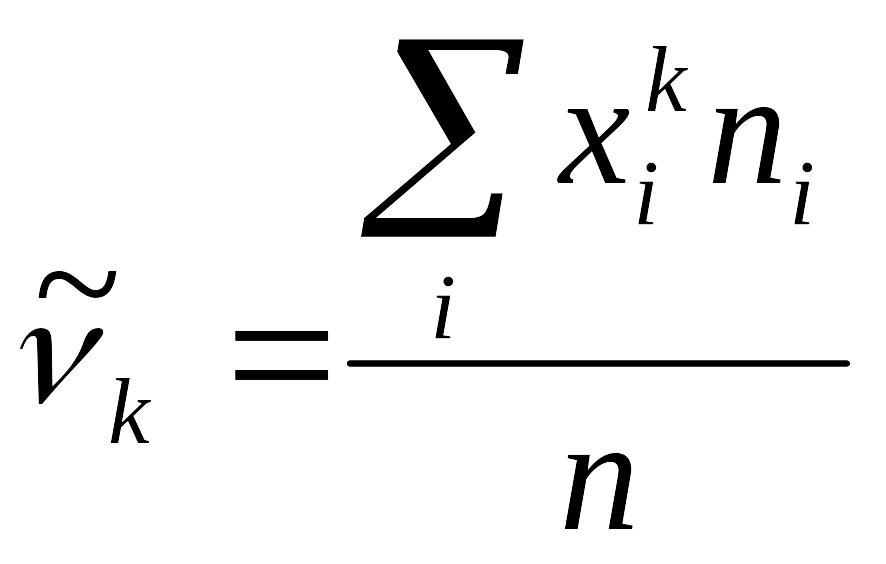или

Очевидно, что средняя арифметическая является моментом первого порядка статистического ряда: .

Центральный момент порядка s статистического ряда определяется по формуле:

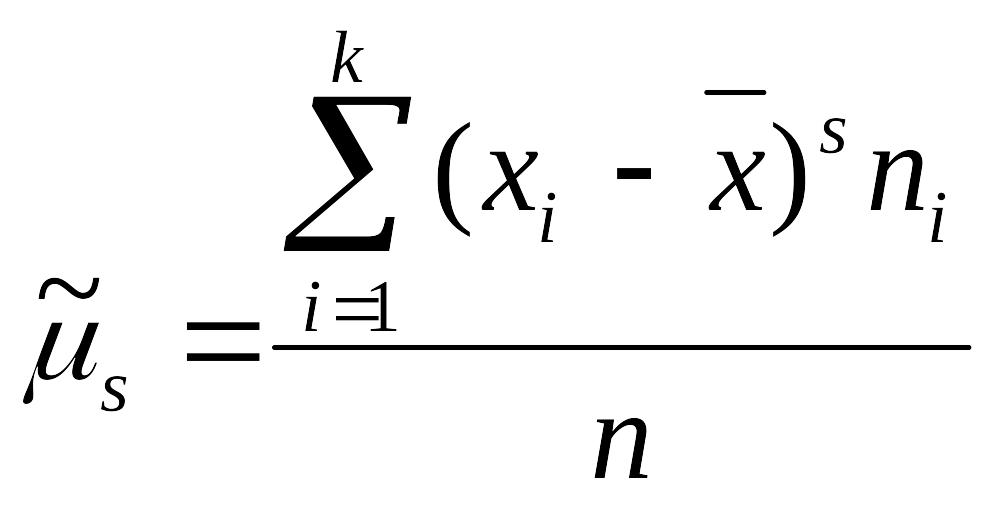или

Нетрудно заметить, что при при s=1 первый центральный момент равен нулю, а при s=2 второй центральный момент - это выборочная дисперсия статистического ряда, т.е. .

Центральные моменты удобно рассчитывать по начальным моментам по формулам:

.

Форма распределения выборочной совокупности характеризуется коэффициентом ассиметрии и эксцесса.

Коэффициентом асимметрии статистического ряда называется число:

.

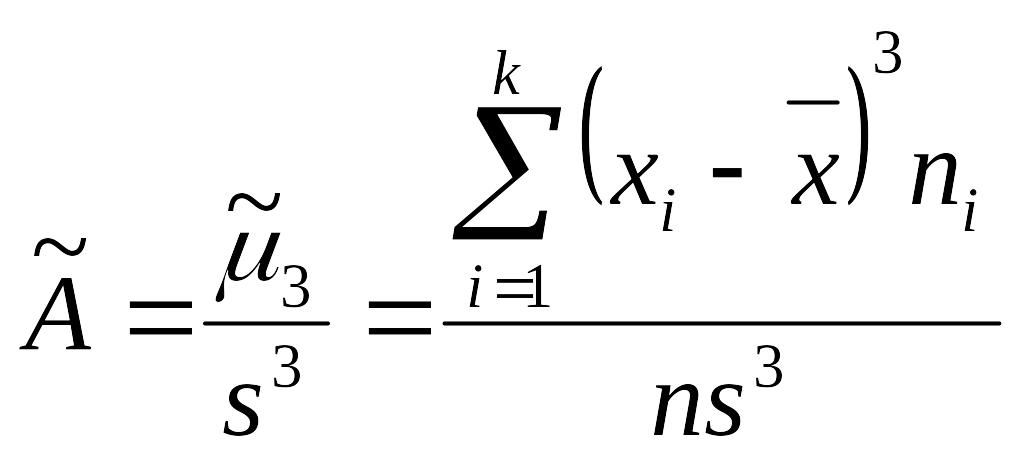Если , то распределение имеет симметричную форму, т.е. варианты равноудалены от и имеют одинаковую частоту. Если асимметрия – положительная, то распределение сдвигается влево, если отрицательная – вправо.

Эксцесс вариационного ряда называется число:

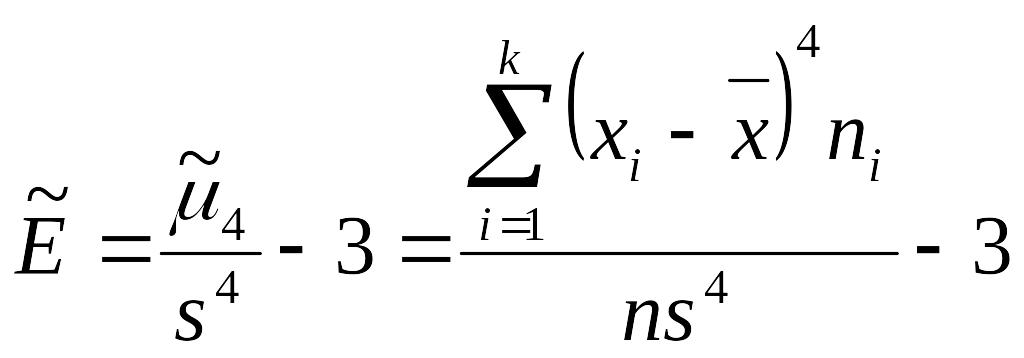
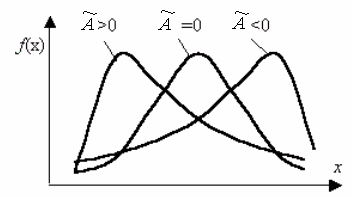
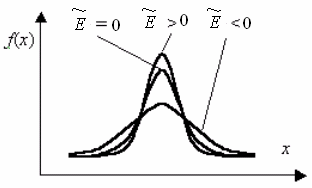
Эксцесс – это мера крутости кривой распределения. Кривая распределения может быть островершинной, плосковершинной, средне вершинной. Если , то распределение имеет нормальную форму. Если эксцесс– положительный, то полигон имеет более крутую вершину по сравнению с нормальной кривой, если отрицательный – более пологую.

Эти четыре момента составляют набор особенностей распределения при анализе данных.

Глава 9. Оценки параметров распределения и их свойства

Одна из задач математической статистики: по имеющейся выборке оценить значения числовых характеристик исследуемой случайной величины.

Здесь речь идет об оценках (приближенных значениях) основных параметров распределения случайных величин: математического ожидания , дисперсии , среднего квадратического отклонения случайной величины X, ковариации и коэффициента корреляции между двумя любыми случайными величинами X и Y, а также вероятности наступления случайного события p. Для удобства обозначим любой из перечисленных параметров символом (тета).

Статистической оценкой неизвестного параметра распределения называется любая функция от значений выборки , т.е. статистика.

Пусть распределение случайной величины (генеральной совокупности) задается вероятностями (для дискретной случайной величины) или плотностью вероятности (для непрерывной случайной величины), которые зависят от неизвестного параметра . Этим параметром может быть, например, параметр закона Пуассона или параметры а и нормального распределения. На практике о величине параметра можно судить по выборке объема n из генеральной совокупности.

Пусть по выборке объема найдена оценка . При повторении опыта происходит извлечение другой выборки того же объема из генеральной совокупности, и получается другая оценка неизвестного теоретического параметра . Повторяя опыт далее раз, получаем (в общем случае) различных чисел , ,…, . Поэтому оценку можно рассматривать как случайную величину, которая может принимать значения , ,…, .

Задача состоит в том, чтобы найти такую оценку , которая была бы в определенном смысле наиболее близкой к оцениваемому параметру θ.

Для того чтобы оценка давала «хорошие» приближения она должна быть: несмещенной, эффективной, состоятельной.

Несмещенной оценкой параметра θ называется статистическая оценка , если ее математическое ожидание совпадает со значением оцениваемого теоретического параметра при любом объеме выборки:

.

Смещенной оценкой называется оценка , математическое ожидание которой не равно значению теоретического параметра.

Таким образом, если , то мы будем получать при вычислении оценок систематические ошибки.

Асимптотически несмещенной оценкой называется статистическая оценка , если её математическое ожидание совпадает со значением оцениваемого теоретического параметра:

при .

Смещением оценки называется величина .

Свойство несмещенности является свойством оценок при фиксированном . Такая оценка не всегда дает хорошее приближение теоретического параметра, так как ее возможные значения могут быть значительно рассеяны относительно своего среднего значения. Это означает большую дисперсию , поэтому если в качестве оцениваемого параметра взять его несмещенную оценку, то распределение было бы установлено ошибочно. С минимизацией дисперсии оценки связано требование ее эффективности.

Состоятельной оценкой параметра θ называется статистическая оценка, которая при сходится по вероятности к истинному значению параметра, т.е.

,

Это необходимое свойство оценки, несостоятельными оценками пользоваться не рекомендуется.

Эффективной оценкой называется несмещенная статистическая оценка , если среди всех подобных оценок той же характеристики она имеет наименьшую дисперсию:

.

Так для случайной величиной Х, имеющей нормальный закон распределения с дисперсией σ²,

• нижняя граница для дисперсий различных несмещенных оценок математического ожидания равна ,

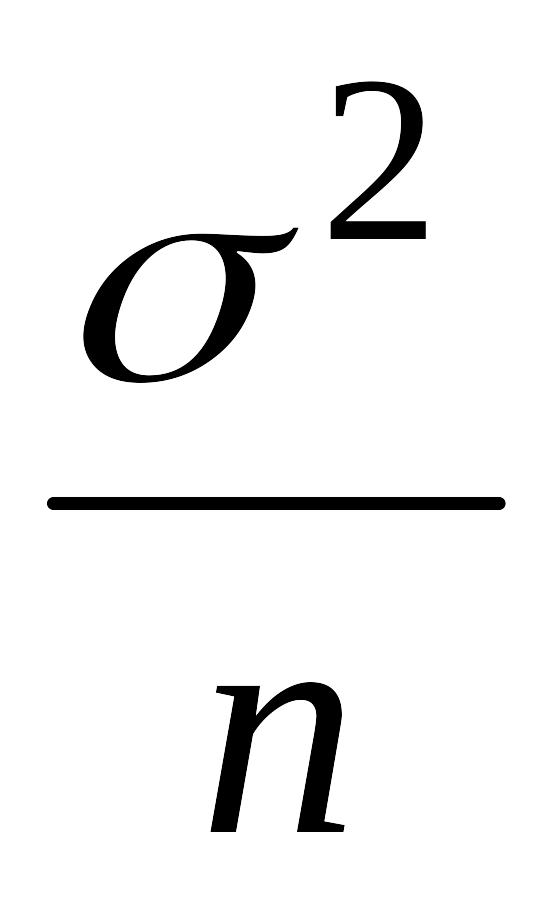• нижняя граница для дисперсий различных несмещенных оценок дисперсии равна .

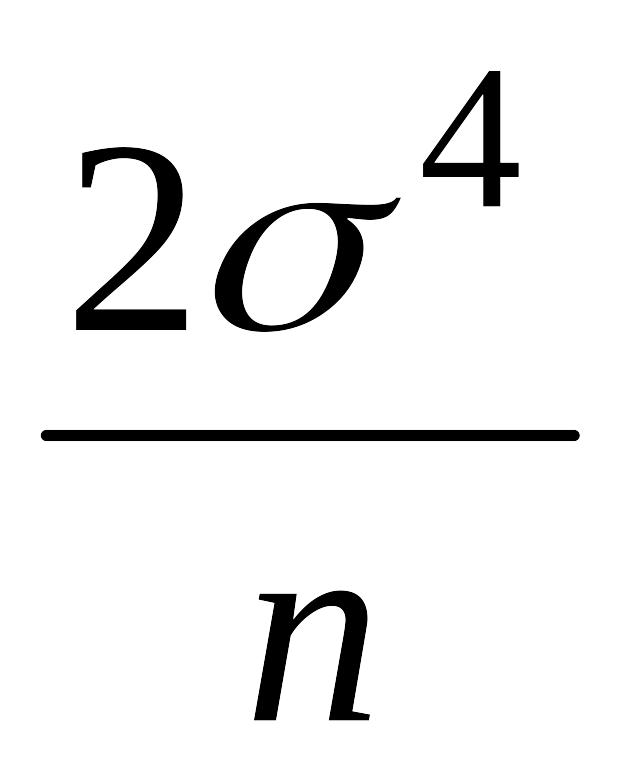Для случайной величиной Х, выражающеей число наступлений события А в одном испытании,и имеющей закон распределения

xi	0	1
рi	q	р

• нижняя граница для дисперсий различных несмещенных оценок вероятности р равна .

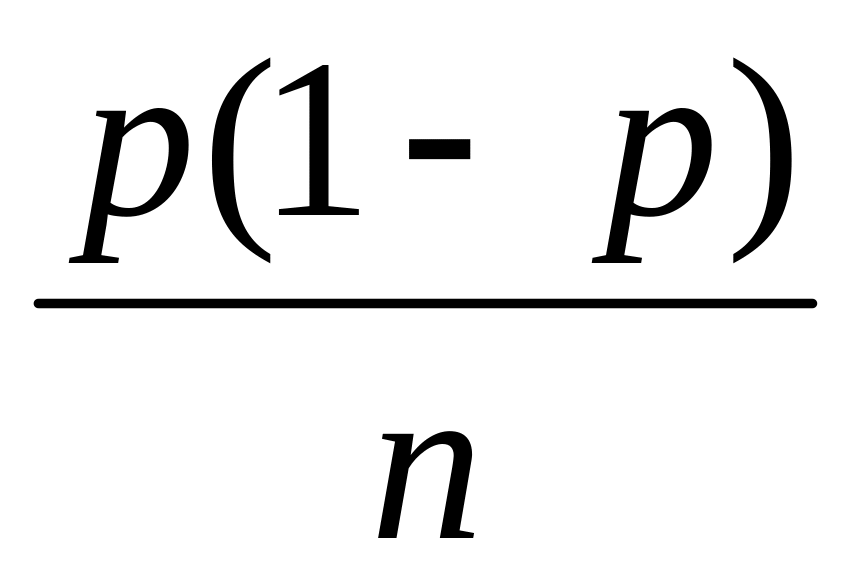Различают два вида оценок – точечные и интервальные.

Точечными называют такие оценки, которые характеризуются одним числом.

Интервальные оценки задаются двумя числами, определяющими вероятный диапазон возможного значения параметра.