
- •Глава 8. Числовые характеристики выборки
- •8.1. Средние величины как характеристики положения
- •8.2. Показатели вариации как характеристики рассеяния
- •Свойства дисперсии:
- •8.3. Упрощенный способ расчета средней арифметической и дисперсии
- •8.4. Начальные центральные моменты
- •Глава 9. Оценки параметров распределения и их свойства
- •9.1. Точечная оценка параметров распределения
- •9.1.1. Точечная оценка математического ожидания
- •9.1.2. Точечная оценка дисперсии
- •9.1.3. Частость как точечная оценка вероятности события
- •9.2. Методы оценки параметров распределения
- •9.2.1. Метод максимального правдоподобия (ммп)
- •9.2.2. Метод моментов
- •9.2.3. Метод наименьших квадратов (мнк)
- •9.3. Интервальная оценка параметров распределения
- •9.4. Построение доверительных интервалов
- •9.4.1. Доверительный интервал для оценки математического ожидания нормального распределения при известной дисперсии
- •9.4.2. Доверительный интервал для оценки математического ожидания нормального распределения при неизвестной дисперсии
- •9.4.3. Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения
- •9.4.4. Доверительный интервал для вероятности
8.2. Показатели вариации как характеристики рассеяния
Средние величины не отражают изменчивости значений признака. Для оценки меры неоднородности (разброса, изменчивости) выборки наряду со средними значениями вычисляют и характеристики рассеяния.
Вариацией какого-либо параметра (показателя) в совокупности наблюдений называется различие его значений у разных элементов этой совокупности. Именно это свойство является объектом исследования большинства методов обработки ЭД.
Вариационный размах – это разность максимального и минимального значений статистического ряда: R= xmax –xmin.
Наибольший интерес представляют меры вариации (рассеяния) наблюдений вокруг средних величин.
Средним
линейным отклонением
статистического ряда называется средняя
арифметическая
абсолютных величин отклонений вариантов
от их средней:
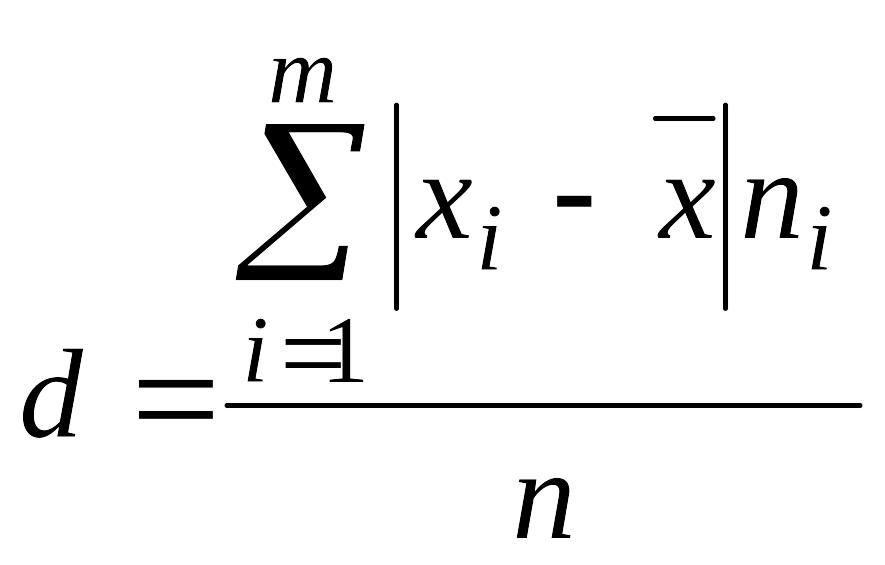
Выборочной дисперсией s2 статистического ряда называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической:
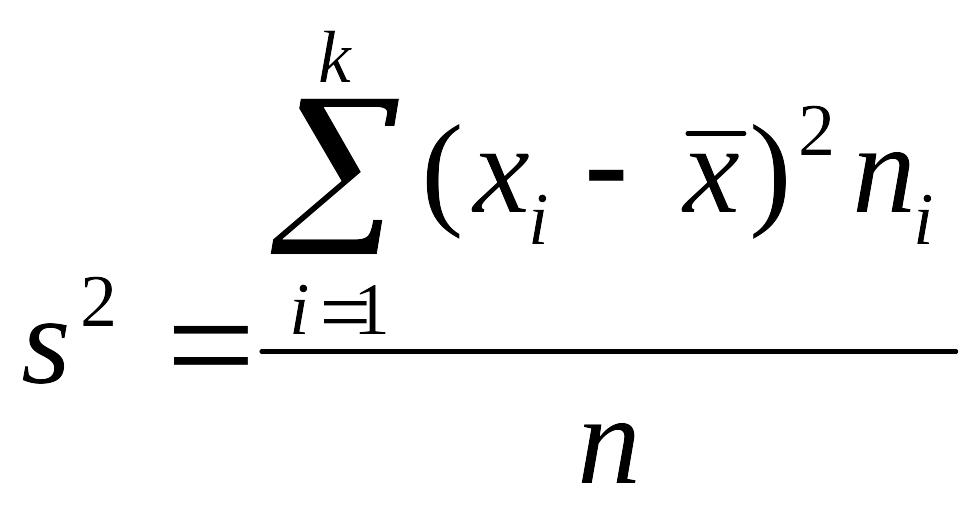 или
или
![]() .
.
Для
несгруппированного
ряда (ni=1):
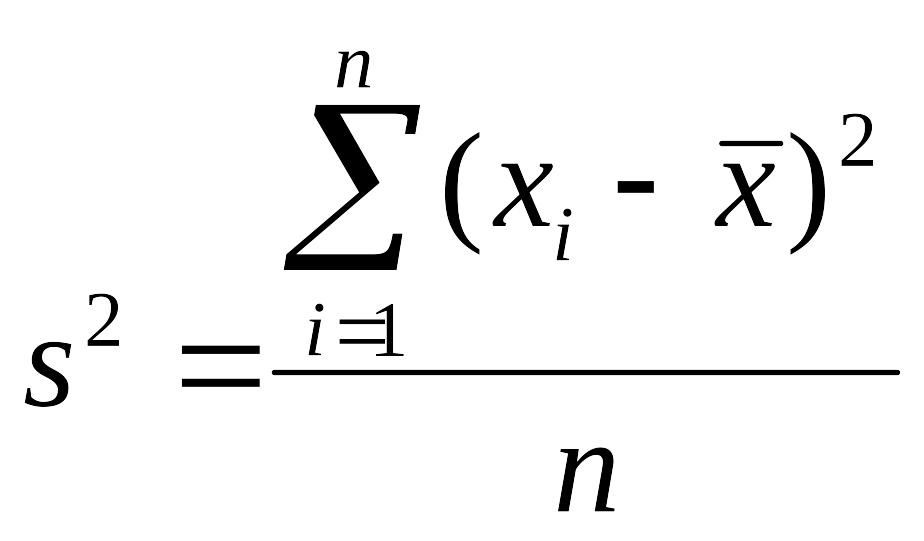 .
.
Среднее квадратическое отклонение (стандартным отклонением) s статистического ряда – арифметическое значение корня квадратного из выборочной дисперсии:
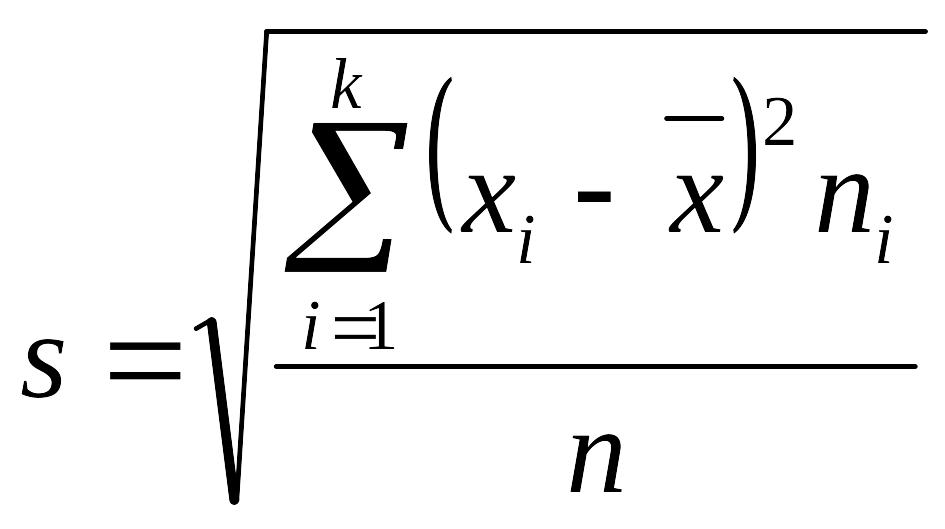 или
или
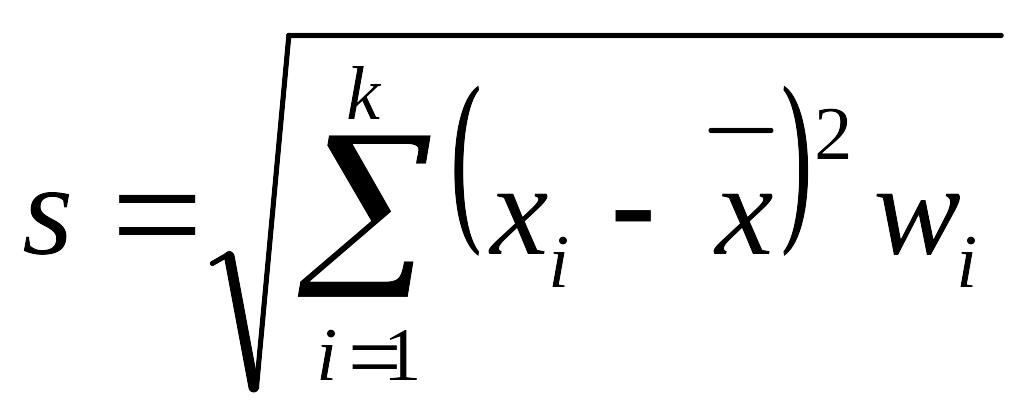 .
.
Размерность стандартного отклонения в отличие от размерности дисперсии совпадает с единицами измерения варьирующего признака, поэтому в практической статистике для того, чтобы охарактеризовать рассеяние признака используют обычно стандартное отклонение, а не дисперсию.
Свойства дисперсии:
Дисперсия постоянной равна нулю:
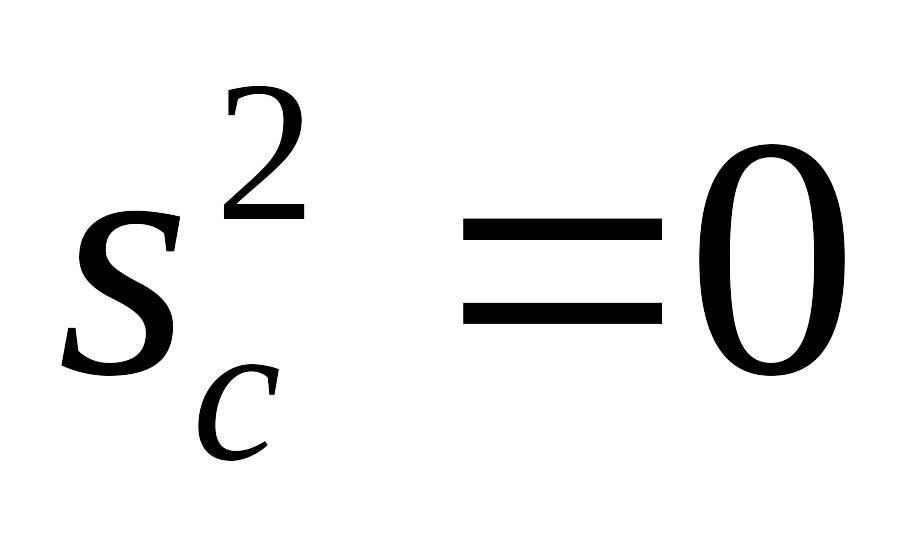 .
.Если все варианты увеличить (уменьшить) на одну и туже постоянную, то дисперсия не изменится:
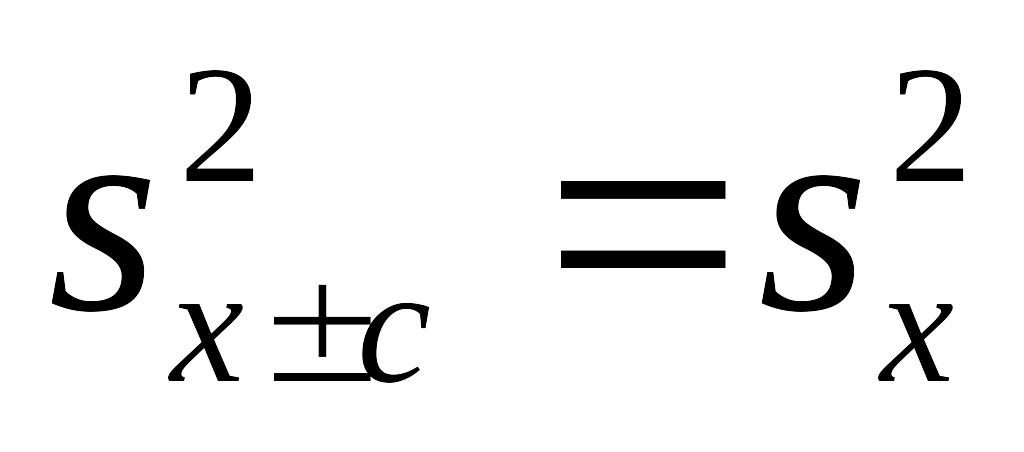 .
.Если все варианты увеличить (уменьшить) в одно и то же число k раз, то дисперсия увеличивается (уменьшится) в k2 раз:
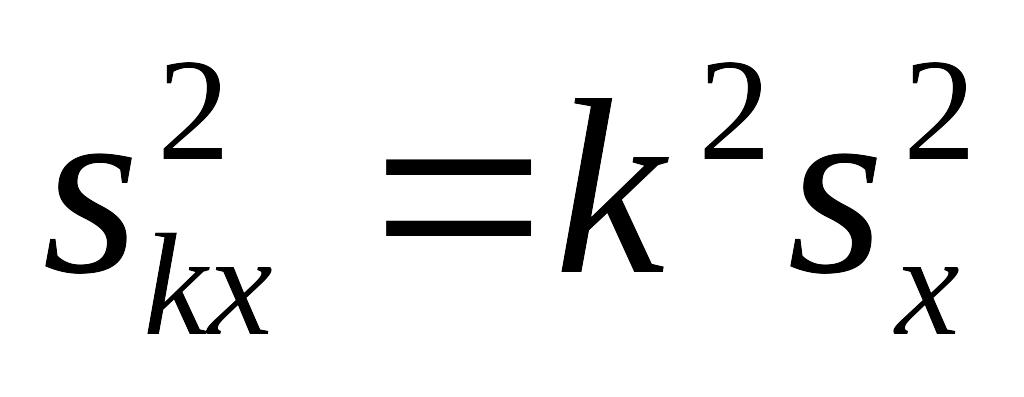 .
.Дисперсия равна разности между средней арифметической квадратов вариантов и квадратом средней арифметической:
 .
.Если ряд наблюдений состоит из нескольких групп, общая дисперсия равна сумме средней арифметической групповых дисперсий (внутригрупповая дисперсия) и межгрупповой дисперсии («правило сложения дисперсий»):
![]() ,
,
где
![]() – общая дисперсия (дисперсия всего
ряда);
– общая дисперсия (дисперсия всего
ряда);
![]() – средняя
арифметическая групповых дисперсий
– средняя
арифметическая групповых дисперсий
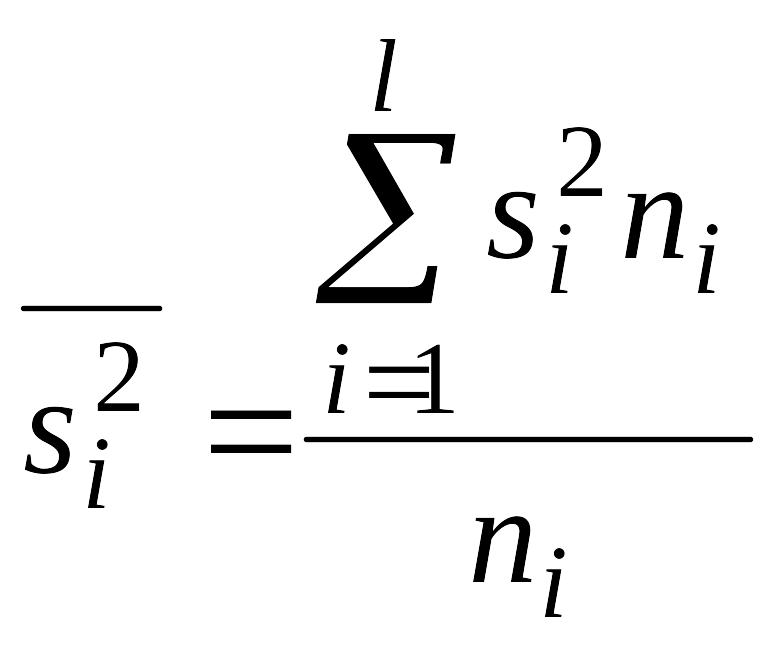 (внутригрупповая
дисперсия);
(внутригрупповая
дисперсия);
![]() –
дисперсия
i
–ой
группы
–
дисперсия
i
–ой
группы
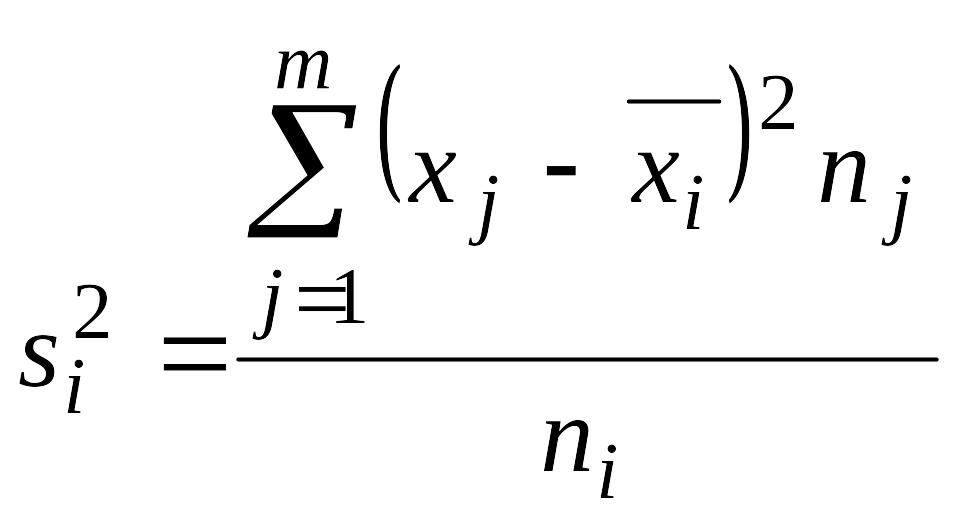 ,
объем которой равен ni,
,
объем которой равен ni,
![]() - групповая
средняя;
- групповая
средняя;
![]() –
межгрупповая
дисперсия
–
межгрупповая
дисперсия
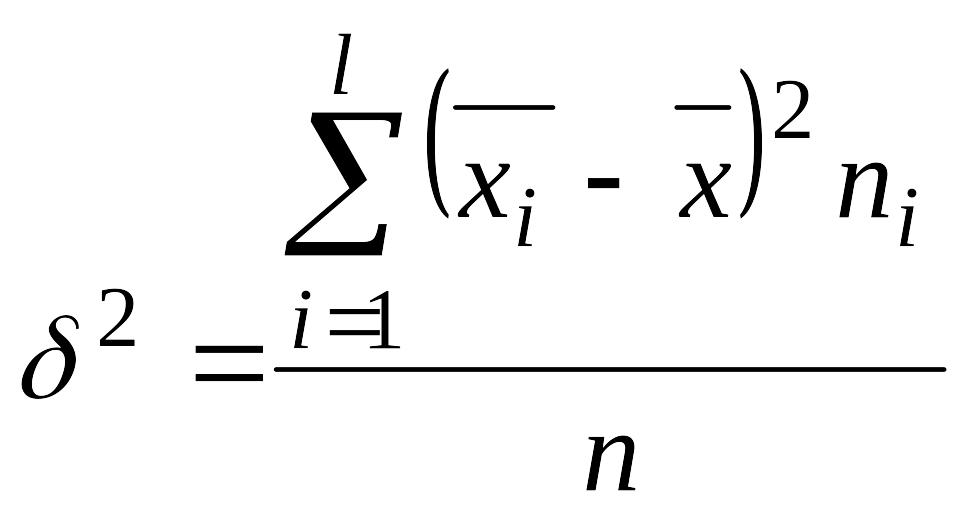 ,
где
,
где
![]() - общая
средняя;
- общая
средняя;
l- число групп.
Если требуется сопоставить стандартные отклонения со средними арифметическими этих признаков, то вводится относительный показатель, называемый коэффициентом вариации.
Коэффициент вариации – это процентное отношение среднего квадратического отклонения к средней арифметической:
![]()
Коэффициент вариации является относительной мерой рассеяния признака.
Коэффициент вариации используется и как показатель однородности выборочных наблюдений. Считается, что если коэффициент вариации не превышает 10%, то выборку можно считать однородной, т.е. полученной из одной генеральной совокупности.
8.3. Упрощенный способ расчета средней арифметической и дисперсии
Условными называют варианты, определяемые равенством
![]() ,
,
где с и h – специально подобранные числа:
с –ложный нуль (новое начало отсчета; чаще всего это середина серединного интервала, если серединных интервалов два, то за с берут середину одного из этих интервалов),
h – шаг, т.е разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба).
Упрощенный метод расчета характеристик выборки основан на замене первоначальных вариант на условные. Согласно свойствам средней арифметической и дисперсии
![]()
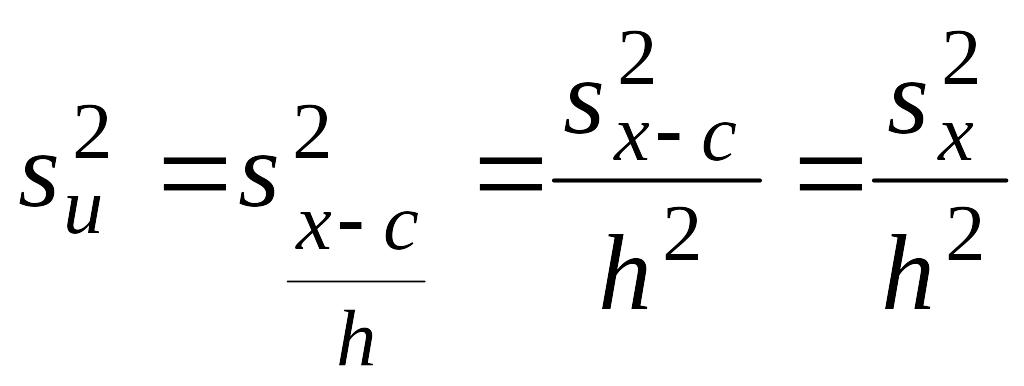
откуда
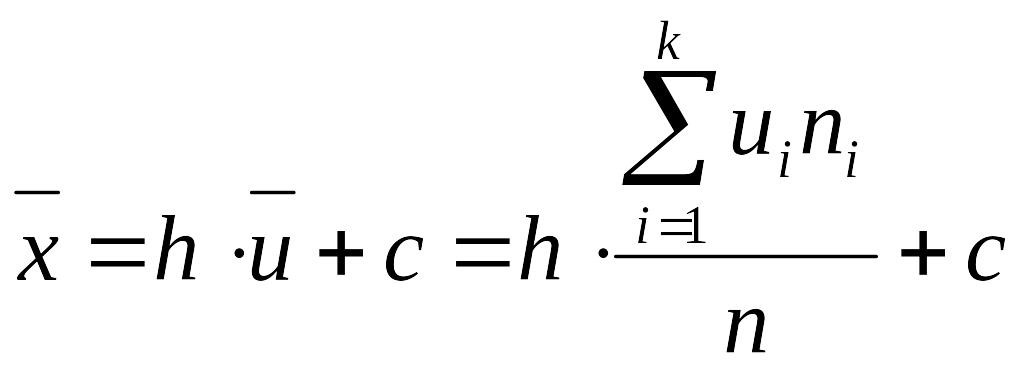
![]()
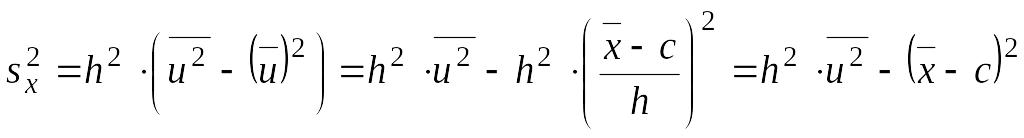
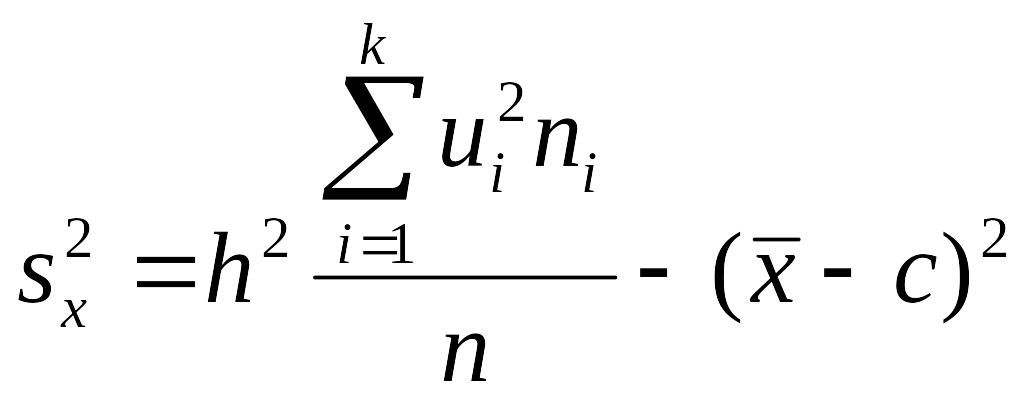 .
.
