Глава 8. Числовые характеристики выборки

Построив вариационный ряд и изобразив его графически, можно получить первоначальное наглядное представление о ряде наблюдений. Однако обилие числовых данных усложняет их использование. В то же время на практике часто оказывается достаточным знание лишь сводных характеристик вариационных рядов: средних или характеристик центральной тенденции; характеристик изменчивости (вариации).

Вариационные ряды и графики эмпирических распределений дают наглядное представление о том, как варьирует признак в выборочной совокупности. Но они недостаточны для полной характеристики выборки, поскольку содержат много деталей, охватить которые невозможно без обобщающих числовых характеристик.

Числовые характеристики выборки дают количественное представление об эмпирических данных и позволяют сравнивать их между собой. Наибольшее практическое значение имеют характеристики положения, рассеяния и асимметрии эмпирических распределений.

Поскольку эти величины получаются по выборочным данным, их обычно называют статистическими характеристиками или оценками.

8.1. Средние величины как характеристики положения

Средние величины характеризуют значение признака, вокруг которого концентрируются наблюдения. Наиболее распространенной из средних величин является средняя арифметическая.

Главное назначение средних величин состоит в их обобщающей функции. Это обобщение позволяет заменить множество различных индивидуальных значений показателя средней величиной, характеризующей всю однородную совокупность. Иначе говоря, средняя величина является типической характеристикой варианты в конкретной выборке. Иногда средняя величина обобщает и неоднородные показатели однотипных объектов.

Средней арифметической невзвешенной (простой) или выборочной средней статистического ряда называется среднее арифметическое значение элементов выборки:

Такая выборочная средняя используется для несгруппированного ряда (n_i=1).

Если данные представлены в виде статистического ряда, тогда выборочная средняя статистического ряда (средняя взвешенная) определяется по формуле:

,

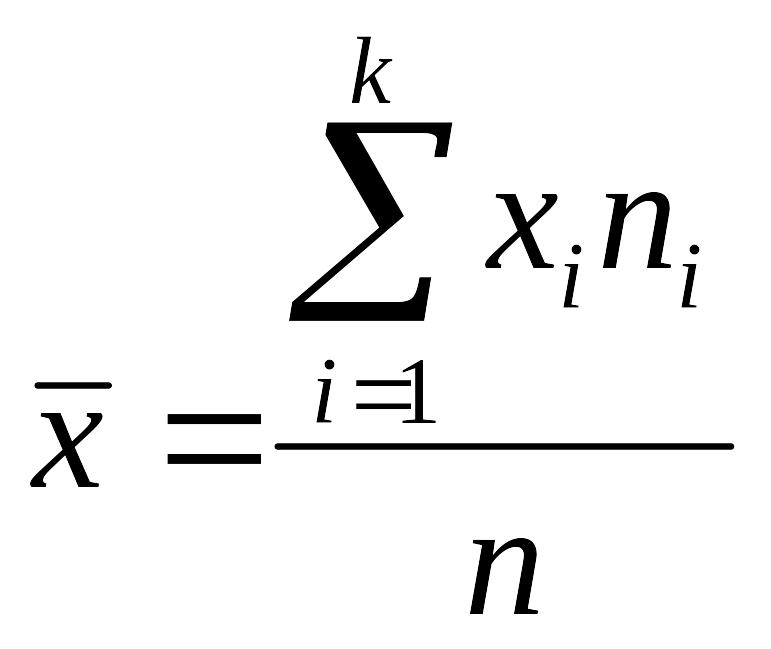где х_i – варианты дискретного или середины интервалов интервального вариационного ряда; n_i – соответствующие им частоты.

Очевидно, что , где – относительные частоты (частости) вариантов или интервалов.

Пример. Рассчитаем средний стаж работы по данным таблицы.

Стаж работы рабочих завода

Табельный номер рабочего	1	2	3	4	5	6	7
Стаж работы (лет)	10	3	5	12	11	7	9

Решение.

С учетом имеющихся данных получим:

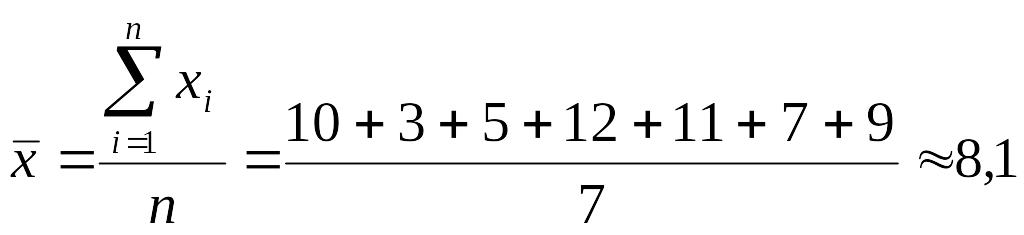года.

Пример. Найдем средние продажи колбасы в месяц по данным таблицы.

i	выработка в отчет. году в % к предыдущему х	Середина интервала	частота ni
	4,25–5,95	3	4	20,4
	5,95–7,65	10	7	47,6
	7,65–9,35	21	16	136
	9,35–11,05	41	9	91,8
	11,05–12,72	69	6	71,4
	12,75–14,45	88	5	68
	14,45–16,15	98	3	45,9
Σ		50	–	481,1

Решение.

С учетом имеющихся данных получим:

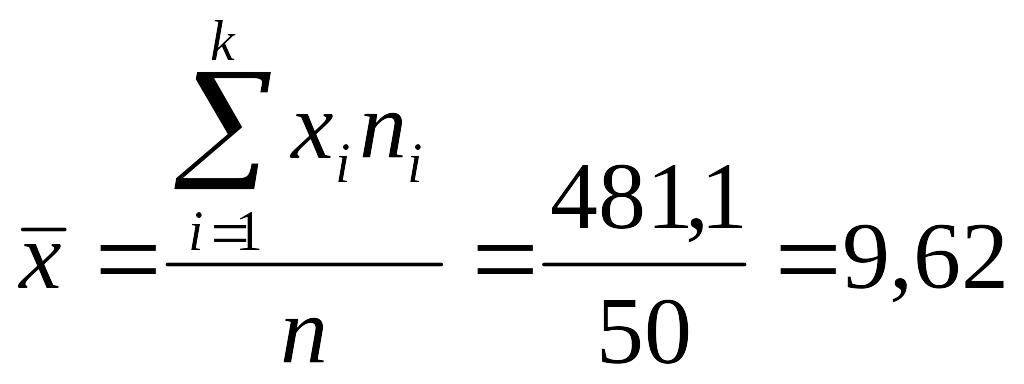млн. руб.

Нахождение среднего арифметического интервального ряда осложняется если крайние интервалы не замкнуты (то есть имеют вид «менее 10» или «более 60»). В этом случае считается, что ширина первого интервала равна ширине второго, а ширина последнего – ширине предпоследнего.

Отметим, что средняя арифметическая – величина той же размерности, что и значения случайной величины.

Свойства средней арифметической

1. Средняя арифметическая постоянной равна самой постоянной: .

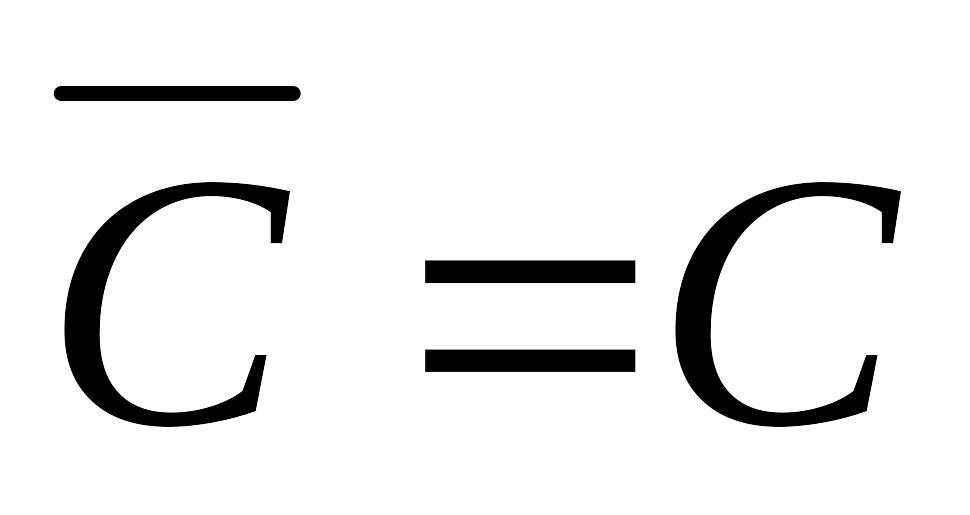2. Если все варианты увеличить (уменьшить) на одну и туже постоянную, то средняя арифметическая увеличивается (уменьшится) на то же число: .

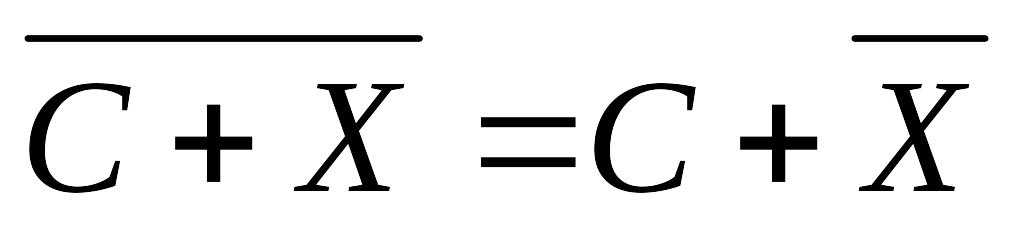3. Если все варианты увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличивается (уменьшится) во столько же раз: .

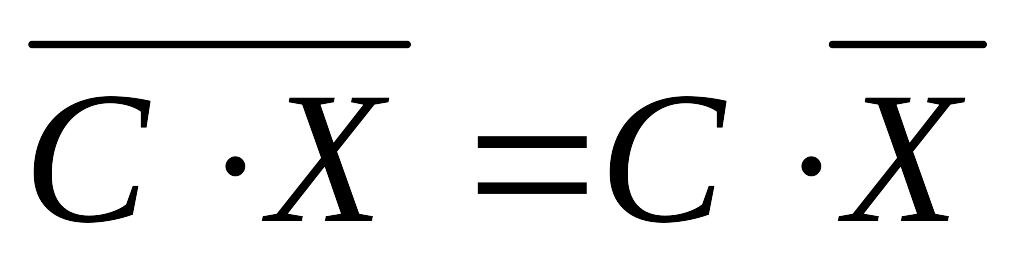4. Сумма отклонений вариантов от их средней арифметической равно нулю:

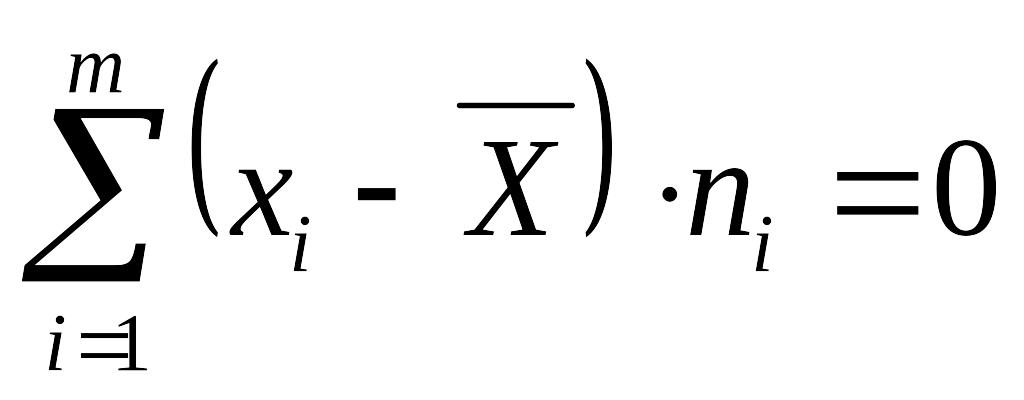
5. Средняя арифметическая алгебраической суммы нескольких признаков равна такой же сумме средних арифметических этих признаков:

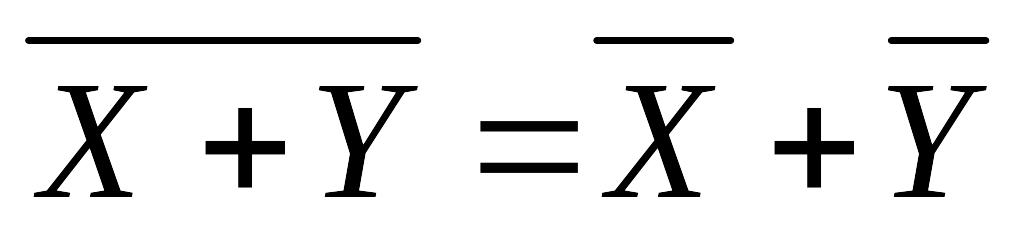
6. Если ряд наблюдений состоит из нескольких групп, общая средняя равна средней арифметической групповых средних, причем весами являются объемы групп: ,

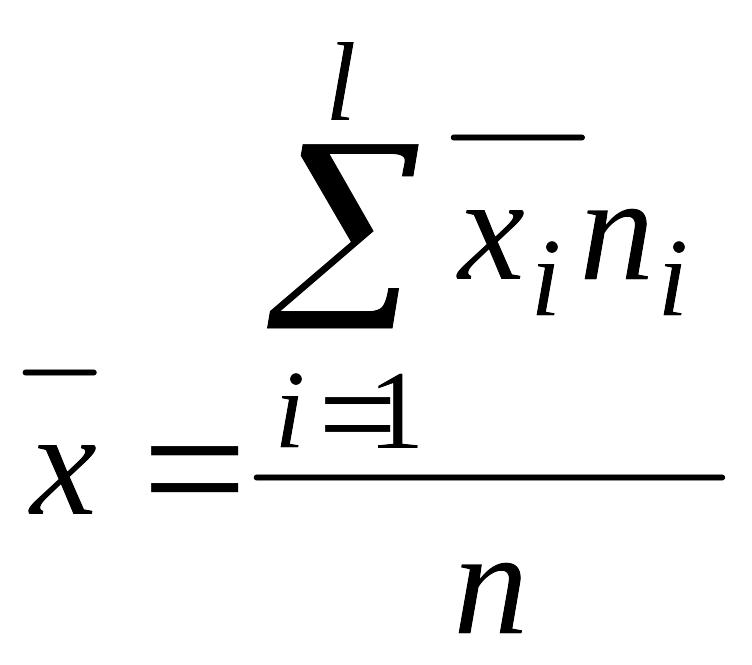где – общая средняя (средняя арифметическая всего ряда);

– групповая средняя i –ой группы, объем которой равен n_i;

l – число групп.

Рассмотренные средние величины называются аналитическими. В статистическом анализе применяют так же и структурные или порядковые средние. К ним относятся мода и медиана.

Модой статистического ряда называется вариант, которому соответствует наибольшая частота.

Сложность в том, что редкая совокупность имеет единственную моду. (Например: 2, 6, 6, 8, 9, 9, 9, 10 – мода = 9).

Если два несмежных значения имеют равную и наибольшую в данной группе частоту, то у этого вариационного ряда есть две моды, такая группа называется бимодальной.

Особенность моды заключается в том, что она не меняется при изменении крайних членов ряда, т.е. обладает определенной устойчивостью к вариации ряда. Для интервального ряда :

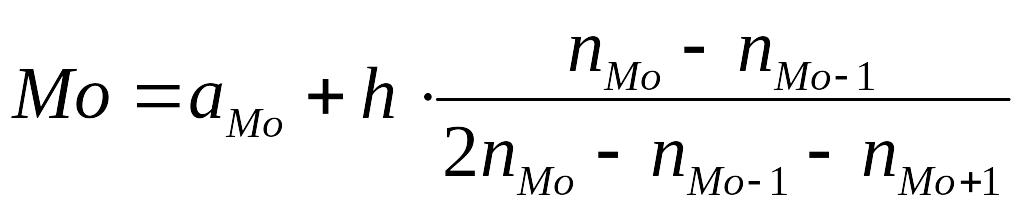, где

– нижняя граница модального интервала;

– ширина интервала группировки;

– частота модального интервала;

– частота интервала, предшествующего модальному;

– частота интервала, следующего за модальным.

Медиана статистического ряда – это значение признака, приходящееся на середину ранжированного ряда наблюдений.

Для дискретного ряда с нечетным числом членов (n=2k+1) медиана равна серединному варианту Mе=x_k+1, а для ряда с четным числом членов (n =2k) – полусумме двух серединных вариантов:

.

Для интервального ряда:

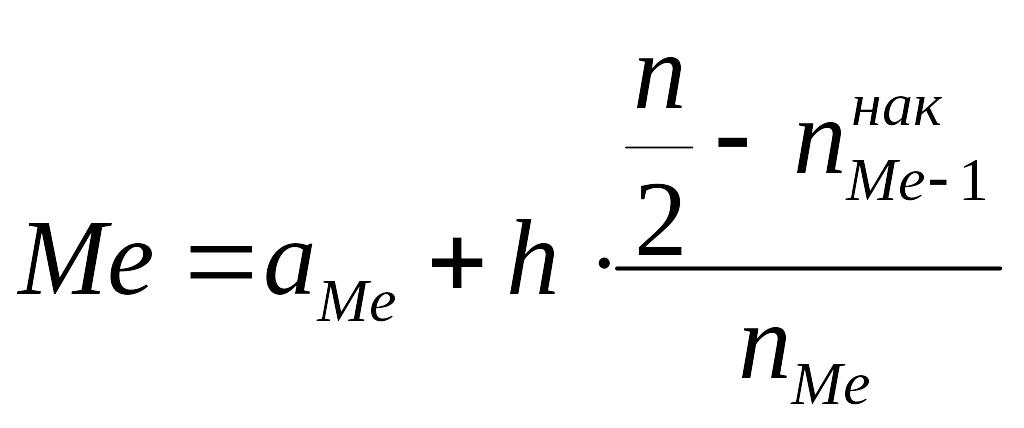, где

– нижняя граница медианного интервала, к которому принадлежит медиана;

– половина объема выборки;

h – ширина медианного интервала;

–частота медианного интервала;

– накопленная частота интервала, предшествующего медианному.

Достоинство медианы заключается в том, что на нее не влияет изменение крайних членов вариационного ряда, если любой из них, меньший медианы, остается меньше нее, а любой, больший медианы, продолжает быть больше нее. Медиана предпочтительнее средней арифметической для ряда, у которого крайние варианты по сравнению с остальными оказались чрезмерно большими или малыми.

Мода наиболее просто вычисляется и при большом количестве измерений достаточно стабильна и близка к медиане и среднему. Медиана вычисляется по сложнее, особенно легко при ранжированных данных. При больших выборках предлагается сначала сгруппировать их, а потом вычислять медиану. Для определения моды и медианы не требуется знание всех остальных значений.

Пример. Найти моду и медиану интервального ряда.

Возрастные группы	Число студентов
До 20 лет	346	346
20 — 25	872	1218
25 — 30	1054	2272
30 — 35	781	3053
35 — 40	212	3265
40 — 45	121	3386
45 лет и более	76	3462
Итого	3462

Решение:

В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на этот интервал приходится наибольшая частота (1054).

Рассчитаем величину моды:

.

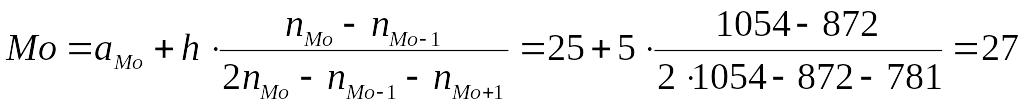Это значит что модальный возраст студентов равен 27 годам.

Вычислим медиану. Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части (n/2 = 3462/2 = 1731). Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:

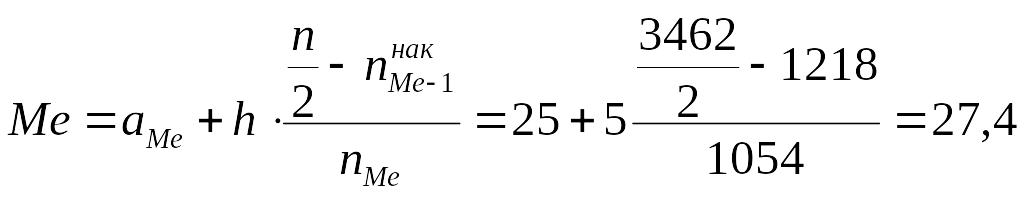
Это значит что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.