3.4 Неподвижная точка и неподвижная прямая аффинного

преобразования плоскости в себя

В первую очередь рассмотрим вопрос о существовании таких точек при аффинном преобразовании плоскости в себя (3.2), при котором эти точки переходили бы в себя, т.е. не меняли бы своего положения на плоскости. Такие точки называются неподвижными или двойными или инвариантными.

Естественно полагать, что для неподвижной точки должно соблюдаться условие: , .

Тогда, в выражение (3.2), запишем как

(3.8)

Решая систему уравнений (3.8) относительно переменных и , можно найти искомые координаты неподвижной точки:

, (3.9)

. (3.10)

Однако, при решение системы уравнений (3.8) при конкретных значениях коэффициентов, могут иметь место три случая:

– система имеет одно решение;

– может не иметь ни одного решения;

– имеет бесчисленное множество решений.

В первом случае получаем одну неподвижную точку, во втором – отсутствие двойных точек, в третьем – прямолинейный ряд двойных точек, который принадлежит прямой линии, т.е. образуется двойная прямая (прямая неподвижных точек).

В последнем случае наблюдается пропорциональность коэффициентов:

.

Это обозначает, что оба уравнения (3.8) представляют собой одну и ту же прямую, все точки которой являются неподвижными. Этой прямой является ось перспективно-аффинного соответствия (см. п. 2.1.2).

3.5 Аффинная система координат в пространстве

Аффинная система координат в пространстве определяется координатным репером – четыре точки, не лежащие в одной плоскости, началом координат – точка и осями координат (рисунок 3.6):

Рисунок 3.6 – Аффинная система координат в пространстве

Аффинными координатами произвольной точки пространства называют три отношения:

, , .

Аффинными преобразованиями пространства называют все преобразования, которые в какой-либо (хотя бы в одной) аффинной системе координат записываются линейными уравнениями:

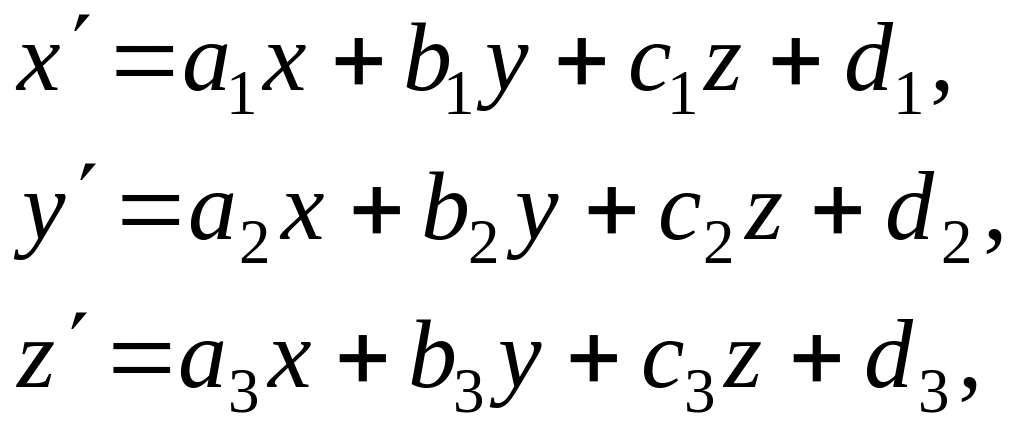(3.11)

для которых выполняется условие

.

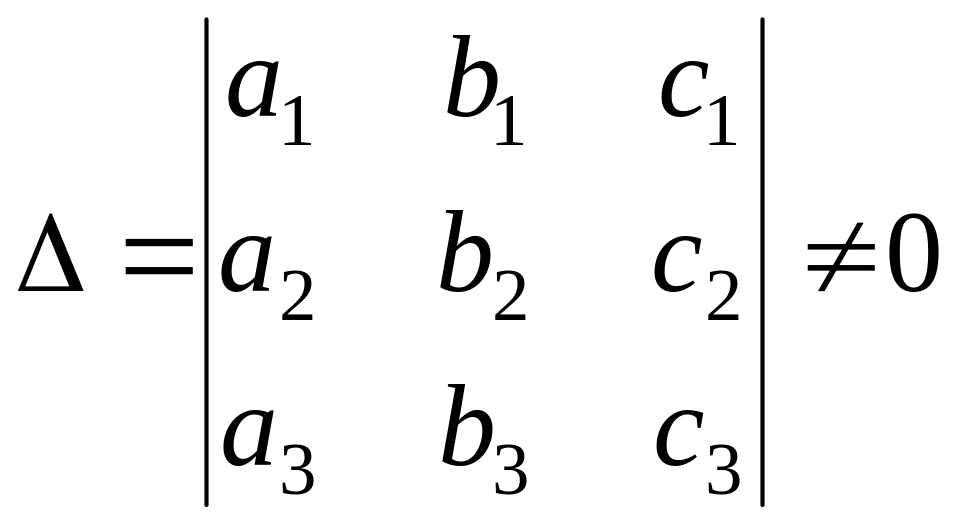Преобразования (3.11) переводят:

– точку в точку , т.е. ;

– плоскость

в плоскость

;

– параллельные плоскости

и

в параллельные плоскости

и ,

где

, , .

Аналогично аффинные преобразования (3.8) переводят прямую линию в прямую, параллельные прямые в параллельные; сохраняется отношение отрезков одной прямой или параллельных прямых.

Для данного трехмерного случая имеет место основная теорема теории аффинных преобразований в пространстве.

Теорема: существует одно и только одно аффинное преобразование пространства, переводящие данные четыре точки , не лежащие в одной плоскости, в четыре другие точки , также не лежащие в одной плоскости.

Следует отметить, что выражения (3.11) можно рассматривать и как формулы преобразования координат, аналогично тому, как это представлено для плоскости в подразд. 3.3.

С другими свойствами аффинных преобразований в пространстве можно познакомиться в изданиях [8, 11, 12, 15]. В частности одно отметим. Если аффинное преобразование пространства переводит какую-либо замкнутую поверхность в некоторую соответственную поверхность , то можно исследовать это преобразование одной поверхности в другую при помощи параллельных хорд, проведенных в первой поверхности по определенному направлению. Таким хордам будут соответствовать во второй поверхности также параллельные хорд, длины которых изменены в одном и том же отношении. Поэтому аффинное преобразование, переводящее поверхность в соответственную ей поверхность , можно охарактеризовать как сжатие или растяжение в определенном направлении [11].