Часть первая – основы аффинной геометрии

1 Отображения и преобразования

1.1 Современное определение геометрии

Выдающийся немецкий математик XIX века Ф. Клейн предложил определить геометрию как теорию инвариантов относительно той или иной группы преобразований плоскости (пространства). Эти идеи были представлены Клейном в 1872 г. перед ученым советом эрлангенского университета в докладе «Сравнительное обозрение новейших геометрических исследований», который он сделал при вступлении на должность профессора этого университета. В дальнейшем научные воззрения, изложенные в этой лекции, получили название Эрлангенской программы Клейна [5].

С тех пор определение геометрии основано на теоретически групповых принципах: геометрия – это наука, изучающая свойства фигур, неизменных (инвариантных) при выполнении преобразований, составляющих некоторую группу. Из этого следует, что геометрий ровно столько, сколько имеется различных групп преобразований. Поэтому для уяснения этого положения необходимо правильное представление о математических понятиях как «преобразование» и «группа преобразований».

1.2 Понятия отображения и преобразования

1.2.1 Отображения

Термин «отображение» тесно связанно понятием функции [6]. Рассмотрим это на примерах в соответствии с рисунками 1.1 – 1.6.

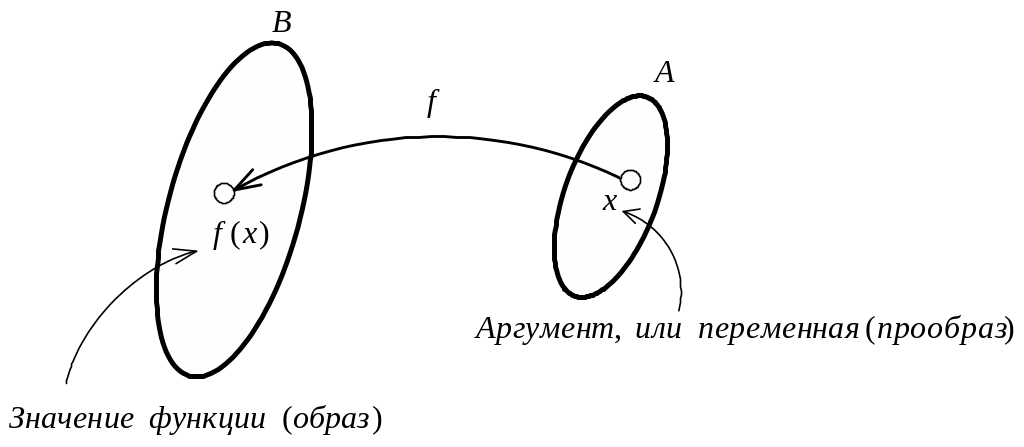
Рисунок 1.1 – Общее понятие об отображении

Здесь – элемент множества ; – область определения; – элемент множества ; – область значений.

При этом различают два случая отображения :

1) отображение множества множество ( ), см. рисунок 1.2.

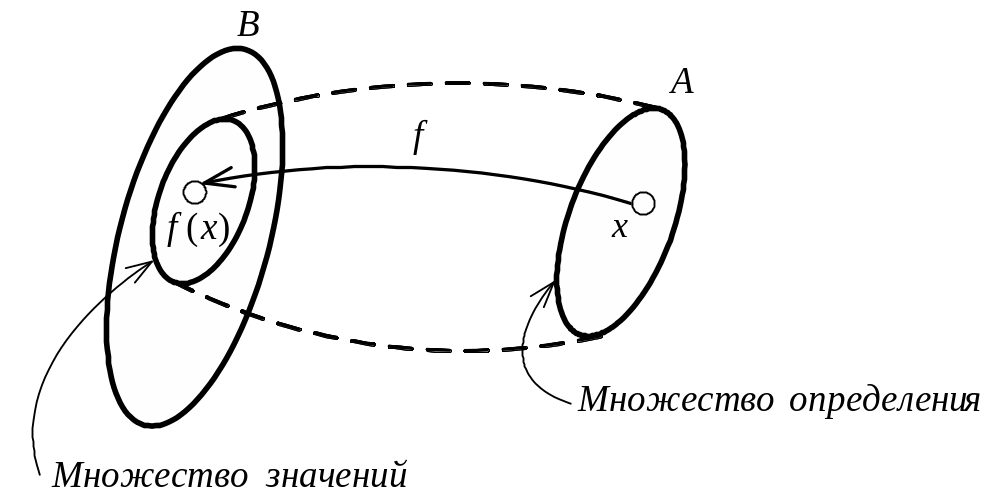
Рисунок 1.2 – Отображение множества множество ( )

2) отображение множества , или сюрьективное отображение (сюрьекция) см. рисунок 1.3.

Рисунок 1.3 – Отображение , или сюрьективное отображение

(сюрьекция)

Следует отметить, что функцию отображения называют прямой (или инъективной) функцией . Кроме того, различают и обратную функцию (рисунок 1.4).

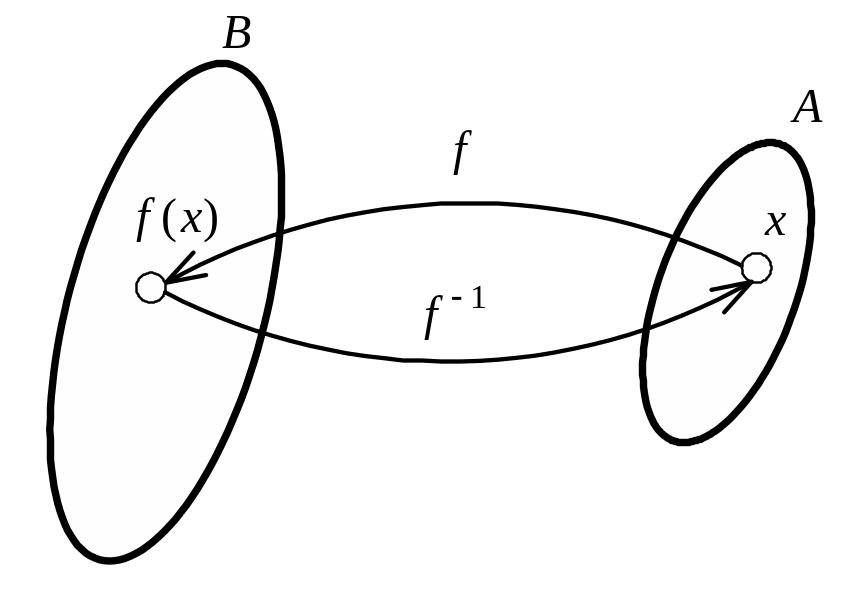
Рисунок 1.4 – Прямая (инъективная) функция отображения

и обратная функция ( )

Например, функция является прямой функцией , а функцией отображения , для данного примера служит выражение .

На рисунке 1.5 представлено инъективное отображение области в область .

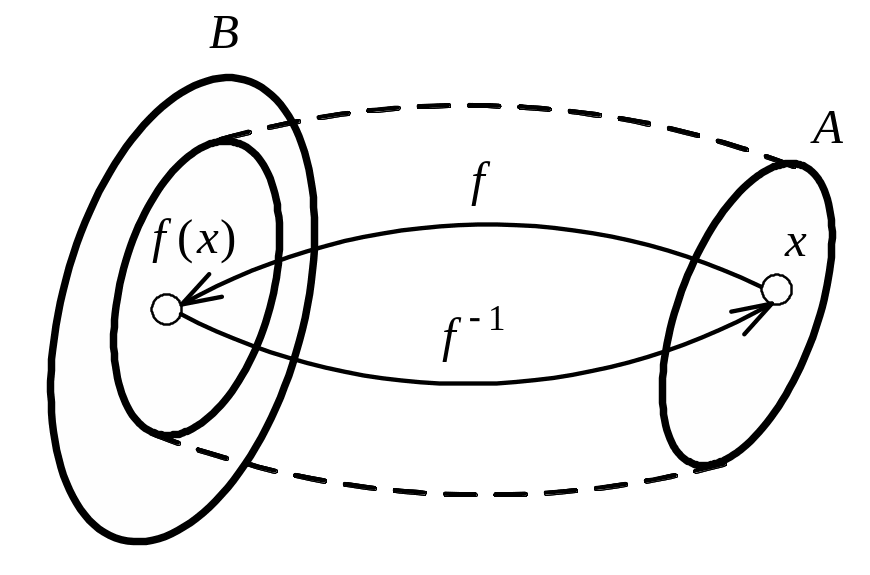
Рисунок 1.5 – Инъективное отображение, или инъекция

Кроме того, необходимо учитывать две особенности.

Первая особенность. Если для любого образа , множество преобразов состоит в точности из одного элемента , то называется взаимно-однозначным отображением или обратимым, или биективным, или биектцией (рисунок 1.6).

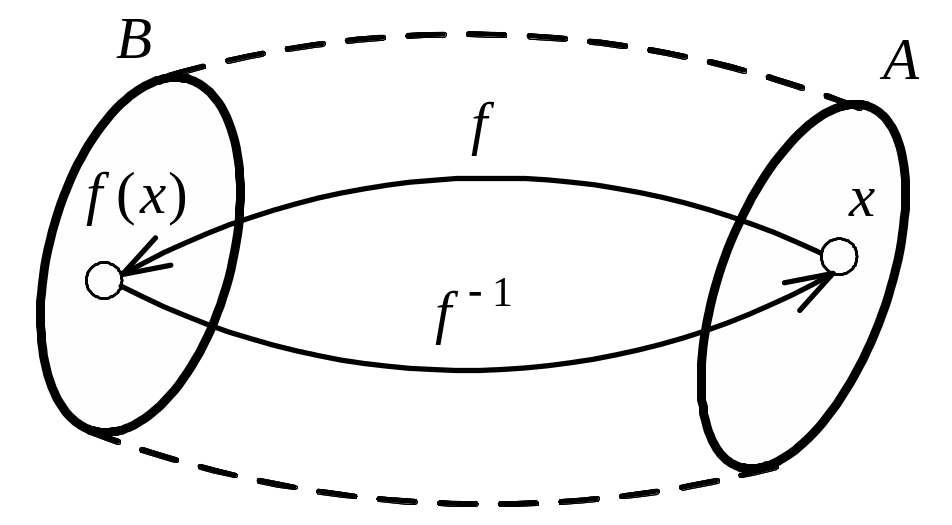
Рисунок 1.6 – Биективное отображение, или биекция

Вторая особенность. Если является обратимым отображением, то имеет место обратное отображение . В этом случае можно поменять местами области определения (отправления [7]) и значений (прибытия [7]). Обратимое отображение – это отображение ; отображение обратимым, т.е. взаимно однозначным, быть не может. Приведем несколько примеров [5].

Пример 1 – Одно-многозначное отображение (рисунок 1.7).

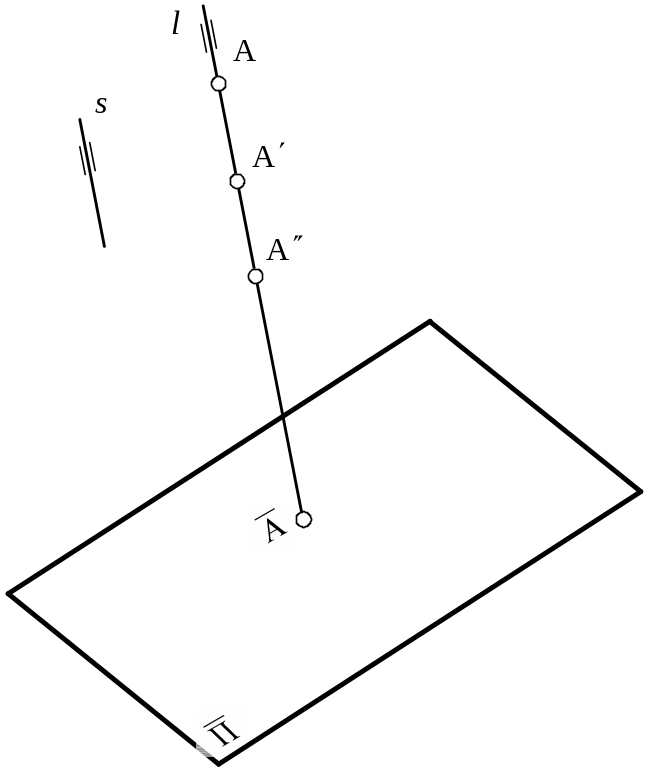
Рисунок 1.7 – Отображение точек трехмерного пространства на плоскость

В этом случае в точку проецируется не только точка , но и все точки ( ) проецирующей прямой .

Пример 2 – Взаимно однозначное отображение (рисунок 1.8).

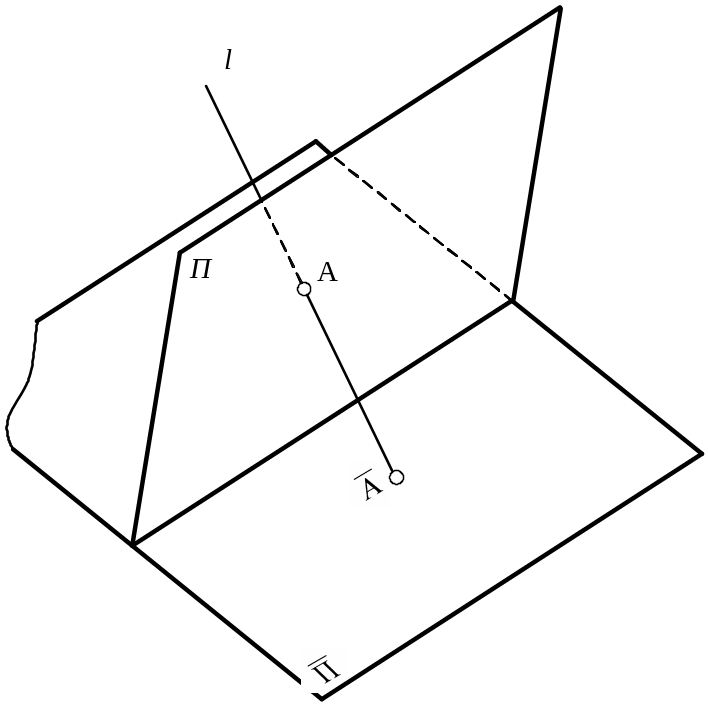
Рисунок 1.8 – Параллельное проецирование точек

двух плоскостей друг на друга

В данном случае при параллельном проецировании точек двух плоскостей и друг на друга отображение является обратимым отображением.

1.2.2 Преобразования

Взаимно однозначное отображение называется преобразованием , если область значений и область определения – одно и то же множество, т.е. они совмещены. Говорят, что это отображение множества на себя, или преобразование множества.

Когда рассматривают геометрическое преобразование, то подразумевают под множеством – множество точек плоскости (пространства).

Преобразования называют линейными, если образом прямой (плоскости) является также прямая (плоскость). Иначе преобразования называются нелинейными. В таком случае вводится понятие порядка преобразования. Порядок преобразования плоскости определяется порядком образа прямой линии, а преобразования пространства – порядком образа плоскости.

При выполнении преобразования, например плоскости, необходимо учитывать еще несколько важных аспектов:

– если какое-то свойство фигуры сохраняется в преобразовании , то фигура обладает тем же свойством, то это свойство называется инвариантом преобразования (например, в «школьной» или элементарной геометрии, изучаемое подобие фигур, сохраняет равенство углов);

– если некоторая точка (или фигура ) совпадает в преобразовании со своим образом, т.е. (или ), то эта точка (или фигура ) переходит сама в себя, т.е. остается на месте и является неподвижной, или, еще говорят, двойной, или инвариантной точкой (фигурой) преобразования ;

– если в преобразовании образ фигуры не изменяет ориентации на противоположную, то преобразование является преобразованием 1-го рода (например, трансляция, или параллельный перенос); в противном случае имеем дело с преобразованием 2-го рода (например, центровая и осевая симметрии);

– если любая фигура в преобразовании переходит в себя, т.е. или , то такое преобразование называется тождественным.

– если для преобразования имеет место , т.е. преобразование, совпадающее со своим обратным, то такое преобразование называется инволюционным, или инволюцией (например, центральная и осевая симметрии).

Подытожим сказанное: математический термин «преобразование» используется лишь в случае взаимно однозначных отображений. Если же рассматриваются многозначные соответствия, когда одной точке первого поля соответствуют несколько точек второго поля и обратно, то необходимо использовать термин «соответствие» [5].