
4. Используя правило f(r),
а) зададим бинарное отношение R
- списком:
а1 R а6 |
а2 R а6 а2 R а7 |
а3 R а2 а3 R а7 |
а4R а3 а4 R а5 а4 R а6 а4 R а7
|
а5 R а6
|
а7 R а5 а7 R а6
|
а8 R а1 а8 R а5 а8 R а6 а8 R а7
|
а9 R а1 а9 R а2 а9 R а3 а9 R а5 а9 R а6 а9 R а7 а9 R а8 |
- матрицей:
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
a2 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
a3 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
a4 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
a5 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
a6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
a7 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
a8 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
a9 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
-
a1
a2
графом:a9

a3
a4
a8
a7
a5
a6
б) построим диаграмму Вена для исследуемого бинарного отношения R (рис.1).
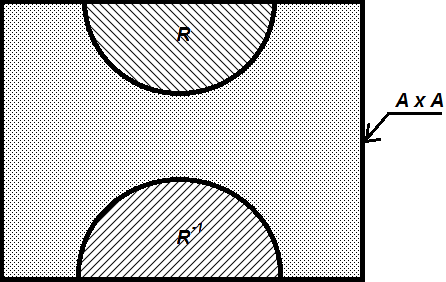
А×А
Рис. 1 – диаграмма Вена для исследуемого бинарного отношения
Проанализируем и докажем справедливость (или несправедливость) свойств бинарных отношений для исследуемого бинарного отношения R.
а) Рефлексивность
Рассматриваемое отношение нерефлексивно, т.к. вершины графа не имеют петель, на главной диагонали матрицы стоят не единицы.
б) Антирефлексивность
Рассматриваемое отношение антирефлексивно, т.к. вершины графа не имеют петель и на главной диагонали матрицы стоят нули.
в) Симметричность
Рассматриваемое отношение несимметрично, т.к. граф не содержит встречных дуг.
г) Асимметричность
Свойство асимметричности выполняется для рассматриваемого отношения, т.к. граф не содержит встречных дуг и петель и отношение антирефлексивно.
д) Антисимметричность
Свойство антисимметричности не выполняется для рассматриваемого отношения, т.к. граф не содержит петель.
е) Транзитивность
Рассматриваемое отношение является транзитивным. Любая пара последовательно расположенных дуг, образующих путь, замыкается дугой того же направления. Также рассматриваемое отношение является транзитивным, т.к. матрицу можно привести к треугольному виду:
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a1 |
0 |
|
|
|
|
1 |
|
|
|
a2 |
|
0 |
|
|
|
1 |
1 |
|
|
a3 |
|
1 |
0 |
|
|
|
1 |
|
|
a4 |
|
|
1 |
0 |
1 |
1 |
1 |
|
|
a5 |
|
|
|
|
0 |
1 |
|
|
|
a6 |
|
|
|
|
|
0 |
|
|
|
a7 |
|
|
|
|
1 |
1 |
0 |
|
|
a8 |
1 |
|
|
|
1 |
1 |
1 |
0 |
|
a9 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
1.Поменяем местами столбцы и строки a9 и a6.
|
a1 |
a2 |
a3 |
a4 |
a5 |
a9 |
a7 |
a8 |
a6 |
a1 |
0 |
|
|
|
|
|
|
|
1 |
a2 |
|
0 |
|
|
|
|
1 |
|
1 |
a3 |
|
1 |
0 |
|
|
|
1 |
|
|
a4 |
|
|
1 |
0 |
1 |
|
1 |
|
1 |
a5 |
|
|
|
|
0 |
|
|
|
1 |
a9 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
a7 |
|
|
|
|
1 |
|
0 |
|
1 |
a8 |
1 |
|
|
|
1 |
|
1 |
0 |
1 |
a6 |
|
|
|
|
|
|
|
|
0 |
2.Поменяем местами столбцы и строки a9 и a1.
|
a9 |
a2 |
a3 |
a4 |
a5 |
a1 |
a7 |
a8 |
a6 |
a9 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
a2 |
|
0 |
|
|
|
|
1 |
|
1 |
a3 |
|
1 |
0 |
|
|
|
1 |
|
|
a4 |
|
|
1 |
0 |
1 |
|
1 |
|
1 |
a5 |
|
|
|
|
0 |
|
|
|
1 |
a1 |
|
|
|
|
|
0 |
|
|
1 |
a7 |
|
|
|
|
1 |
|
0 |
|
1 |
a8 |
|
|
|
|
1 |
1 |
1 |
0 |
1 |
a6 |
|
|
|
|
|
|
|
|
0 |
3.Поменяем местами столбцы и строки a8 и a2.
|
a9 |
a8 |
a3 |
a4 |
a5 |
a1 |
a7 |
a2 |
a6 |
a9 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
a8 |
|
0 |
|
|
1 |
1 |
1 |
|
1 |
a3 |
|
|
0 |
|
|
|
1 |
1 |
|
a4 |
|
|
1 |
0 |
1 |
|
1 |
|
1 |
a5 |
|
|
|
|
0 |
|
|
|
1 |
a1 |
|
|
|
|
|
0 |
|
|
1 |
a7 |
|
|
|
|
1 |
|
0 |
|
1 |
a2 |
|
|
|
|
|
|
1 |
0 |
1 |
a6 |
|
|
|
|
|
|
|
|
0 |
4.Поменяем местами столбцы и строки a2 и a5.
|
a9 |
a8 |
a3 |
a4 |
a2 |
a1 |
a7 |
a5 |
a6 |
a9 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
a8 |
|
0 |
|
|
|
1 |
1 |
1 |
1 |
a3 |
|
|
0 |
|
1 |
|
1 |
|
|
a4 |
|
|
1 |
0 |
|
|
1 |
1 |
1 |
a2 |
|
|
|
|
0 |
|
1 |
0 |
1 |
a1 |
|
|
|
|
|
0 |
|
|
1 |
a7 |
|
|
|
|
|
|
0 |
1 |
1 |
a5 |
|
|
|
|
|
|
|
0 |
1 |
a6 |
|
|
|
|
|
|
|
|
0 |
5.Поменяем местами столбцы и строки a8 и a4.
|
a9 |
a4 |
a3 |
a8 |
a2 |
a1 |
a7 |
a5 |
a6 |
a9 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
a4 |
|
0 |
1 |
|
|
|
1 |
1 |
1 |
a3 |
|
|
0 |
|
1 |
|
1 |
|
|
a8 |
|
|
|
0 |
|
1 |
1 |
1 |
1 |
a2 |
|
|
|
|
0 |
|
1 |
|
1 |
a1 |
|
|
|
|
|
0 |
|
|
1 |
a7 |
|
|
|
|
|
|
0 |
1 |
1 |
a5 |
|
|
|
|
|
|
|
0 |
1 |
a6 |
|
|
|
|
|
|
|
|
0 |
ж) Линейность
Рассматриваемое отношение не обладает свойством линейности, т.к. не все вершины графа соединены дугой либо парой встречных дуг.
Вывод по исследованию бинарного отношения.
Рассматриваемое отношение обладает свойствами антирефлексивности, асимметричности и транзитивности, следовательно, это отношение частичного строгого порядка.
