
МИНОБР НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Тульский государственный университет
Кафедра робототехники и автоматизации производства
Лабораторные работы
Вариант 7.
Проверил: Мозжечков В.А.
Выполнил: ст. гр. 220391 Кугилевич Е.И.
Тула 2012
Лабораторная работа №1
Моделирование процессов управления в электроприводе с
регулированием скорости по разомкнутому контуру на основе
решения дифференциальных уравнений
ЦЕЛЬ РАБОТЫ: получение навыков моделирования систем управления путем решения численным методом на ЭВМ обыкновенных дифференциальных уравнений, описывающих поведение исследуемой системы, на примере моделирование процессов управления в электроприводе с пропорциональным регулированием положения выходного звена.
Функциональная cхема, отражающая моделируемую систему.
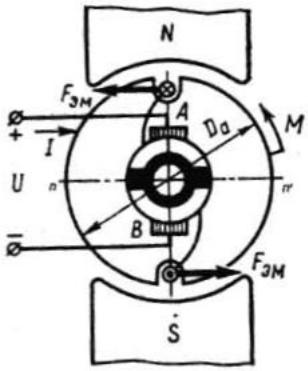
3. Уравнения, составляющие описание системы, в исходной форме и в
нормальной форме Коши.
U=iR+Ldi/dt+ωCe,
Mдв=Jdω/dt+Mнагр,
Mдв=iCm,
U=uk
В нормальной форме Коши:
di/dt=(uk-iR-ωCe)/L
dω/dt=(iCm-Mнагр)/J4.
Значения параметров и начальных условий.
Для варианта номер 7:
R=(1+0.05*7)=1.35 Ом,
Jпр=(2*10-5+7*5*10-7)=2.35 кг/м2,
L=(0.1+0.005*7)=0.135 Гн,
Mнагр=(0.01+7·5*10-4)=0.0135 нм,
Ce=(0.05+7*5*10-4)=0.0535 В·c/рад,
k=1,
Cm=(0.05+7*5*10-4)=0.0535 нм/a,
u=27В,
Начальные условия
i=0 А
ώ=0 рад/сек.
Текст программы.
unit Mylab1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ExtCtrls, StdCtrls, Grids;
type
TForm1 = class(TForm)
Button1: TButton;
StringGrid1: TStringGrid;
procedure Button1Click(Sender: TObject);
procedure decart;
procedure FormCreate(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
procedure tform1.decart;
var
i:integer;
begin
with canvas do begin
brush.Color:=clgray;
fillrect(rect(0,120,width,height));
pen.Color:=clblack;
moveto(100,20);
lineto(100,580);
moveto(20,300);
lineto(605,300);
for i:=0 to 22 do begin
moveto(50+25*i,305);
lineto(50+25*i,295);
if i<> 2 then textout(46+25*i,312,currtostr(-0.5+i/4));
end;
for i:=1 to 50 do begin
moveto(105,20+20*i);
lineto(95,20+20*i);
end;
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
var
di,dt,dw,i,w,cm,m,r,ce,u,l,j:real;
n,q:integer;
begin
r:=(1+0.05*n);
l:=(0.1+0.005*n);
ce:=(0.05+n*0.0005);
cm:=ce;
j:=(0.00002+n*0.0000005);
m:=(0.01+n*0.0005);
u:=27;
decart;
Canvas.MoveTo(100,300);
Canvas.Pen.Color:=clblack;
i:=0;
w:=0;
for q:=0 to 2500 do
begin
di:=((u - i*r-w*ce)/l)*dt;
dw:=((i*cm-M)/j)*dt;
i:=i+di;
w:=w+dw;
Canvas.lineTo(round(q/5)+100,300-round(20*i));
if (q mod 100 =0) then
begin
stringgrid1.Cells[0,1+q div 100]:= currtostr(q/500);
stringgrid1.Cells[1,1+q div 100]:= currtostr(i);
stringgrid1.Cells[2,1+q div 100]:= currtostr(w);
end;
end;
Canvas.MoveTo(100,300);
Canvas.Pen.Color:=clwhite;
i:=0;
w:=0;
for q:=0 to 2500 do
begin
di:=((u - i*r-w*ce)/l)*dt;
dw:=((i*cm-M)/j)*dt;
i:=i+di;
w:=w+dw;
Canvas.lineTo(round(q/5)+100,300-round(w/5));
end;
showmessage ('i = '+currtostr(i)+' A'+#13+ 'w = '+currtostr(w)+ ' rad/sec');
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
stringgrid1.Cells[0,0]:='t (cek)';
stringgrid1.Cells[1,0]:='i (Amp)';
stringgrid1.Cells[2,0]:='w (rad/cek)';
end;
end.
Таблица результатов моделирования.

7. Графики I(t),w(t)

8. Уточненное значение Δt.
Δt=0.0009 секунды
9. Аналитические зависимости для определения установившихся значений i и ω.
![]()
![]()
10. Установившиеся значения i и ω, полученные из аналитических
зависимостей и из таблицы результатов моделирования.
i=0.2522 А
ω= 498.3168 рад/c
11. Определите величину перерегулирования скорости из графика ω(t).
Перерегулирование примерно равно
![]()
Лабораторная работа №2
Моделирование процессов управления в электроприводе
с пропорциональным регулированием положения выходного
вала на основе решения дифференциальных уравнений
ЦЕЛЬ РАБОТЫ: получение навыков моделирования систем управления путем решения численным методом на ЭВМ обыкновенных дифференциальных уравнений, описывающих поведение исследуемой системы, на примере моделирование процессов управления в электроприводе с пропорциональным регулированием положения выходного звена.
2. Функциональная cхема, отражающая моделируемую систему.
3 . Уравнения, составляющие описание моделируемой системы.
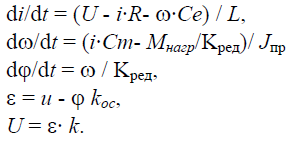
4. Значения параметров и начальных условий.
Для варианта номер 7:
R = (1 +0.05*7)=1.35 Ом,
Jпр = (2*10 - 5 +7·5*10 - 8 )=2.35 кг·м2,
L = (0.1 +0.005*1) =0.105 Гн,
Mнагр = (0.01 +7·5*10 -4)=0.0135 Нм,
Ce = (0.05 +7·5*10 - 4 ) =0.0535 В·c/рад,
k = 1,
Cm = (0.05+ 7·5*10-4 ) =0.0535 Нм/A,
u = 1 В,
Kред = 10,
kос = 1 В/рад .
Начальные условия
i=0 А
φ=0 рад
ώ=0 рад/сек.
5. Текст программы.
unit Mylab2;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, Grids, StdCtrls;
type
TForm1 = class(TForm)
StringGrid1: TStringGrid;
Button1: TButton;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
procedure TForm1.Button1Click(Sender: TObject);
var
n,r,l,ce,cm,j,m,k,kr,koc,u,i,w,f,e,di,dw,df,dt:real;
a:integer;
begin
n:=7;
dt:=0.0001;
r:=1+0.05*n;
L:=0.1+0.005*n;
m:=0.01+0.0005*n;
ce:=0.05+0.0005*n;
cm:=0.05+0.0005*n;
j:=0.00002+0.0000005*n;
k:=1;
kr:=10;
koc:=1;
u:=1;
i:=0;
w:=0;
f:=0;
e:=0;
Canvas.Brush.Color:=clgray;
Canvas.Rectangle(50,50,650,400);
Canvas.Pen.Color:=clBlack;
Canvas.Pen.Style:=psSolid;
for a:=1 to 11 do
begin
Canvas.MoveTo(50*a+50,50);
Canvas.LineTo(50*a+50,400);
Canvas.TextOut(50*a+40,305,FloatToStr((a-1)*0.25));
if a=11 then Canvas.TextOut(50*(a+1)+60,305,'t');
end;
for a:=1 to 6 do
begin
Canvas.MoveTo(50,50*a+50);
Canvas.LineTo(650,50*a+50);
end;
Canvas.Pen.Style:=psSolid;
Canvas.Pen.Width:=2;
Canvas.MoveTo(100,50);
Canvas.LineTo(100,400);
Canvas.MoveTo(50,300);
Canvas.LineTo(650,300);
Canvas.Pen.Color:=clgreen;
Canvas.TextOut(70,55,'i(t)');
Canvas.MoveTo(70,70);
Canvas.LineTo(80,70);
Canvas.MoveTo(100,300);
for a:=0 to 25000 do
begin
Canvas.LineTo(Trunc(a/50)+100,300-Round(200*i));
StringGrid1.Cells[0,0]:='T,сek';
StringGrid1.Cells[1,0]:='I,Аmper';
StringGrid1.Cells[2,0]:='W,rad/cek';
StringGrid1.Cells[3,0]:='F,rad';
StringGrid1.Cells[4,0]:='E';
if (a mod 625=0) then
begin
StringGrid1.Cells[0,1+a div 625]:=FloatToStr(a/10000);
StringGrid1.Cells[1,1+a div 625]:=FloatToStrF(i,ffFixed,7,3);
StringGrid1.Cells[2,1+a div 625]:=FloatToStrF(w,ffFixed,7,3);
StringGrid1.Cells[3,1+a div 625]:=FloatToStrF(f,ffFixed,7,3);
StringGrid1.Cells[4,1+a div 625]:=FloatToStrF(e,ffFixed,7,3);
end;
e:=u-f*koc;
di:=((e*k-i*r-w*ce)/l)*dt;
dw:=((i*cm-m/kr)/j)*dt;
df:=(w/kr)*dt;
i:=i+di;
w:=w+dw;
f:=f+df;
end;
i:=0;
w:=0;
f:=0;
Canvas.Pen.Color:=clWhite;
Canvas.TextOut(70,75,'w(t)');
Canvas.MoveTo(70,90);
Canvas.LineTo(80,90);
Canvas.MoveTo(100,300);
for a:=0 to 25000 do
begin
Canvas.LineTo(Trunc(a/50)+100,300-Round(w*7));
e:=u-f*koc;
di:=((e*k-i*r-w*ce)/l)*dt;
dw:=((i*cm-m/kr)/j)*dt;
df:=(w/kr)*dt;
i:=i+di;
w:=w+dw;
f:=f+df;
end;
i:=0;
w:=0;
f:=0;
Canvas.Pen.Color:=clBlack;
Canvas.TextOut(70,95,'f(t)');
Canvas.MoveTo(70,110);
Canvas.LineTo(80,110);
Canvas.MoveTo(100,300);
for a:=0 to 25000 do
begin
Canvas.LineTo(Trunc(a/50)+100,300-Round(50*f));
e:=u-f*koc;
di:=((e*k-i*r-w*ce)/l)*dt;
dw:=((i*cm-m/kr)/j)*dt;
df:=(w/kr)*dt;
i:=i+di;
w:=w+dw;
f:=f+df;
end;
showmessage ('i = '+currtostr(i)+' A'+#13+ 'w = '+currtostr(w)+ ' rad/sec'+#13+'f='+currtostr(f)+' rad');
end;
end.
Таблица результатов моделирования.

