1.4 Вибір оптимального маршруту

Враховуючи те, що круїз е круговим, в якості методу оптимізації обираємо методи рішення «задачі комівояжера».

Постановка завдання задачі комівояжера полягає в наступному.

Мається 8 портів, відстані між ними (табл.1) задані у вигляді матриці

C = (cij), де i.j = ( 1…n ). В таблиці 1 кожному порту призначено номер від одиниці до восьми.

Таблиця 1 Відстані між портами лінії

Порти виходу	Порти заходу
	Одесса	Афины	Неаполь	Барселона	Валлетта	Алек-я	Хайфа	Стамбул
Одеса (1)		652	1314	1800	1204	1077	1184	298
Афіни (2)	652		737	1323	626	519	285	354
Неаполь (3)	1314	737		558	325	999	1270	971
Барселона (4)	1800	1323	558		671	1472	1750	1487
Валлетта (5)	1204	626	325	671		818	1033	860
Александрія (6)	1077	519	999	1472	818		235	733
Хайфа (7)	1184	285	1270	1750	1033	235		247
Стамбул (8)	298	354	971	1467	860	733	247

Кожне значення cij є відстанями між вихідним портом i та портом заходу j, тому їх величини не можуть мати від’ємного значення, тому cij 0, .

В загальному випадку cij cji ( на приклад коли cji є вартість проїзду з міста j в місто i, яке не дорівнює переїзду з міста i в місто j ). Така задача вважається несиметричною. Враховуючи особливості роботи морського транспорту та географічне розташування портів круїзу, наша задача має симетричний характер, тобто cij = cji.

Треба знайти найратчайший замкнутий маршрут, який проходить через кожен порт тільки один раз с поверненням в перший базовий порт і який мінімізує сумарну пройдену відстань.

Математична постанова завдання може бути представлена в наступному вигляді:

; (1)

(2)

(3)

Xij (4)

Визначення. Матриця С має назву приведеної , коли усі її елементи невід’ємні, а кожен рядок та стовбець містить хоча б один нуль.

Приведення матриці С може бути здійснено наступним чином.

Крок1-Приведення по строкам. По кожній строчці і знайдемо найменший елемент min Cij = ai. Тоді при переході до приведеної матриці . Ця операція потребує , на наш погляд, пояснень. Здавалось би логічним . виключати найбілішу відстань згідно з умовами постанови задачі, але у такому випадку всі останні елементи строчки будуть мати від’ємні значення, що порушує обмеження (4). Обрані значення ai відображаються у заключному стовбці приведеної матриці табл.2.

Крок 2. У кожному стовбці j, який не має нульових елементів знаходимо найменше значення Cij= bj, яке відображаємо у заключній строчці bj приведеної матриці ,табл..3.

Тоді Результати першого кроку відображено в табл..2

Табл.2 Матриця, приведена по рядках (строках)

	1	2	3	4	5	6	7	8	ai
1		354	1016	1502	906	779	886	0	298
2	367		452	1038	341	234	0	69	285
3	989	412		233	0	674	945	646	325
4	1242	765	0		113	914	1192	909	558
5	879	301	0	346		493	708	535	325
6	842	284	764	1237	583		0	498	235
7	949	50	1035	1515	798	0		12	235
8	51	107	724	1220	613	486	0		247
bj									2508

Результати кроку 2 відображено в табл.3, яка представляє першу приведену матрицю G0.

Табл.3 Приведена матриця G0

	1	2	3	4	5	6	7	8	ai
1		304	1016	1269	906	779	886	0 - 316	298
2	316		452	805	341	234	0 - 69	69	285
3	938	362		0 - 113	0-113	674	945	646	325
4	1191	715	0-113		113	914	1192	909	558
5	828	251	0-113	113		493	708	535	325
6	791	234	764	1004	583		0-234	498	235
7	898	0 - 57	1035	1282	798	0-234		12	235
8	0-316	57	724	987	613	486	0 - 0		247
bj	51	50	0	233	0	0	0	0	2842

Згідно з теоремою Ейлера, яка стверджує, що коли ми відраховуємо любу константу із усіх елементів строки чи стовпця матриці Сij, ми залишаємо мінімальний тур мінімальним.

На пересечінні ітогової строки i та стовбця j знаходиться величина, яка має назву – «сума приводящих констант», яка дорівнює:

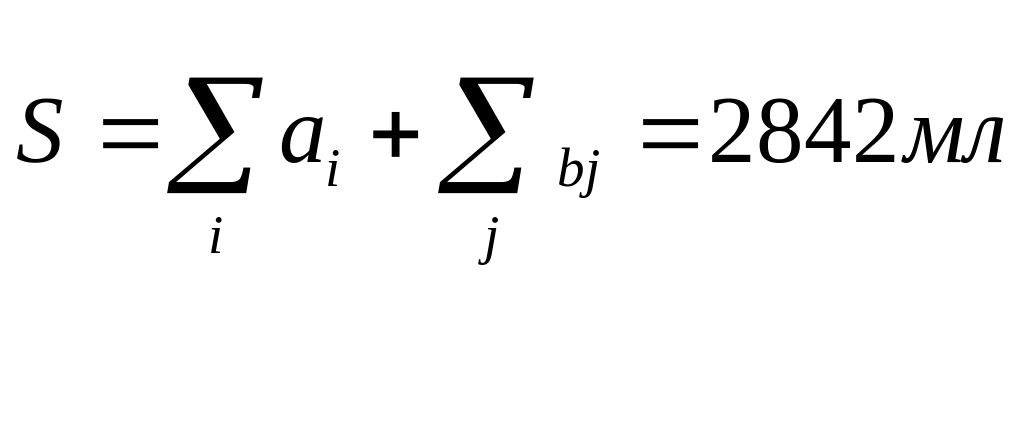(4)

Дані, наведені у таблиці 3, визначимо як матрицю G0, що визначає нову задачу комівояжера, яка в якості оптимального варіанту має ту саму послідовність портів.

Між величинами L , існує наступне співвідношення.

L= + S (5)

Таким чином, L , що визначає S як нижню межу цільової функції задачі комівояжера.

Знаходимо ступені кожного з нулів повністю приведеної матриці.

Для цього для кожної клітки з нульовим елементом по відповідним строчці та стовбцю знаходимо мінімальні значення Сij. Сума цих елементів визначить ступінь нулю, яка записана через дефіс поряд з нулем праворуч.

Клітка з максимальною ступеню нуля визначить дугу, згідно з якою буде виконуватись подальше гілкування.

Визначаємо максимальний ступінь нуля. Вона рівна 316 і відповідає кліткам (1-8) і (8-1). Обираємо клітку (1-8). Таким чином, претендентом на включення в гамільтонов контур є дуга (1-8).

Розбиваємо безліч всіх гамільтонових контурів на дві підмножини: G1 і G2. Матрицю з дугою (1-8) одержуємо шляхом викреслювання рядка 1 і стовпця 8 (табл.4). Щоб не допускати утворення негамільтонового контуру (зациклювання), замінюємо елемент (8-1) на знак « ».

Таблиця 4 Матриця G1 (включає дугу 1-8)

	1	2	3	4	5	6	7
2	316		452	805	341	234	0
3	938	362		0	0	674	945
4	1191	715	0		113	914	1192
5	828	251	0	113		493	708
6	791	234	764	1004	583		0
7	898	0	1035	1282	798	0
8		57	724	987	613	486	0

Підмножина G2, навпаки, виключає дугу (1-8). Для цього замінюємо елемент (1-8) в таблиці 3 на знак « ». Матриця G2 відображена в таблиці 5.

Графічно це показано на рис.1.

Таблиця 5 Матриця G2 (виключає дугу 1-8)

	1	2	3	4	5	6	7	8
1		304	1016	1269	906	779	886
2	316		452	805	341	234	0	69
3	938	362		0	0	674	945	646
4	1191	715	0		113	914	1192	909
5	828	251	0	113		493	708	535
6	791	234	764	1004	583		0	498
7	898	0	1035	1282	798	0		12
8	0	57	724	987	613	486	0

Подальше гілкування почнемо з підмножини G1.

Виконуємо приведення матриці G1 за алгоритмом, який було приведено вище.

Результати приведення наведено в таблиці 6.

Таблиця 6 Приведена матриця G1 (з дугою 1-8)

	1	2	3	4	5	6	7	ai
2	0-475		452	805	341	234	0	0
3	622	362		0-113	0-113	674	945	0
4	876	715	0-113		113	914	1192	0
5	512	251	0-113	113	22	493	708	0
6	475	234	764	1004	583		0-234	0
7	582	0-57	1035	1282	798	0-234		0
8		57	724	987	613	486	0-57	0
bj	316	0	0	0	0	0	0	316

Як видно з таблиці 6 приведена константа для підмножини G1 дорівнює 316. Тоді нижча границя гамільтонових контурів для цієї підмножини буде складати:

S(G1)=2842+316 = 3158

Зробимо приведення матриці G2. Результати наведено в таблиці 7.

Таблиця 7 Приведена матриця G2 (виключає дугу 1-8)

	1	2	3	4	5	6	7	8	ai
1		0	712	965	602	475	582		304
2	316		452	805	341	234	0	69	0
3	938	362		0	0	674	945	646	0
4	1191	715	0		113	914	1192	909	0
5	828	251	0	113		493	708	535	0
6	791	234	764	1004	583		0	498	0
7	898	0	1035	1282	798	0		12	0
8	0	57	724	987	613	486	0		0
bj	0	0	0	0	0	0	0	12	316

Приведена константа для підмножини G2 також дорівнює 316. Тоді нижча границя гамільтонових контурів для цієї підмножини буде складати

S(G2)=2842+316 = 3158

Порівняв значення нижніх границь (рекордів) для підмножин G1 і G2 робимо висновок, що подальшому гілкуванню підлягають обидві підмножини.

Продовжимо гілкування множини G1. Оцінимо клітки з «0». Найвищу оцінку має дуга (2-1). Розглядаємо її як елемент майбутньої можливої оптимальної схеми. Таким чином ми маємо дві дуги, а саме: (1-8) і (2-1). Або схему руху (2-1-8). Виключаючи зациклювання заборонимо рух по дузі (8-2) значком « ». Розіб’ємо множину G1 на підмножини G3 (включає дугу 2-1) і G4 (забороняє рух по дузі 2-1)

Таблиця 8 Матриця G3 (включає дугу 2,1)

	2	3	4	5	6	7
3	362		0	0	674	945
4	715	0		113	914	1192
5	251	0	113	22	493	708
6	234	764	1004	583		0
7	0	1035	1282	798	0
8		724	987	613	486	0

Підмножину G4 отримуємо з таблиці 6, заборонив рух по дузі (2,1) знаком « ».

Таблиця 9 Матриця G4 (виключає дугу 2,1)

	1	2	3	4	5	6	7
2			452	805	341	234	0
3	622	362		0	0	674	945
4	876	715	0		113	914	1192
5	512	251	0	113	22	493	708
6	475	234	764	1004	583		0
7	582	0	1035	1282	798	0
8		57	724	987	613	486	0

Зробимо приведення матриць G3 і G4.

Таблиця 10 Приведена матриця G3

	2	3	4	5	6	7	ai
3	362		0 -113	0-113	674	945	0
4	715	0 - 113		113	914	1192	0
5	251	0 -113	113	22	493	708	0
6	234	764	1004	583		0-234	0
7	0 -234	1035	1282	798	0-486		0
8		724	987	613	486	0	0
bj	0	0	0	0	0	0	0

Приведена константа для підмножини G3 дорівнює 0. Тоді нижча границя гамільтонових контурів для цієї підмножини буде складати

S(G3) = 3158 + 0 = 3158

Таблиця 11 Приведена матриця G4

	1	2	3	4	5	6	7	ai
2			452	805	341	234	0	0
3	622	362		0	0	674	945	0
4	876	715	0		113	914	1192	0
5	512	251	0	113	22	493	708	0
6	475	234	764	1004	583		0	0
7	582	0	1035	1282	798	0		0
8		57	724	987	613	486	0	0
bj	475	0	0	0	0	0	0	475

Приведена константа для підмножини G4 дорівнює 475. Тоді нижча границя гамільтонових контурів для цієї підмножини буде складати

S(G4)=3158 + 475 = 3633

Для подальшого гілкування обираємо множину G3. Множина G4 з подальшого розгляду виключається. В приведеній матриці G3 (табл..10) оцінимо «0». Дуга (7-6) розглядається як елемент схеми. Розіб’ємо G3 на G5 (включає дугу 7-6) і G6 виключає дугу 7-6).

Виконаємо аналогічні попереднім операції.

Табл.12 Приведена матриця G5 (включає дугу 7-6)

	2	3	4	5	7	ai
3	362		0-113	0-113	945	0
4	715	0-113		113	1192	0
5	251	0-113	113	22	708	0
6	0-600	530	770	349		0
8	@	724	987	613	0-1321	0
bj	0	0	0	0	0	0

Матрицю G6 отримаємо з табл.10 шляхом виключення дуги (7-6) знаком « ».

Порівняв приведені константи для множин G5 і G6 для подальшого гілкування обираємо множину G5, для якої S(G5) = 3158 + 0 = 31583. Розіб’ємо G5 на підмножини G7 і G8. З приведеної матриці G5, після оцінювання нульових кліток до включення в схему обираємо дугу (8-7). Таким чином отримуємо гамільтонов контур 2-1-8-7-6.

Табл.13 Матриця G6 (виключає дугу 7-6)

	2	3	4	5	6	7	ai
3	362		0	0	674	945	0
4	715	0		113	914	1192	0
5	251	0	113	22	493	708	0
6	234	764	1004	583		0	0
7	0	1035	1282	798			0
8		724	987	613	486	0	0
bj	0	0	0	0	486	0	486

Матрицю G7 отримаємо з таблиці 12 шляхом вилучення строки 8 і стовбця 7. Для запобігання за циклювання заборонимо дугу (6-2).

Таблиця 14 Приведена матриця G7

	2	3	4	5	ai
3	362	2	0-113	0-0	0
4	715	0 -113	2	113	0
5	251	0 - 113	113	222	0
6	2	181	421	0 -181	0
bj	251	0	0	0	251

Таблиця 15 Приведена матриця G8

	2	3	4	5	7	ai
3	362		0	0	945	0
4	715	0		113	1192	0
5	251	0	113	22	708	0
6	0	530	770	349		0
8	@	724	987	613		0
bj	0	0	0	0	708	708

S(G7)=3158 + 251 = 3409

S(G2)=3158 + 708 = 3866

Для подальшого розгляду обираємо підмножину G7. Оцінив нульові клітини до схеми залучаємо дугу (6-5). Розбиваємо G7 на G9 і G10 за тим ж самими правилами.

Таблиця 16 Приведена матриця G9

	2	3	4	ai
3	362	2	0-475	0
4	715	0 -715	2	0
5	2	0 -113	113	0
bj	362	0	0	362

Таблиця 17 Приведена матриця G10

	2	3	4	5	ai
3	362	2	0	0	0
4	715	0	2	113	0
5		0	113	2	0
6		181	421	2	0
bj	362	0	0	0	362

Оцінюємо нульові клітки в таблиці 16 і , як наслідок, обираємо до включення в схему дугу (4-3).

Гілкуванню підлягає множина G9, яка має S(G9) =3409 + 362 = 3771. Ми отримали матрицю розміром 2 х 2 (таблиця 18) і на цьому гілкування закінчується. До схеми включаються дуги (5-4) і (3-2).

Таблиця 18. Остання матриця

	2	4
3	362
5	2	113

Таким чином, отримано гамільтонов цикл: 1-8-7-6-5-4-3-2-1.

Круїзна лінія: