Задача 11

Еврооблигация погашается через 10 лет, доходность к погашению 10%, купон выплачивается раз в год в первые 3 года по ставке 10%, в следующие 4 года по ставке 8% и в оставшиеся 3 года по ставке 5% (см. рис. 1). Найти цену облигации.

Рис. 1

Решение. Основным правилом решения такого типа задач является принцип последнего купона, т.е. сначала по формуле 5 или 7 (проще 5, так как нет дробного купонного периода) находится цена облигации при купоне, равном дальнему (последнему), а затем к нему добавляются купонные разницы между ним и предыдущим, между предыдущим и предпредыдущим и т.д., пока не дойдем до первого купона. При этом число периодов (в формуле они являются степенями) для каждой такой разницы представляет собой число купонных периодов от даты нахождения цены (условно говоря, сегодня) до последнего периода, когда платится та ставка, для которой и рассчитывается данная купонная разница. Формализуем вышесказанное в виде формулы:

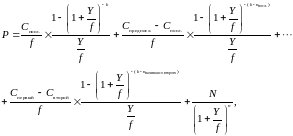(8)

где Р – цена инструмента, N – номинал, k – число купонных периодов от даты нахождения цены до погашения, С_посл., С_{предпосл.}, С_первый, С_второй – соответственно годовые ставки последнего, предпоследнего, первого и второго купонов в процентах от номинала, Y – доходность к погашению в долях единицы, f – частота выплаты купона в год, n_посл. число периодов с выплатой последнего купона, n_{начиная со второго} – число периодов с выплатой купонов начиная со второго (т.е. кроме периодов с первой ставкой). Подставим данные задачи 11 в формулу 8. Так как f  = 1, исключаем f из расчетов:

Задача 12

Еврооблигация погашается через 10 лет 1 месяц, доходность к погашению 10%, ежеквартальный купон выплачивается в последние 2 года по ставке 10% годовых, в предыдущие 4 года по ставке 7% и по ставке 5% до этого, то есть в первые 4 года 1 месяц (рис. 2). Найти цену облигации.

Решение. В отличие от предыдущей, в данной задаче есть дробный купонный период, так как купон ежеквартальный, а первый купон выплачивается через 1 месяц, поэтому необходимо будет брать за основу формулу 7. Преобразуем формулу 7 для облигации с различными фиксированными купонами. Принципы последнего купона и разности периодов остаются в силе.

(9)

Рис. 2

Все обозначения встречались и интерпретировались ранее в формулах 7 и 8.

Дробный период равен 1/3. НКД составит 5/4 (купон деленный на частоту выплаты в год), умноженное на 2 (число мес. с начала купонного периода) и деленное на 3 (число мес. в купонном периоде). Итого 5/4  2/3 = 0,833% от номинала. В нашем случае nпосл. = 8, так как включает в себя 2 года (см. рис. 2) по 4 периода (купон ежеквартальный), а nначиная со второго включает 6 лет (см. рис. 2) по 4 периода, то есть 24. Число полных периодов составляет 10 лет по 4 периода, т.е. k = 10  4 = 40. Подставим данные задачи в формулу 9:

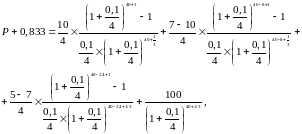
откуда P = 76,86.

Задача 12 (для самоконтроля)

Еврооблигация погашается через 12 лет и 9 месяцев, доходность к погашению 8%, полугодовой купон выплачивается в последние 3 года по ставке 3% годовых, в предыдущие 5 лет по ставке 4% и по ставке 6% до этого, т.е. в первые 4 года 9 месяцев (рис. 2). Найти цену облигации.

Обращаем внимание на то, что формулы 8 и 9 справедливы только в тех случаях, когда купонные ставки либо все время возрастают, либо все время убывают в течение срока жизни инструмента. Если же ставки то возрастают, то убывают, формулы 8 и 9 нуждаются в модификации. Однако такое на практике не встречается, поэтому эти случаи нами не рассматриваются.

Формулу цены облигации (например 4) можно также записать через процентные ставки спот на сроки до соответствующих купонов, так как доходность к погашению облигации есть среднее геометрическое¹ ставок спот на соответствующие сроки. Эти ставки спот формируют процентную кривую по любым инструментам (кредитам, облигациям, нотам и т.д.), которые обладают такими же кредитными качествами (рейтингом), как и сама облигация, выражаемая через ставки спот. Формулу цены облигации можно записать в следующем виде

(10)

где S₁, S₂, S_n – процентные ставки спот на сроки до соответствующих купонов.

Остальные обозначения были интерпретированы, когда приводилась формула 4. Так, например, если f = 4 и облигация погашается через 1,5 года, то S₁ будет спот-ставкой на 3 месяца, S₂ – на 6 месяцев, а S_n – на 1,5 года.