Обратная задача теории погрешностей и ее решение методом равных влияний

Обратная задача теории погрешностей состоит в том, чтобы определить с какой точностью необходимо задавать значения аргументов функции , чтобы ее погрешность не превосходила заданной величины  ? Эта задача математически неопределена, так как заданную погрешность можно обеспечить при любом наборе предельных абсолютных погрешностей аргументов удовлетворяющих условию:

Простейшее решение обратной задачи дает принцип равных влияний, согласно кото- рому вклады всех аргументов в формирование абсолютной погрешности функции равны:

Отсюда

, где

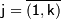
Иногда при решении обратной задачи по принципу равных влияний абсолютные погрешности отдельных аргументов оказываются настолько малыми, что вычислить или измерить эти величины с соответствующей точностью невозможно. В таком случае отступают от принципа равных влияний, чтобы увеличение погрешности одних переменных компенсировать уменьшением погрешности других.(Андреев-9)