Тема 6 Планирование погашения долга.

6.1 Способы погашения долга

Долг погашается либо единовременным платежом, либо в рассрочку, т.е. несколькими платежами.

Планирование погашения долга – это расчет будущих расходов, связанных с погашением долга.

При единовременном погашении планирование погашения долга – это расчет наращенной суммы и суммы процентов (темы 1 и 2).

При погашении в рассрочку планирование погашения долга - это расчет следующих показателей:

- срочные уплаты - это периодические расходы, связанные с погашением долга (они возникают, т.к. необходимо периодически погашать очередную часть долга и выплачивать проценты по остатку задолженности);

- обслуживание долга – это общие расходы, связанные с погашением долга (аналог наращенной суммы);

- стоимость долга - это разница между общими расходами и основным долгом (аналог суммы процентов).

6.2 Погашение долга равными долями.

В этом случае срочные уплаты – это доля долга, плюс проценты, начисленные на остаток задолженности. Т.к. остаток задолженности постоянно уменьшается, то, соответственно, проценты тоже уменьшаются, а значит, уменьшаются и срочные уплаты:

……………………………..

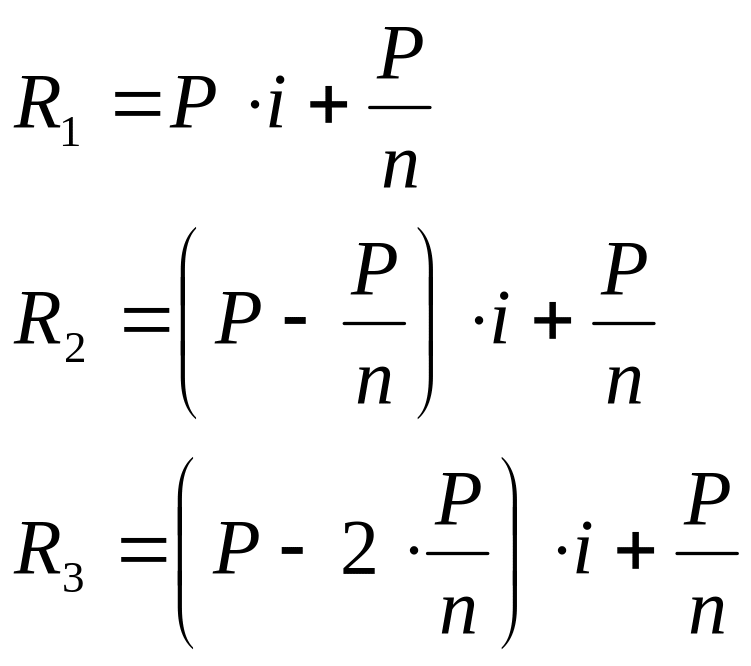
, где -срочные уплаты в период k (k=1,2,3….n),

Р – первоначальная сумма долга,

i - ставка процентов

n - срок долга.

Обслуживание и стоимость долга находят по формулам:

, где S - обслуживание долга,

I - стоимость долга.

6.3 Погашение долга равными срочными уплатами.

В этом случае срочные уплаты рассчитываются по формуле платежа постоянной обычной ренты (аннуитетный платеж):

Обслуживание и стоимость долга находят по формулам:

,

6.4 Потребительский кредит

Существует другой подход к погашению долга равными срочными уплатами, называемый потребительский кредит, когда сразу в момент выдачи кредита определяется его стоимость (сумма процентов), исходя из суммы первоначального долга:

Общ расходы

Затем общую сумму расходов делят по количеству выплат и находят срочные уплаты:

Этот способ является самым несправедливым, т.к. кредит погашается в рассрочку, но при этом проценты начисляются не на остаток задолженности, а на всю сумму долга, то есть получается, что заемщик платит проценты за кредит, которым не пользуется.

Так как ставка, указываемая при потребительском кредите, не отражает реальной доходности операции, то для расчета процентов за текущий период используется правило78, согласно которому для кредита сроком 1 год с ежемесячным погашением проценты за каждый месяц определяется по схеме:

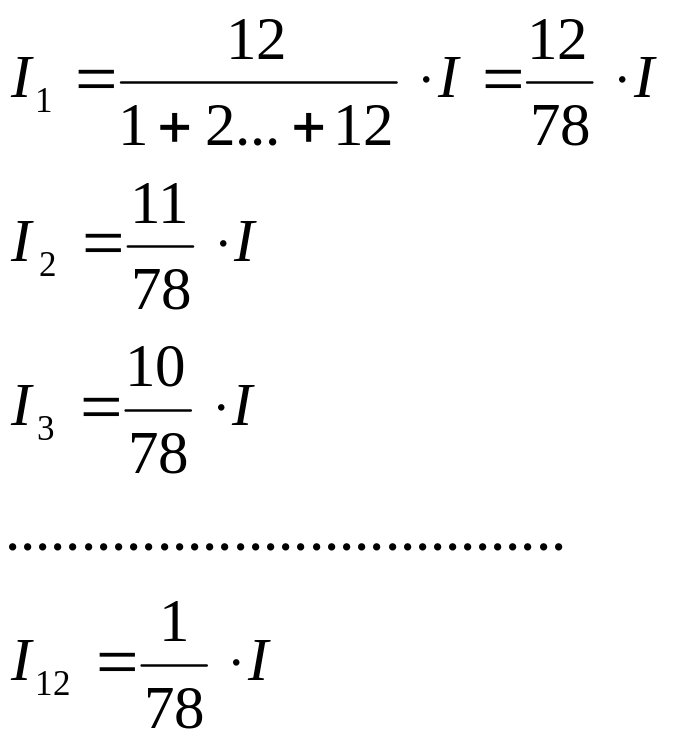
В общем случае эта схема записывается в виде:

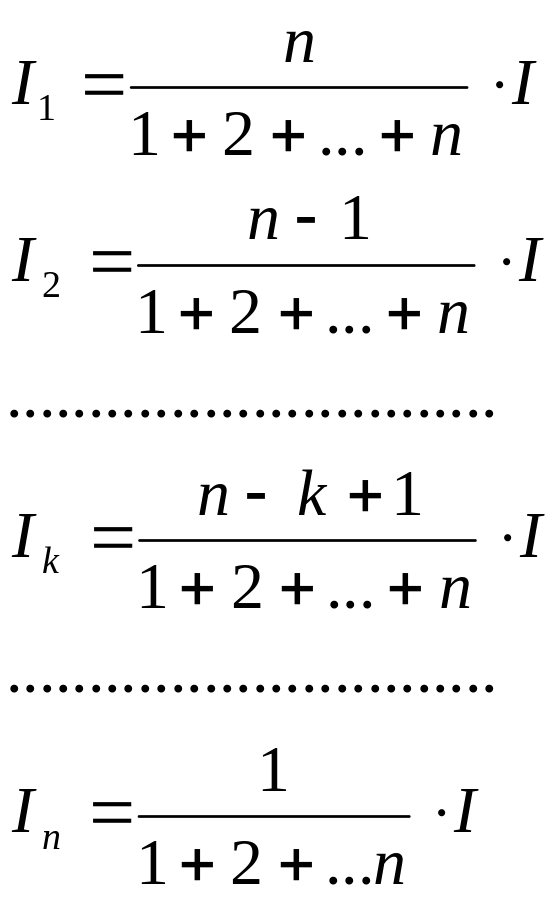
Если погашение долга осуществляется несколько раз в год, то во всех формулах делается следующая замена для срока и ставки: , , где m - количество выплат за год.

срочные уплаты - это периодические расходы, связанные с погашением долга (они возникают, т.к. необходимо периодически погашать очередную часть долга и выплачивать проценты по остатку задолженности)

обслуживание долга – это общие расходы, связанные с погашением долга

стоимость долга - это разница между общими расходами и основным долгом

план погашения – это таблица, в которой для каждого периода погашения указываются: остаток задолженности, проценты, погашение долга, срочные уплаты

погашение долга равными долями (равными суммами основного долга) - когда первоначальная сумма долга делится на равные доли по количеству выплат, при этом проценты начисляются на остаток задолженности, и выплачивается периодически вместе с долями

погашение долга равными срочными уплатами - когда основной долг и начисленные проценты выплачиваются постоянной обычной рентой

погашение долга единовременным платежом - когда первоначальная сумма долга погашается одним платежом в конце срока, при этом проценты начисляются на сумму основного долга и выплачиваются либо периодически (простые проценты), либо одним платежом вместе с долгом (сложные проценты)

потребительский кредит - частный случай погашения равными срочными уплатами, когда сразу в момент выдачи кредита определяется его стоимость (проценты), исходя из суммы первоначального долга, без учета будущих остатков задолженности.

7.1 Курс ценных бумаг

Наиболее распространенными ценными бумагами являются акции и облигации. Выпускаются эти ценные бумаги по номиналу, а покупаются и продаются по рыночной цене или курсу.

Курс ценной бумаги – это рыночная цена в расчете на 100 единиц номинала:

, где K - курс ценной бумаги;

P – рыночная цена;

N – номинал.

Курс очень удобен, так как позволяет сопоставить цену с номиналом:

а) K>100, значит цена больше номинала P>N ,

б) K=100, значит цена равна номиналу P=N ,

в) K<100, значит цена меньше номинала P<N .

7.2 Облигация, ее параметры и виды.

Облигация – это долговая ценная бумага, которая погашается в конце срока и дает право на получение процентов (купонов).

Параметры облигации:

- срок облигации – это интервал времени до погашения;

- номинал облигации – это сумма, которая будет выплачена в момент погашения;

- купонная ставка – это ставка, по которой начисляются проценты на номинал:

, где I – сумма процентов (купонов);

g – купонная ставка.

- количество выплат за год - согласно которому корректируется ставка и срок:

, , где m – количество выплат за год.

Виды облигаций:

1) облигации без выплаты процентов (бескупонные) - когда проценты не начисляются и не выплачиваются, в конце срока только погашается номинал, поэтому их цена всегда ниже номинала;

2) облигации с периодической выплатой процентов (купонные) - когда проценты периодически начисляются и выплачиваются, а в конце срока еще и погашается номинал; цена таких облигаций может быть выше и ниже номинала;

3) облигации с единовременной выплатой процентов в конце срока - когда проценты начисляются периодически, но выплачиваются одним платежом в конце срока вместе с погашением номинала (т.е. проценты периодически начисляются, но не выплачиваются, они накапливаются, в результате, сумма, которая будет выплачена в конце срока – это наращенная сумма сложных процентов); цена таких облигаций всегда выше номинала, так как включает проценты, накопленные от момента выпуска облигации.

7.3 Доходность облигаций

Доход по облигациям зависит от выплаты процентов и разницы между номиналом и ценой, поэтому купонная ставка не отражает реальную доходность операции.

Доходность облигации – это эквивалентная ставка простых либо сложных процентов, которая дает тот же результат, что и все будущие выплаты по облигации (т.е. все равно, вложить ли деньги в облигацию, или разместить на счет в банке под проценты по ставке, равной доходности):

,

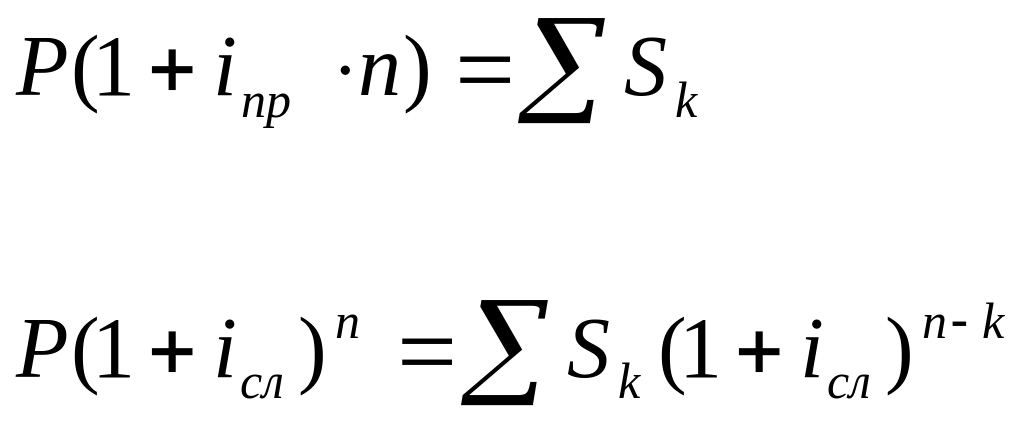где i – доходность облигации;

n – срок до погашения облигации;

P – цена облигации;

размер выплаты в срок k.

Для разных видов облигаций из этих уравнений выводят формулы доходности:

1) доходность облигаций без выплаты процентов:

2) доходность облигации с периодической выплатой процентов:

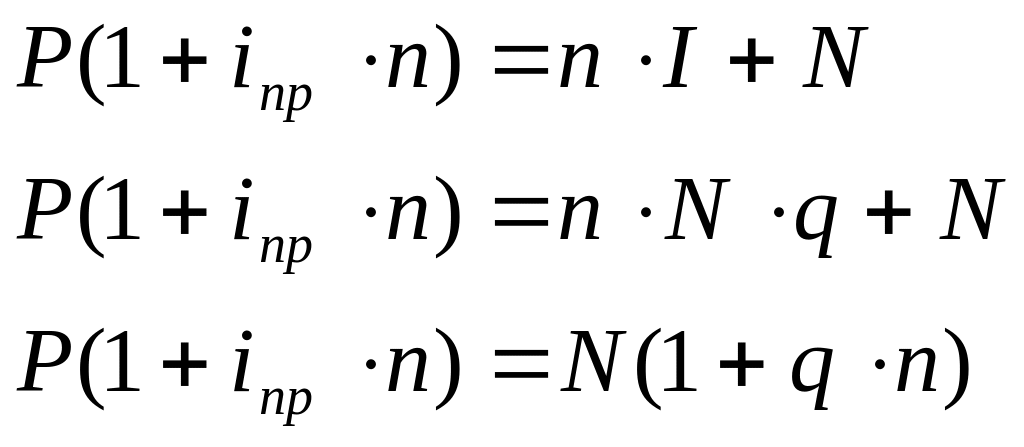
- получили уравнение степени n,

которое при n > 3 не разрешимо аналитически и решается приближенными методами на компьютере;

3) доходность облигаций с единовременной выплатой процентов.

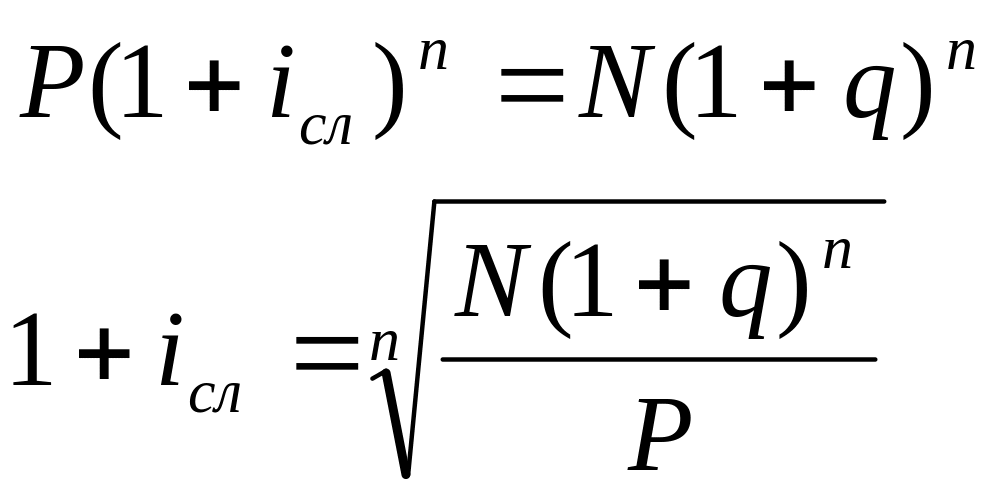
7.4 Оценка стоимости и риска облигации.

Оценка стоимости облигаций - это расчет цены, эквивалентной всем будущим выплатам, т.е. это расчет современной величины всех выплат по облигации (какой должна быть сейчас цена облигации, чтобы будущие выплаты соответствовали заданному уровню доходности):

, где

P – оценочная цена облигации;

i – доходность облигации;

- размер выплаты в срок k.

Чем выше выбранный уровень доходности, тем меньше должна стоить облигация, таким образом, оценочная стоимость облигации – это тот уровень цены, выше которой нет смысла покупать облигацию (т.к. ее доходность будет ниже заданной).

Если выплаты осуществляются несколько раз за год, то в формуле делается следующая замена: , , где m – количество выплат за год.

Риск облигации сопоставим с ее сроком - чем больше срок, тем больше риск.

Если облигации имеют одинаковый срок, то их риск зависит от «профиля» облигации, то есть от распределения выплат во времени.

Очевидно, что наиболее рискованной является облигация, у которой основная часть выплат приходится на конец срока, менее рискованной является облигация, где основная часть выплат приходится на начало срока.

Риск облигаций с одинаковым сроком оценивается с помощью среднего срока выплат.

Дюрация – это средний срок выплат, рассчитывается по формуле средней арифметической взвешенной 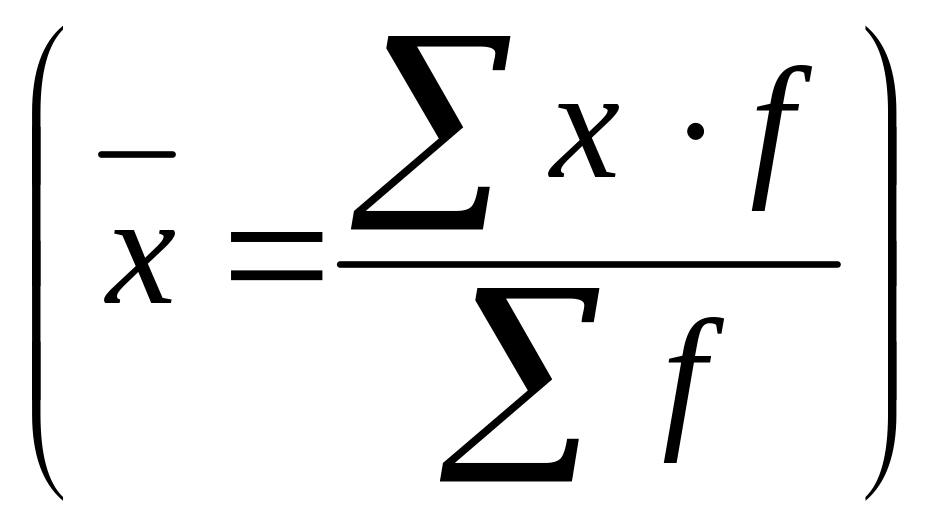, где весом является размер выплаты, дисконтированной на начало операции:

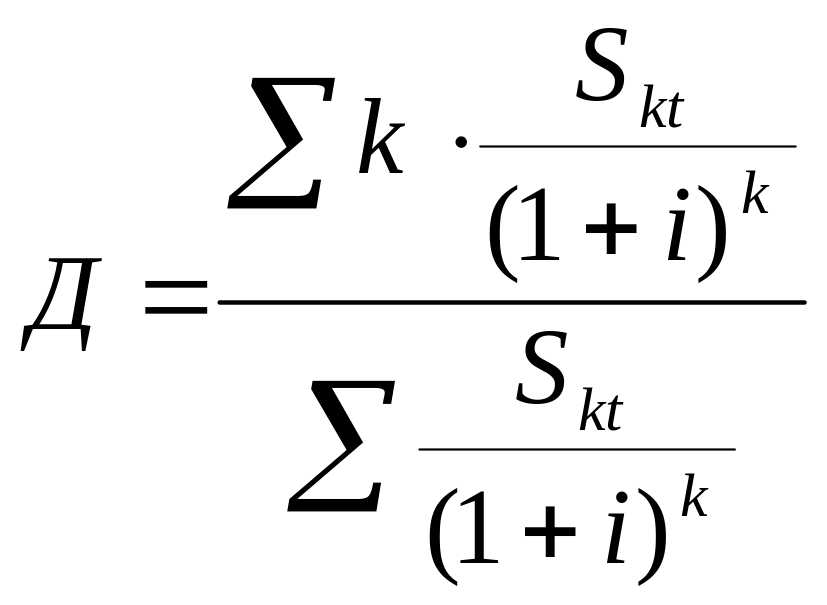, где Д – дюрация (средний срок выплат).

В знаменателе формулы дюрации стоит цена облигации:

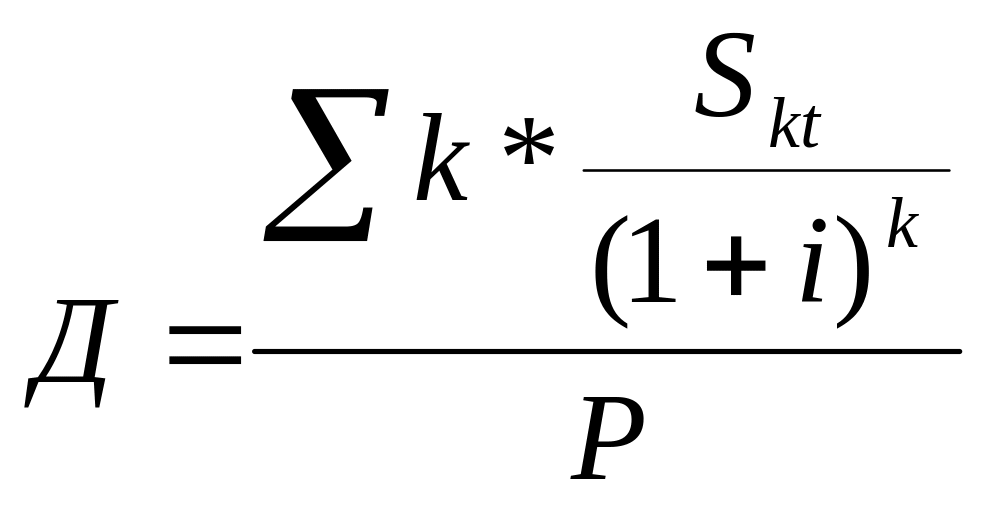
7.5 Оценка и доходность акций.

Акция, в отличие от облигации, не имеет срока погашения, следовательно, единственным источником дохода являются дивиденды.

Выплата дивидендов представляет собой вечную ренту, поэтому для оценки стоимости акций применяют формулу современной величины постоянной обычной ренты :

,

где Р – цена акции;

– текущая доходность акции;

I – сумма дивидендов, которая определяется исходя из номинала акции и ставки дивиденда:

, где g – ставка дивидендов.

Из формулы цены получают формулу для текущей доходности акций:

Так как акция не погашается, то, как правило, ее покупают для того, чтобы через некоторое время продать. В этих случаях доходность акции находится в виде эквивалентной простой ставки и называется полной доходностью акций:

,

где Р цена покупки акции,

Q – цена продажи акции.

7.6 Оценка портфеля ценных бумаг

Как правило, каждый банк содержит несколько видов акций , облигаций и других видов ценных бумаг, так называемый портфель ценных бумаг.

Оценка портфеля – это расчет следующих показателей:

1) оценка стоимости портфеля – это оценочная стоимость всех ценных бумаг:

,

где P– стоимость портфеля; - цена ценных бумаг вида j; - количество ценных бумаг вида j;

2) доходность портфеля – средняя арифметическая взвешенная из доходностей всех ценных бумаг, где весом является количество ценных бумаг: ,

где i – доходность портфеля; - доходность ценных бумаг вида j;

3) дюрация портфеля – средняя арифметическая взвешенная из дюраций всех ценных бумаг портфеля ,

где Д – дюрация портфеля; - дюрация ценных бумаг вида j.

доходность облигации – это эквивалентная ставка простых либо сложных процентов, которая дает тот же результат, что и все будущие выплаты по облигации

дюрация – это средний срок выплат, рассчитывается по формуле средней арифметической взвешенной, где весом является размер выплаты, дисконтированной на начало операции

купонная ставка – это ставка, по которой начисляются проценты на номинал

курс ценной бумаги – это рыночная цена в расчете на 100 единиц номинала

номинал облигации – это сумма, которая будет выплачена в момент погашения

облигации без выплаты процентов (бескупонные) - когда проценты не начисляются и не выплачиваются, в конце срока только погашается номинал, поэтому их цена всегда ниже номинала

облигации с единовременной выплатой процентов в конце срока - когда проценты начисляются периодически, но выплачиваются одним платежом в конце срока вместе с погашением номинала (т.е. проценты периодически начисляются, но не выплачиваются, они накапливаются, в результате, сумма, которая будет выплачена в конце срока – это наращенная сумма сложных процентов); цена таких облигаций всегда выше номинала, так как включает проценты, накопленные за срок от момента выпуска облигации

облигации с периодической выплатой процентов (купонные) - когда проценты периодически начисляются и выплачиваются, а в конце срока еще и погашается номинал; цена таких облигаций может быть выше и ниже номинала

облигация – это долговая ценная бумага, которая погашается в конце срока и дает право на получение процентов (купонов)

оценка стоимости облигаций - это расчет цены, эквивалентной всем будущим выплатам, т.е. это расчет современной величины всех выплат по облигации

срок облигации – это интервал времени до погашения