Тема 4. Учет инфляции в финансово-экономических

расчетах.

4.1 Сущность инфляция и ее параметры.

Инфляция – это снижение покупательной способности денег (т.е. рост цен).

Параметры инфляции:

уровень инфляции – показывает, насколько процентов выросли цены; задается за период времени (месяц, квартал, полугодие, год);

индекс (темп) инфляции – показывает, во сколько раз выросли цены; находится за любой срок по формуле:

, где - индекс инфляции за срок,

- уровень инфляции за период,

N - количество периодов за срок.

Индекс инфляции используется для:

1) индексации денежной суммы, когда исходную сумму умножают на индекс инфляции:

, где исходная сумма,

сумма с учетом инфляции;

2) определения реальной покупательной способности денежной суммы, когда исходную сумму делят на индекс инфляции:

, где реальная покупательная способность денежной суммы.

4.2 Учет инфляции при начислении процентов

В банках при начислении процентов инфляцию учитывают двумя способами:

1) индексация первоначальной суммы, когда первоначальная сумма долга периодически индексируется согласно заранее оговоренному индексу:

2) индексация процентной ставки, когда наращение осуществляется, по так называемой брутто-ставке, которая учитывает реальную доходность операции и инфляционную премию:

,

где - наращенная сумма с учетом инфляции,

Р - первоначальная сумма долга,

n - срок долга,

- индекс инфляции за срок долга,

i - нетто-ставка, т.е. реальная доходность операции,

- брутто-ставка.

Значение брутто-ставки определяют из уравнения эквивалентности Фишера, в котором приравнивают результаты учета инфляции:

а) брутто-ставка простых процентов: б) брутто-ставка сложных процентов:

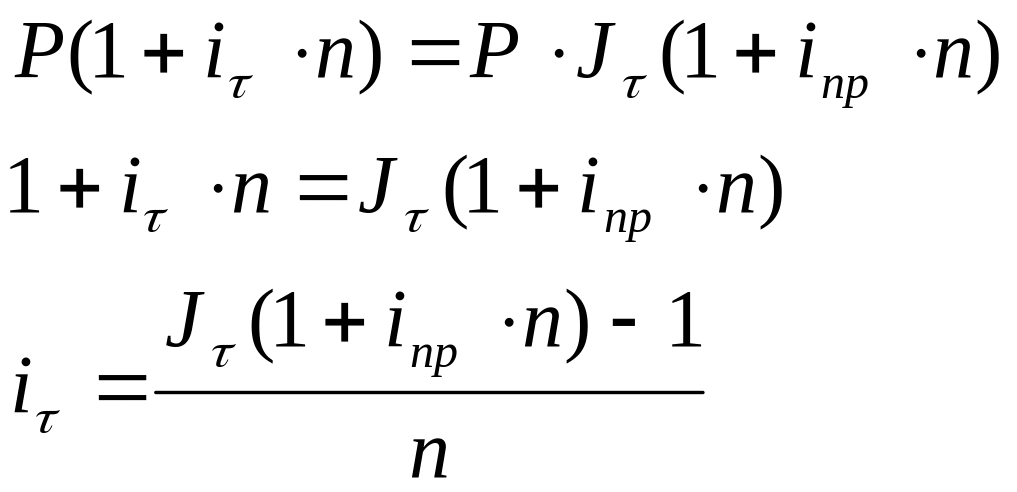
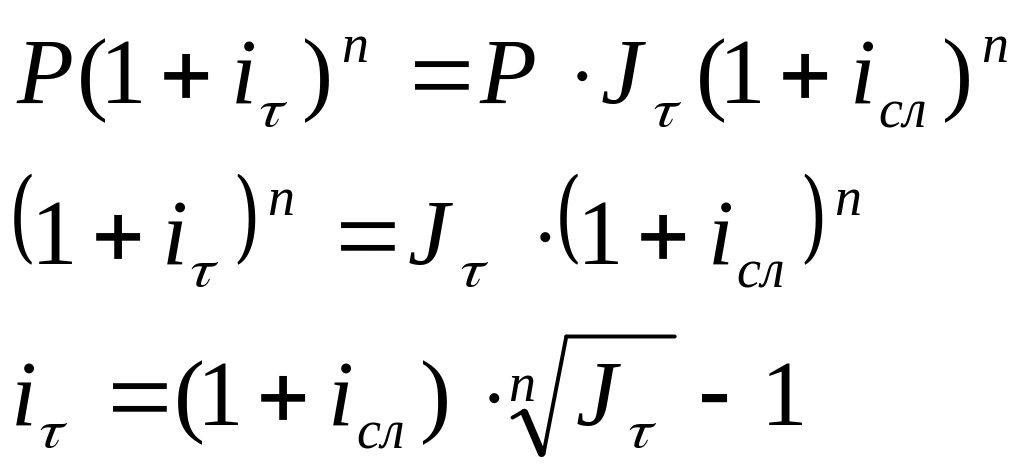
индекс инфляции – показывает, во сколько раз выросли цены, рассчитывается за любой срок

индексация денежной суммы - умножение исходной суммы на индекс инфляции

индексация первоначальной суммы – когда начисление процентов происходит при условии, что первоначальная сумма долга периодически индексируется согласно заранее оговоренному индексу

индексация процентной ставки - когда начисление процентов осуществляется, по так называемой брутто-ставке, которая учитывает реальную доходность операции и инфляционную премию

инфляция – это снижение покупательной способности денег (т.е. рост цен)

реальная покупательная способность денежной суммы - деление исходной суммы на индекс инфляции

уравнение Фишера – это уравнение эквивалентности, в котором приравнивают результаты начисления процентов по нетто- и брутто-ставкам

уровень инфляции – показывает, насколько процентов выросли цены, задается за период времени (месяц, квартал, полугодие, год)

Тема 5. Потоки платежей. Финансовые ренты.

5. 1 Финансовая рента

Поток платежей – это последовательность платежей в разные моменты времени по операциям, связанным с начислением процентов.

Например, потоком являются поступления (положительные платежи) и выплаты (отрицательные платежи) по вкладам до востребования.

Финансовая рента (аннуитет) – это поток положительных периодичных платежей

Например, рентой являются: взносы в пенсионный и страховой фонды, погасительные платежи потребительского кредита, выплата процентов по облигациям.

Параметры финансовой ренты:

- член ренты - размер платежа;

- период ренты – интервал времени между соседними платежами;

- срок ренты – интервал времени от начала первого до конца последнего периода;

- ставка ренты – ставка, по которой начисляются проценты.

Виды финансовой ренты:

- постоянная рента, если платежи одинаковы, и переменная рента, если платежи различны;

- обычная рента (постнумерандо), если платеж делается в конце периода, и рента

пренумерандо, если платежи делаются в начале периода;

- годовая рента, если один платеж в год, и срочная рента, если несколько платежей за год;

- конечная рента, если ее срок ограничен, и вечная рента, если ее срок не ограничен.

5.2 Обычная рента и ее обобщающие показатели

Обобщающие характеристики финансовой ренты:

- наращенная сумма ренты S – это сумма всех платежей вместе с процентами, начисленными на конец ренты;

- современная величина ренты P – это сумма всех платежей, дисконтированных на начало ренты.

Наращенная сумма ренты определяется, когда необходимо узнать общий результат накопления в будущем. Современная величина определяется, когда необходимо узнать первоначальную или текущую задолженность на данный момент времени.

Наиболее распространенной является обычная рента:

S =

Если рента является постоянной, т.е. , то данные формулы представляют собой суммы членов геометрических прогрессий:

где S - наращенная сумма ренты

P - современная величина ренты

R - платеж ренты

i - ставка ренты

n - срок ренты

- коэффициент наращения ренты, показывает во сколько раз наращенная сумма S больше платежа R;

-коэффициент приведения ренты, показывает во сколько раз современная величина Р больше платежа R.

Из формул наращенной суммы S и современной величины P получают формулы для расчета платежа ренты:

5.3 Финансовые ренты пренумерандо

Р

S

0

1

2

3

n

n-1

…

Если сравнить эти формулы с обычной рентой, то можно увидеть следующую взаимосвязь:

наращенная сумма ренты пренумерандо,

- наращенная сумма обычной ренты,

- современная величина ренты пренумерандо,

Р - современная величина обычной ренты.

5.4 Вечные финансовые ренты

Определить наращенную сумму вечной ренты невозможно, т.к. не задан срок, на который будут начислены проценты.

Современная величина вечной ренты определяется как предел современной величины постоянной обычной ренты при бесконечно большом сроке:

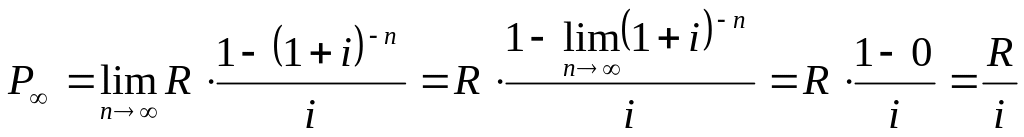
, где Р∞ - современная величина вечной ренты,

R - платеж ренты,

i - ставка ренты.

Из формулы современной величины выводят формулы для параметров вечной ренты:

- платеж вечной ренты:

- ставка вечной ренты:

вечная рента - если ее срок не ограничен

годовая рента - если один платеж в год

конечная рента - если ее срок ограничен

наращенная сумма ренты – это сумма всех платежей вместе с процентами, начисленными на конец ренты

обычная рента - если платеж делается в конце периода

переменная рента - если платежи различны

постоянная рента - если платежи одинаковы

поток платежей – это последовательность платежей в разные моменты времени по операциям, связанным с начислением процентов

рента пренумерандо - если платежи делаются в начале периода

современная величина ренты – это сумма всех платежей, дисконтированных на начало ренты

срочная рента - если несколько платежей за год (каждый месяц, квартал, полугодие либо год)

финансовая рента (аннуитет) – это поток положительных периодических платежей