Тема 3 Эквивалентность процентных ставок.

Финансовая эквивалентность платежей.

3.1 Эквивалентность процентных ставок.

Эквивалентные ставки - это ставки разного вида, которые в однотипных операциях приводят к одинаковым результатам.

Например, простая ставка 22% годовых будет эквивалентна сложной ставке 20% годовых для кредита 10 000 рублей сроком 2 года, т.к. в каждом случае сумма погашения кредита будет одинакова:

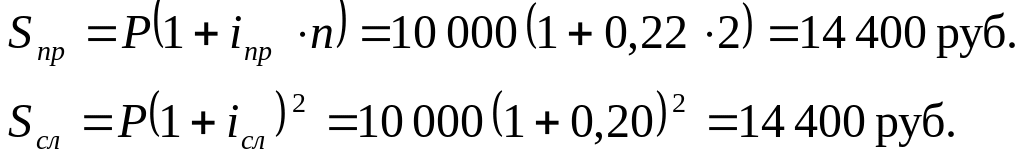
Замена в договоре одной ставки на эквивалентную ей ставку другого вида не меняет результатов операции.

В качестве результата операции удобно брать наращенную сумму, множитель наращения или проценты.

Формулы для эквивалентных ставок получают из уравнения эквивалентности, в котором приравниваются результаты операций:

1) эквивалентность простой и сложной ставок:

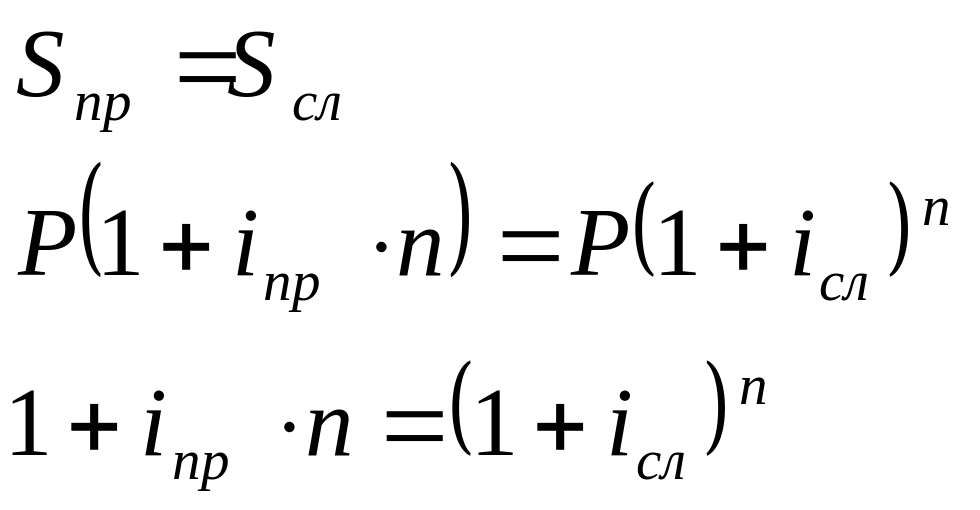
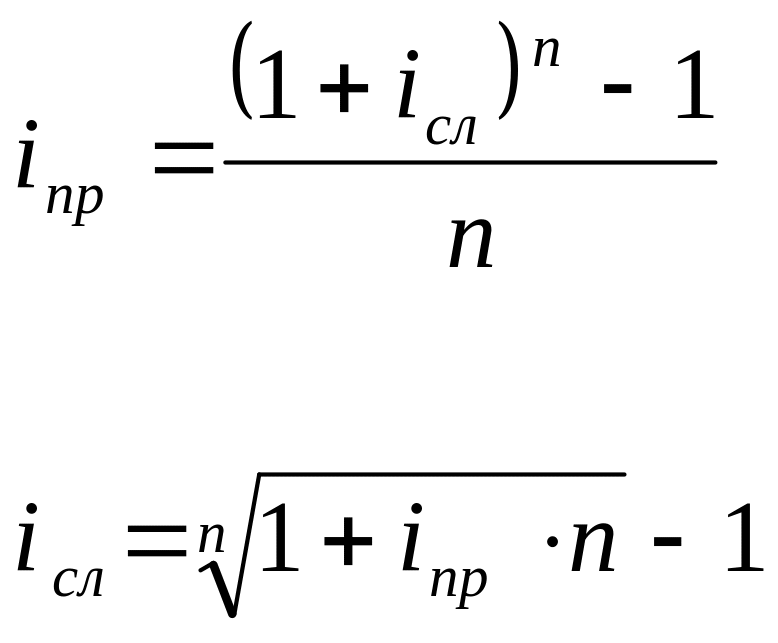
эквивалентность годовой сложной и номинальной ставок:

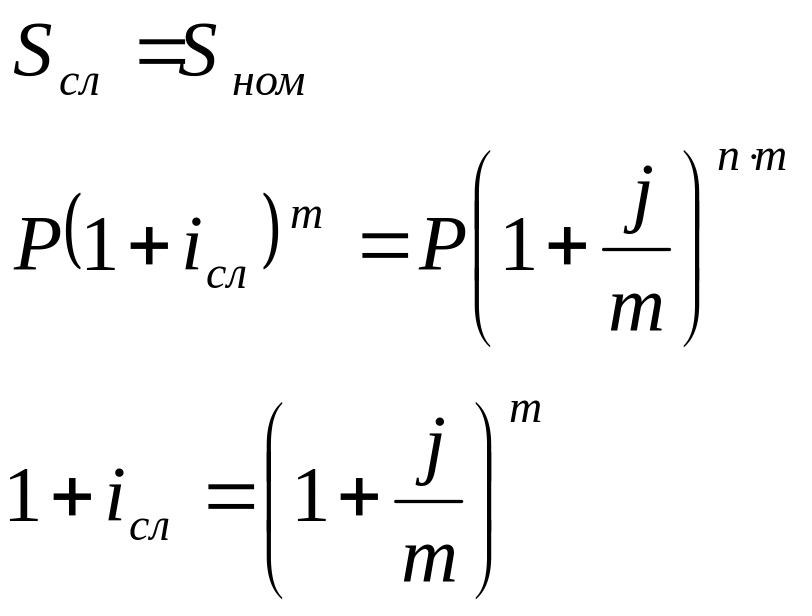
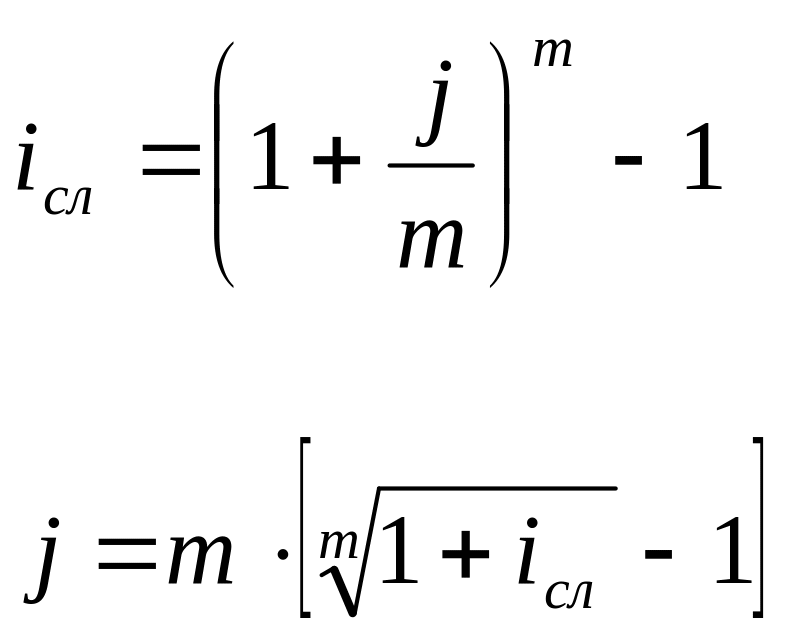
3) эквивалентность простой и учетной ставок:

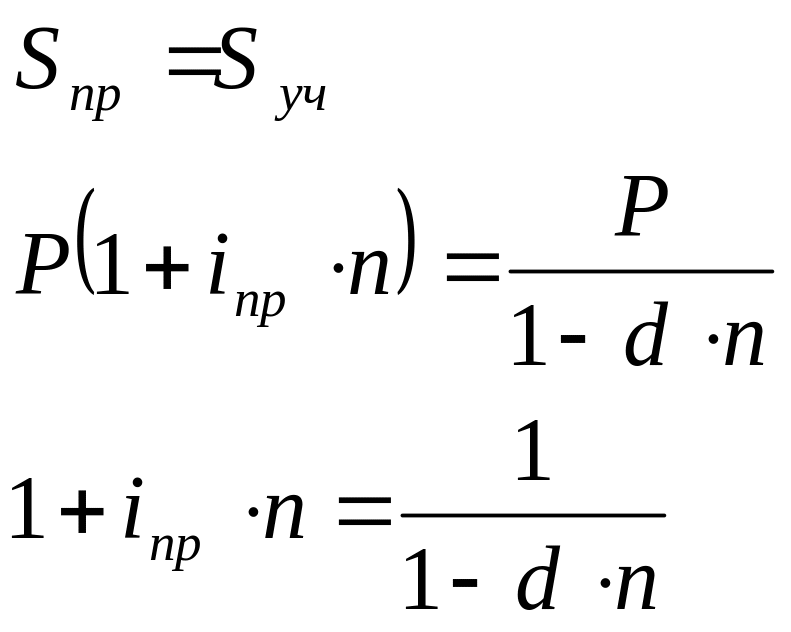
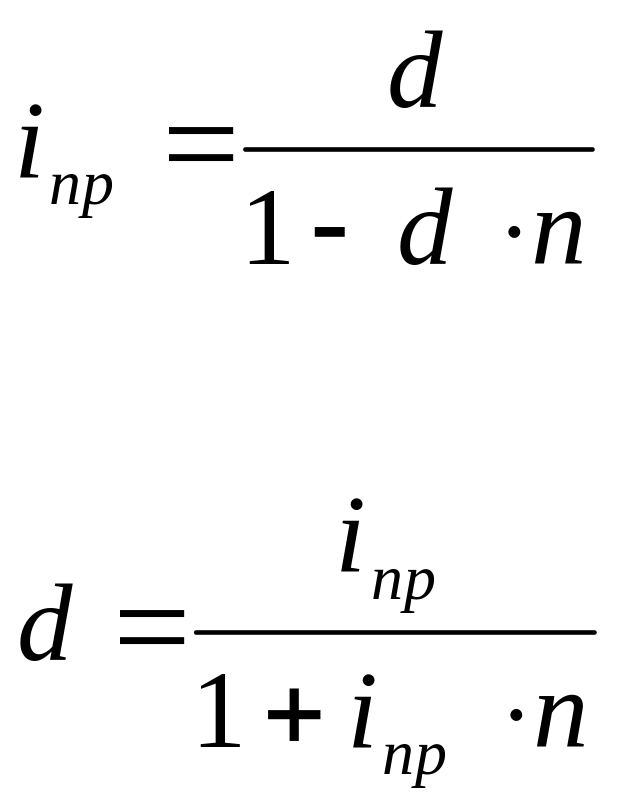
Если выстроить эквивалентные ставки в порядке возрастания, то получим:

Эквивалентные ставки простых и сложных процентов называют – доходностью операции.

Доходность – это ставка, которая принесет тот же доход (результат операции), поэтому сравнивают операции по уровню их доходности.

3.2 Доходность нескольких однотипных операций.

Доходность нескольких однотипных операций находят с помощью средней ставки.

Средняя ставка- это эквивалентная ставка простых процентов, которая приводит к тому же результату, что и фактические ставки операций.

сумма простых процентов:

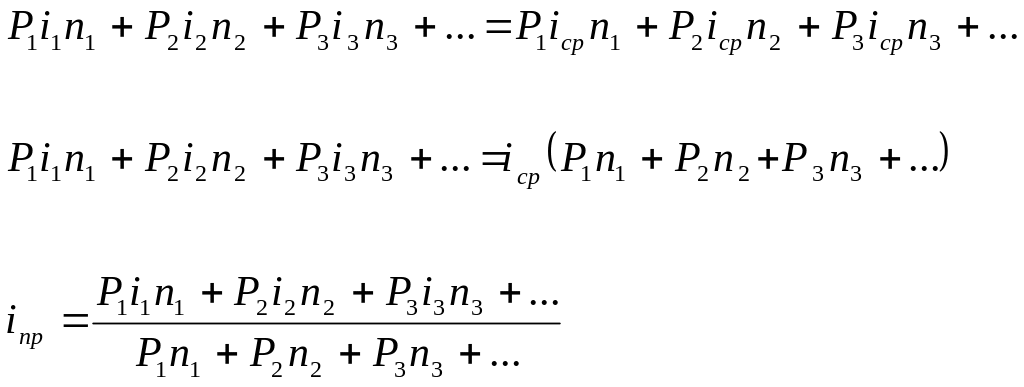
, где iср - средняя ставка

i1 ,i2 … - фактические ставки

n1 ,n2 …- сроки операций

P1 , P2 …- первоначальные суммы операций

3.3 Финансовая эквивалентность платежей.

Эквивалентные платежи – это платежи, которые будут равны, если их привести к одному и тому же сроку по одной и той же процентной ставке.

Чтобы привести платеж к более позднему сроку, необходимо начислить проценты на платеж: , где R - исходный платеж,

S - приведенный платеж,

n - срок до приведения.

Чтобы привести платеж к более раннему сроку необходимо дисконтировать платеж (т.е. удержать проценты):

Приведение платежей используется в ситуациях, когда необходимо:

- изменить сроки платежей;

- поменять количество платежей;

- объединить несколько платежей в один – консолидация платежей.

В этих случаях, чтобы ни одна из сторон не понесла убытки, руководствуются принципом финансовой эквивалентности платежей, когда все платежи приводятся к одному сроку и приравниваются результаты по старым и новым условиям:

S1 + S2 +…. + SK = S1* + S2* +…. + SN*

где S – размер приведенного платежа по старым условиям,

S*- размер приведенного платежа по новым условиям,

К - количество старых платежей,

N - количество новых платежей.

В случае объединения платежей, все платежи приводят к сроку нового консолидированного платежа, и, поэтому, принципы финансовой эквивалентности преобразовывается к виду: , где -консолидированный платеж.

доходность операции - эквивалентная ставка простых и сложных процентов (эффективность операции)

принцип финансовой эквивалентности платежей - когда все платежи приводятся к одному сроку и приравниваются результаты по старым и новым условиям

средняя ставка- это эквивалентная ставка простых процентов, которая приводит к тому же результату, что и фактические ставки по рассматриваемым операциям

уравнения эквивалентности ставок – уравнение, в котором приравниваются результаты операций

чтобы привести платеж к более позднему сроку необходимо начислить проценты на платеж

чтобы привести платеж к более раннему сроку необходимо дисконтировать платеж (т.е. удержать проценты)

эквивалентные платежи – это платежи, которые будут равны, если их привести к одному и тому же сроку по одной и той же процентной ставке

эквивалентные ставки - это ставки разного вида, которые в однотипных операциях приводят к одинаковым результатам