Модификация уравнений массопередачи.

Локальная форма.

Процесс массопередачи, движущей силой в котором являлась разница химических потенциалов компонента в ядрах различных фаз, описывается следующим уравнением:

Расчет химических потенциалов представляет собой достаточно сложную задачу. В связи с этим на практике обычно пользуются уравнениями массоотдачи и массопередачи, содержащими в качестве движущей силы разность рабочей и равновесной концентраций компонента в одной из фаз:

Интегральная форма

Проинтегрировав предыдущее уравнение по величине межфазной поверхности всего аппарата или его участка и считая постоянными K_y, K_x = const на рассматриваемом участке, можно получить уравнения массопередачи в интегральной форме:

где

где y_в и y_н - движущие силы массопередачи в верхнем и нижнем сечениях аппарата (участка аппарата). Если в пределах интегрирования коэффициент распределения m = const или линию равновесия можно аппроксимировать прямой, средняя движущая сила определяется средней логарифмической величиной.

Объемные коэффициенты массоотдачи и массопередачи

При использовании интегральной формы уравнений массоотдачи и массопередачи проблемой является определение поверхности контакта фаз в реальном аппарате, так как она может складываться из поверхности струй, капель, пузырей, пены. В этом случае применяют модифицированные уравнения не содержащие величину межфазной поверхности.

Используется понятие удельной поверхности контакта фаз а как поверхности контакта, образующейся в единичном рабочем объеме аппарата:

м²/м³ .

Выразив F=a V, перепишем уравнения массоотдачи и массопередачи в виде

(*)

Коэффициенты массопередачи и массоотдачи с индексами “v” называются объемными.

Число и высота единиц переноса

Для наиболее распространенного типа массообменных аппаратов (цилиндрические вертикальные колонны) основным размером, зависящим от скорости массопередачи, является высота H.

Если площадь поперечного сечения аппарата S постоянна, то его объем можно записать

Подставив в уравнение (*) V, и используя интегральную форму уравнения материального баланса и решив его относительно H, получим

Первые сомножители этих уравнений называются высотой единиц переноса (ВЕП), а вторые - числом единиц переноса (ЧЕП).

Число единиц переноса - это изменение рабочей концентрации фазы на участке аппарата, отнесенное к средней по данному участку движущей силе процесса. Высота единиц переноса соответствует высоте участка аппарата, эквивалентного одной единице переноса.

Упрощенные модели массотдачи.

Выражение для локального коэффициента массоотдачи в двухкомпонентных смесях имеет вид

Его использование предполагает знание характера изменения коэффициента турбулентной диффузии D_т(y) и относительного диффузионного потока j_i*(y) в пограничном слое. Для массоотдачи через свободную (подвижную) поверхность контакта фаз в системах газ - жидкость, жидкость – жидкость модели для нахождения D_т(y) не существует, а определение j_i* требует совместного решения уравнений движения, неразрывности и конвективной диффузии, что зачастую не возможно. В этой связи для определения коэффициента массотдачи пользуются упрощенными моделями.

Пленочная модель (Нернст, Льюис, Уитмен). Предполагается, что вблизи межфазной поверхности располагается тонкая неподвижная или ламинарно движущаяся пленка толщиной _э, в которой сосредо­точено все сопротивление массоотдачи.

Параметром модели - эффективная толщина пленки _э. Модель является упрощенной и пригодна в основном лишь для качественного анализа.

Модель турбулентного диффузионного пограничного слоя Ландау – Левича.

М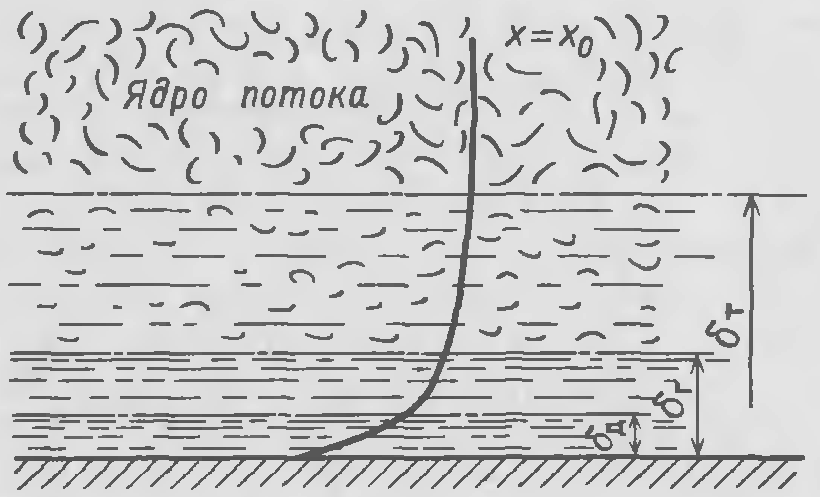 одель применима при больших значениях диффузионного критерия Прандтля, характерного для большинства жидкостей (Рr_g10³). Концентрация в ядре потока постоянна, медленно снижается в турбулентном пограничном слое (преобладают турбулентные пульсации), в вязком подслое скорость концентрация снижается заметно быстрее (возрастает молекулярная диффузия) и внутри тонкого диффузионного подслоя _д примыкающего к границе раздела фаз преобладает молекулярный перенос. В этом случае считают, что все сопротивление массоотдачи сосредоточено в вязком подслое толщиной _д.

,

Данная модель применима для количественного описания массоотдачи в жидкой фазе.

Модель проницания (Хигби). Массоотдача происходит во время контакта с поверхностью раздела фаз быстро сменяющих друг друга элементов жидкости (или газа) переносимых из ядра к границе раздела турбулентными пульсациями. При этом свежие элементы смывают уже прореагировавшие, и соответственно, массоотдача происходит при систематическом обновлении поверхности раздела фаз.

(*)

t_k – время контакта.

Модель обновления поверхности (Данквертс, Кишиневский). Как и в модели проницания, предполагается нестационарный массоперенос к неподвижному относительно границы раздела фаз слою. Однако допускается, что отдельные элементы приграничного слоя периодически замещаются другими, подводимыми за счет турбулентных пульсаций из ядра фазы, причем время контакта элементов с поверхностью может быть различным. Коэффициент массоотдачи может рассчитываться по (*), в котором величина t_к заменяется на t_cp - среднее время контакта элемента слоя с межфазной поверхностью.