Тема 6 моделирование флаттера в аэродинамической трубе

Исследования явления флаттера проводят в аэродинамических трубах (АДТ) с помощью моделей уменьшенного масштаба. При выполнении определенных критериев подобия между натурной конструкцией самолета и его уменьшенной моделью удается с требуемой точностью при меньших затратах времени и средств, без всякой угрозы для безопасности экипажа (которая существует при испытаниях натурной конструкции) исследовать такие опасные явления аэроупругости, как флаттер, дивергенция, реверс элеронов и др. Кроме того, простые модели позволяют выявить суть явления, отделить важные факторы от второстепенных, провести параметрические исследования, определить пути совершенствования конструкции, установить границы безопасных режимов полета. Моделирование флаттера в АДТ основывается на подходах, которые применяют для построения кинематически подобных систем.

Кинематически подобные системы сохраняют геометрическое подобие друг другу не только в статическом положении, но и в течение всего времени их движения. Для реализации подобия этих движений необходимо знать, каким именно требованиям должны удовлетворять такие системы. Данная задача была решена Ньютоном.

Решение оказалось прямым следствием второго закона Ньютона.

По второму закону Ньютона для систем 1 и 2 имеем:

Подобие движений будет обеспечено, если ускорения систем всегда будут оставаться пропорциональными. Тогда:

и, следовательно, в масштабных коэффициентах , где

K_F - масштаб сил,

K_m - масштаб масс,

K_a - масштаб ускорений.

Выразив масштабы ускорений через масштабы времени и линейных размеров, формулу можно записать в окончательном виде:

, где

K_t - масштаб времени,

K_L масштаб линейных размеров, обеспечивающий геометрическое подобие при движении обеих систем в соответствующие моменты времени.

Системы, параметры которых удовлетворяют формуле Ньютона, будут совершать кинематически подобные движения.

Следует особо подчеркнуть, что уравнение связывает четыре величины. Поэтому любые три из них могут быть заданы произвольно, а оставшаяся четвертая величина однозначно должна быть определена по формуле Ньютона. Последнее обстоятельство и является тем требованием, выполнение которого обеспечивает кинематическое подобие движения рассматриваемых систем.

1. Вопросы подобия

Для исследования в аэродинамических трубах малых скоростей флаттера самолетов с крыльями большого удлинения применяют отсечно-балочную модель. В моделях этой схемы (рис. 1) жесткостные характеристики крыла, фюзеляжа, оперения моделируются балками-лонжеронами переменного сечения (рис. 2), расположенными по осям жесткости.

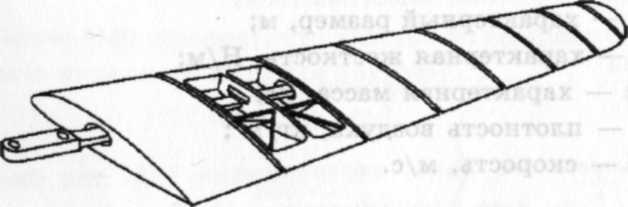
Рисунок 1. Отсечно-балочная модель крыла

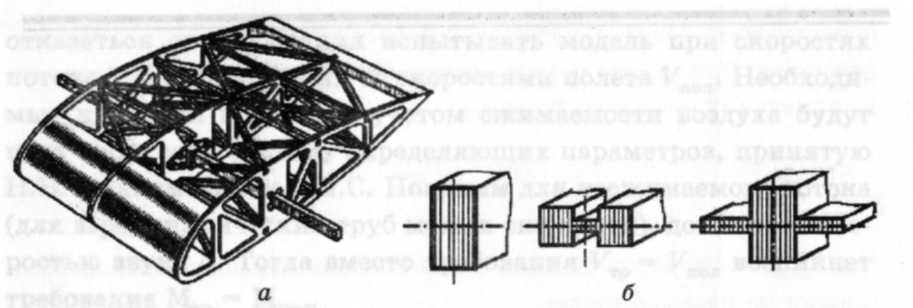
Рисунок 2. Основные элементы моделей: а) отсек; б) лонжероны с различной формой сечений

Аэродинамические обводы воспроизводят жесткими, отделенными друг от друга щелями, отсеками, закрепленными на балках-лонжеронах так, чтобы не стеснять их деформаций при колебаниях модели. На лонжероны и отсеки закрепляют доводочные грузы, обеспечивающие подобие модели по массово-инерционным характеристикам. Отсеки передают на лонжероны аэродинамические нагрузки.

Модели этой схемы успешно применяют в трубах малых скоростей для исследования флаттера самолетов, имеющих несущие и управляющие поверхности большого и умеренного удлинения.

Следует отметить, что модели отсечно-балочной схемы малопригодны для моделирования флаттера ЛА с несущими и управляющими поверхностями малого удлинения, когда на модели невозможно воспроизвести упругие характеристики натуры балкой. Такие модели также не следует использовать при числах М>0,6-0,7, потому что на стыках между отсеками модели могут возникать местные скачки уплотнения, тогда как в натурных условиях скачки такого типа возникать не будут.