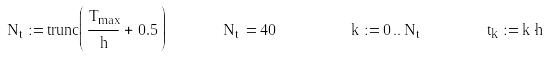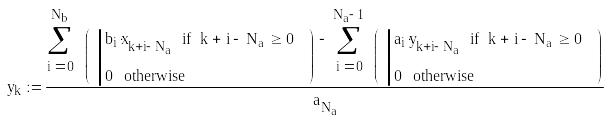Теоретичні засади
Нехай для певної неперервної передатної функції W(s) шляхом аналітичних перетворень отримано дискретну передатну функцію W(z):
для n m з
умови фізичної реалізації.
З дискретної передатної функції для моменту часу ti отримуємо
;
після чого ділимо почленно на найбільший степінь змінної – zn
.
Враховуючи теорему зміщення для
Z-перетворення
отримуємо
,
звідки знаходимо остаточний вираз для вихідної координати
.
Наприклад: 
.
Для моменту часу ti отримуємо
,
далі почленно ділимо на z2:
;
звідки
.
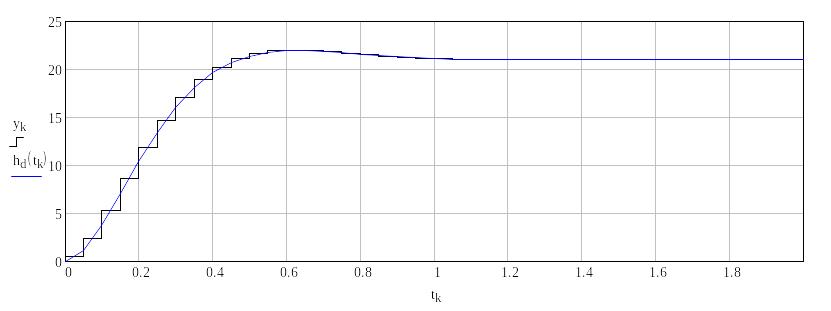
Таким чином, процес знаходження відгуку системи на вхідний сигнал (у нашому випадку – одиничний стрибкоподібний, тоді відгук системи є її перехідною функцією) у середовищі MathCAD може виглядати, як показано нижче.
MathCAD
Для перехідної характеристики завдання є одиничним xk : = 1 Початкові умови є нульовими yk : = 0
|
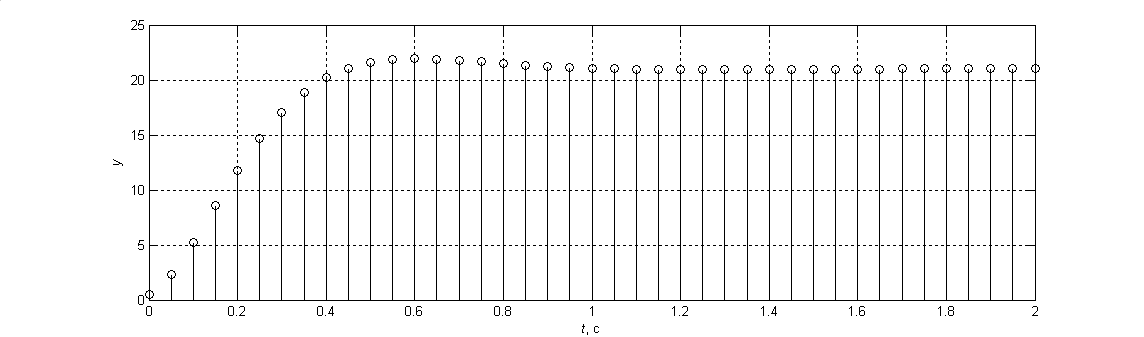
MATLAB
step(W), grid % побудова перехідної характеристики |
Перевірити перехідну характеристику отриманої замкненої дискретної системи також можна в середовищі MATLAB + Simulink, як це показано нижче. Зручність того чи іншого способу вирішується в кожному випадку окремо залежно від уподобань і знань дослідника.
|
|
Зменшивши на порядок крок дискретизації, перевірити вплив точності задавання коефіцієнтів дискретної передатної функції (кількість значущих цифр) на правильність відтворення перехідної характеристики. Зробити висновки стосовно необхідної розрядності обчислювального пристрою в обох випадках. |