Біноміальна форма
 ;
; ;
;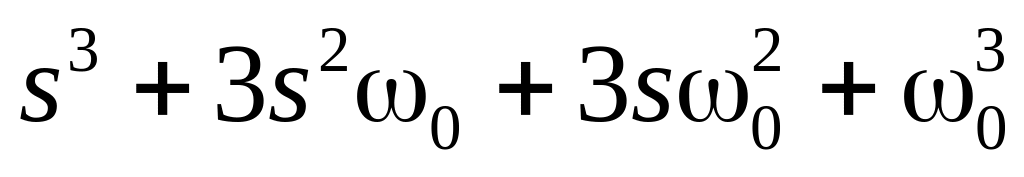 ;
;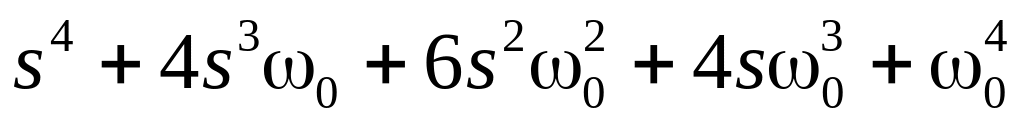 ;
; ;
;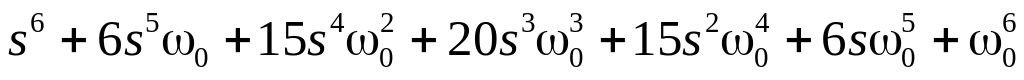 ;
;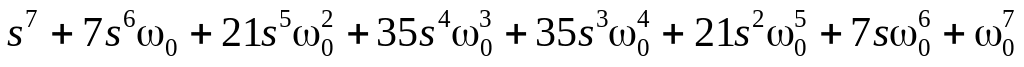 .
.
Форма Баттерворта
;
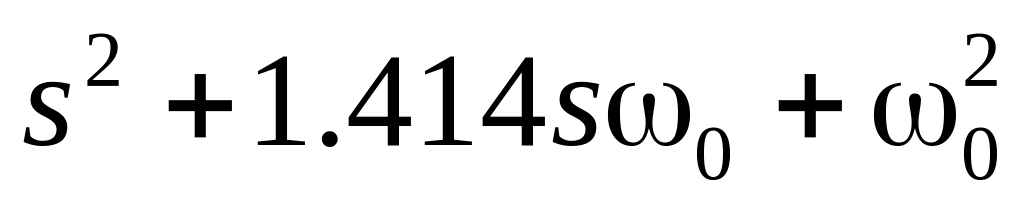 ;
;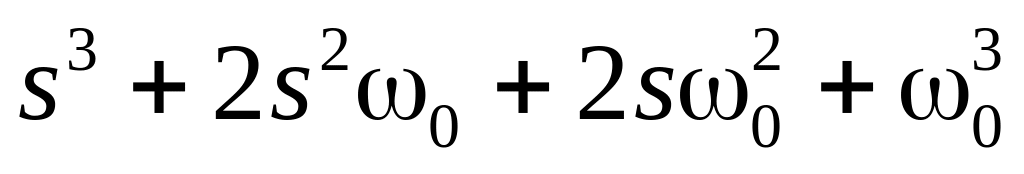 ;
;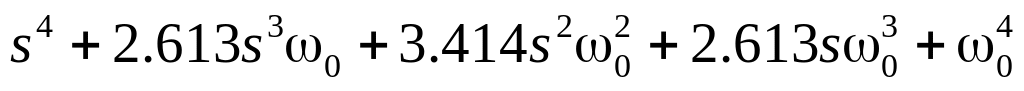 ;
; ;
;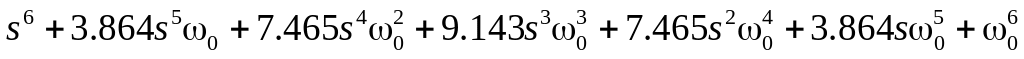 ;
;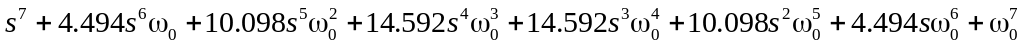 .
.
Маючи передатні функції об'єкта Wo(s)
і бажану Wd(s),
знаходимо неперервну передатну функцію
регулятора Wp(s)
з відомої залежності для замкненої
системи регулювання
![]() .
У математичному застосунку це виглядатиме
таким чином.
.
У математичному застосунку це виглядатиме
таким чином.
MathCAD
|
Потрібно нагадати, що у випадку ПІ- чи ПІД-регулятора параметри передатної функції регулятора вибираються залежно від параметрів об'єкта регулювання, зокрема, зазвичай регулятором компенсуються найбільші сталі часу.
|
Доцільно після синтезу неперервного прототипу регулятора перевірити отриману замкнену неперервну систему і лише після цього приступати до подальшого синтезу цифрового регулятора. У випадку незадовільної роботи неперервного регулятора потрібно провести відповідне налагодження замкненої неперервної системи для отримання бажаної перехідної характеристики і лише після цього переходити до етапу синтезу дискретної системи. |
Наступним етапом є знаходження дискретної
передатної функції за її неперервним
прототипом. Як приклад, для отримання
дискретної передатної функції регулятора
Wpd(z)
застосована проста інженерна
методика з використанням z-форми
![]() .
Потрібно відзначити, що такий метод не
є аналітично точним, тому поведінка
синтезованої системи може відрізнятися
від очікуваної.
.
Потрібно відзначити, що такий метод не
є аналітично точним, тому поведінка
синтезованої системи може відрізнятися
від очікуваної.
MathCAD
|
MATLAB
% Отримання дискретної передатної функції регулятора Wpd = c2d(Wp, 0.05, 'tustin']) |
Аналогічні операції проводяться для об'єкта (знаходиться його дискретна передатна функція Wod(z)) і замкненої системи – дискретна передатна функція Wsd(z).
MathCAD
|
MATLAB
% Отримання дискретної передатної функції об'єкта Wod = c2d(Wo, 0.05, 'tustin']) % Створення замкненої системи W1 = series(Wpd, Wod) % послідовне з'єднання регулятора і об'єкта W = feedback(W1, 1) % замикаємо від'ємний зворотний зв'язок |
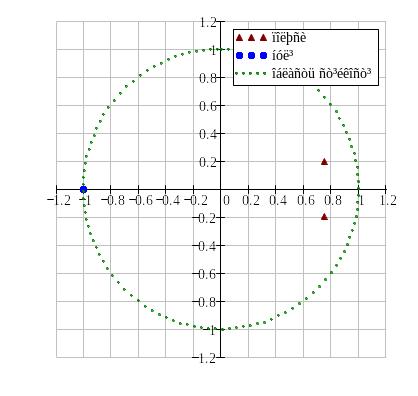
Виконуємо попередній аналіз отриманої замкненої дискретної системи за її передатною функцією. З використанням засобів аналітичної математики MathCAD і засобів MATLAB знаходимо розміщення нулів/полюсів синтезованої замкненої системи (див. нижче).
MathCAD
Характеристичний поліном (знаменник передатної функції)
Коефіцієнти полінома знаменника:
Полюси дискретної передатної функції
Чисельник передатної функції
Коефіцієнти полінома чисельника:
Нулі дискретної передатної функції
Ф
|
MATLAB
% Отримання розподілу нулів/полюсів на комплексній площині % знайденої дискретної замкненої системи pzmap(W), grid |
Знаходження перехідної функції замкненої
дискретної системи з синтезованим
регулятором відбувається шляхом
формування відповідного рекурентного
рівняння для одиничного вхідного сигналу
![]() .
.

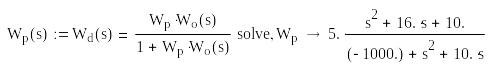
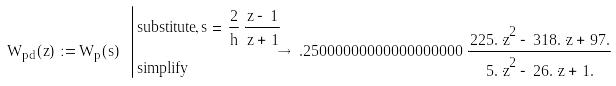
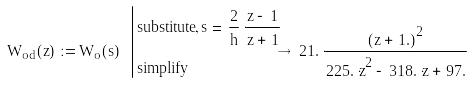
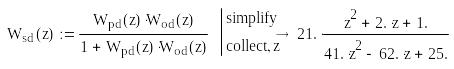
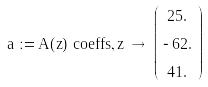
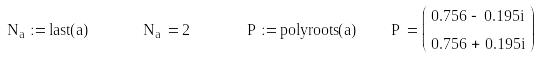
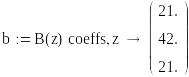
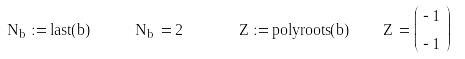
 ормування
одиничного кола (відображення області
стійкості) і виведення графіка
нулів/полюсів
ормування
одиничного кола (відображення області
стійкості) і виведення графіка
нулів/полюсів