Способы определения критической силы

Р асчет по формуле Эйлера

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ 3

ЛЕКЦИЯ 18 3

Основные положения. Гипотезы и допущения 3

ЛЕКЦИЯ 19 3

Тема 2.1. Основные положения. Нагрузки внешние и внутренние, метод сечений 3

Тема 2.2. Растяжение и сжатие. Внутренние силовые факторы, напряжения. Построение эпюр 3

ЛЕКЦИЯ 21 3

Тема 2.2. Растяжение и сжатие. Продольные и поперечные деформации. Закон Гука 3

ЛЕКЦИЯ 23 3

Тема 2.3. Практические расчеты на срез и смятие. Основные предпосылку расчетов и расчетные формулы 3

ЛЕКЦИЯ 26 10

Тема 2.5. Кручение. Внутренние силовые факторы при кручении. Построение эпюр крутящих моментов 10

ЛЕКЦИЯ 27 15

Тема 2.5. Кручение. Напряжения и деформации при кручении 15

ЛЕКЦИЯ 28 3

Тема 2.5. Кручение. Расчеты на прочность и жесткость при кручении 3

ЛЕКЦИЯ 29 7

Тема 2.6. Изгиб. Классификация видов изгиба. Внутренние силовые факторы при изгибе 7

ЛЕКЦИЯ 32 3

Тема 2.6. Изгиб. Нормальные напряжения при изгибе. Расчеты на прочность. 3

ЛЕКЦИЯ 36 3

Тема 2.10. Устойчивость сжатых стержней. Основные положения. 3

J_min -- минимальный осевой момент инерции стержня;

l — длина стержня.

Потеря устойчивости происходит в плоскости наименьшей жесткости, поэтому в формулу входит минимальный из осевых мо­ментов инерции сечения (J_x или J_y).

Формулу распространили на другие формы закрепления стерж­ней, рассмотрев форму потери устойчивости в каждом случае.

Длина стержня заменяется ее приведенным значением, учиты­вающим форму потери устойчивости в каждом случае: l_ПРИВ = μl, где μ — коэффициент приведения длины, зависящий от способа за­крепления стержня (рис. 36.3).

Ф ормула для расчета критической силы для всех случаев

Критические напряжения.

Критическое напряжение — напряжение сжатия, соответству­ющее критической силе.

Напряжение от сжимающей силы определяется по формуле

где σ_кр — напряжение сжатия, при котором стержень еще устойчив. Корень квадратный из отношения минимального момента инерции сечения к площади поперечного сечения принято называть мини­мальным радиусом инерции i_т;_п:

Тогда формула для расчета критического напряжения перепи­шется в виде

Отношение μl/i_min носит название гибкости стержня λ.

Гибкость стержня — величина безразмерная, чем больше гиб­кость, тем меньше напряжение:

Заметим, что гибкость не зависит от материала, а определяется только геометрией стержня.

Пределы применимости формулы Эйлера

Формула Эйлера выполняется только в пределах упругих де­формаций.

Таким образом, критическое напряжение должно быть меньше предела упругости материала.

Предел упругости при расчетах можно заменять пределом про­порциональности. Таким образом, σ_кр ≤ σ_у ≈ σ_пц, где σ_у — предел упругости; σ_ПЦ — предел пропорциональности материала;

Откуда гибкость стержня:

Предельная гибкость зависит от материала стержня.

В случае, если λ < λ_пред в материале стержня возникают оста­точные деформации. Поскольку в реальных конструкциях могут воз­никать пластические деформации, не приводящие к потере работо­способности, созданы эмпирические формулы для расчетов в этих случаях.

Расчет критического напряжения по формуле Ф. О. Ясинского для стальных стержней.

Критическое напряжение определяется по формуле σ_кр = α — bλ, где а и b — коэффициенты, зависящие от материала; их значения представлены в таблице.

Н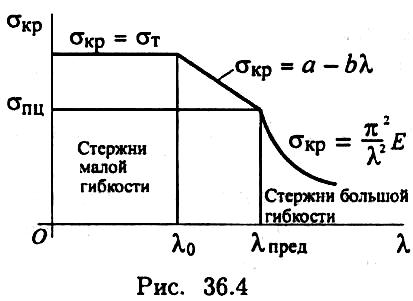 а рис. 36.4 представлена зависимость критического напряже­ния от гибкости стержня.

Для стержней малой гибко­сти проводится расчет на сжатие

.

Для стержней средней гибкости расчет проводят по форму­ле Ясинского σ_кр = α — bλ..

Для стержней большой гибкости расчет проводят по формуле Эйлера

Критическую силу при расчете критического напряжения по формуле Ясинского можно определить как

Условие устойчивости: