Решение

Для данного случая наибольший изгибаю­щий момент возникает посередине пролета

Определяем допускаемое значение наибольшего изги­бающего момента

где

Тогда

Приравниваем вычисленное значение допускаемого изги­бающего момента его значению, выраженному через на­грузку:

откуда

П ример 5. Определить допускаемый изгибающий момент для чугунной балки, сечение которой изображено на рис. 2.60. Допускаемые напряжения на растяжение [σ_р]=300 кгс/см², на сжатие [σ_с] = 800 кгс/см².

Решение

Момент инерции сечения вычисляем как раз­ность моментов инерции большого и малого прямоуголь­ников

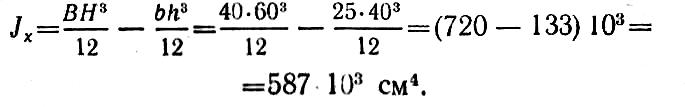
Осевой момент сопротивления

Допускаемый изгибающий момент определяем из расчета по наибольшим растягивающим напряжениям

то же, по наибольшим сжимаю­щим напряжениям

Меньший из вычисленных моментов [М_р] = 58,7 тс-м опре­деляет допускаемую нагрузку балки.

Таким образом, в чугунной балке симметричного сече­ния допускаемая нагрузка ограничивается прочностью растянутых волокон. Чтобы для чугунной балки допускае­мая нагрузка была одинакова по условиям прочности растянутых и сжатых волокон, сечение ее должно быть несимметричным относительно нейтральной оси. Расстоя­ния от нейтральной оси до крайних волокон растянутой зоны у_р и сжатой у_с должны удовлетворять отношению

Этого можно добиться, в частности, применив несимметричный двутавр, у которого горизонтальная полка, находящаяся в растянутой зоне, толще, чем полка, расположенная в сжатой зоне.

Лекция 36 Тема 2.10. Устойчивость сжатых стержней. Основные положения.

Иметь представление об устойчивых и неустойчивых формах равновесия, критической силе и коэффициенте запаса устойчиво­сти, о критическом напряжении, гибкости стержня и предельной гибкости.

Знать условие устойчивости сжатых стержней, формулу Эй­лера и эмпирические формулы для расчета критической силы и кри­тического напряжения.

Понятие об устойчивом и неустойчивом равновесии

Относительно короткие и массивные стержни рассчитывают на сжатие, т. к. они выходят из строя в результате разрушения или оста­точных деформаций. Длинные стержни небольшого поперечного се­чения под действием осевых сжимающих сил изгибаются и теряют равновесие. Такие стержни работают на изгиб и сжатие.

Равновесие считают устойчивым, если за счет сил упругости после снятия внешней отклоняющей силы стержень восстановит первоначальную форму (рис. 36.1).

Если упругое тело после отклонения от равновесно­го положения не возвращается к исходному состоянию, то говорят, что произошла потеря устойчивости, а равновесие было неустойчивым.

Потерю устойчивости под действием центрально приложенной продольной сжимающей силы называют продольным изгибом.

На устойчивость равновесия влияет величина сжимающей силы.

Наибольшее значение сжимающей силы, при которой прямоли­нейная форма стержня сохраняет устойчивость, называют критиче­ской силой. Даже при небольшом превышении критического значе­ния силы стержень недопустимо деформируется и разрушается.

Расчет на устойчивость

Расчет на устойчивость заключается в определении допускаемой сжимающей силы и в сравнении с ней силы действующей:

где F — действующая сжимающая сила;

[F] — допускаемая сжимающая сила, обеспечивает некоторый запас устойчивости;

F_KP — критическая сила;

[s_y] — допускаемый коэффициент запаса устойчивости.

Обычно для сталей [s_у] = 1,8 – 3; для чугуна [s_y] = 5; для дерева [s_у] = 2,8.