Примеры решения задач

Пример 1. Подобрать размеры сечения балки в виде двутавра. Известна схема нагружения балки (рис. 32.9), материал — сталь, допускаемое напряжение материала при изгибе

Решение

1. Для защемленной балки реакции в опоре определять не следует.

Проводим расчеты по характерным точкам. Размеры сечения подбираем из расчета по нормаль­ным напряжениям. Эпюру поперечных сил строить необязательно.

Определяем моменты в характерных точках.

М_А = 0; М_В = F₁• 4; М_в = 20 • 4 = 80 кН • м.

В точке С приложен внешний момент пары, поэтому расчет про­водим для левого сечения (без момента) и для правого — с момен­том т.

Выбираем соответствующий масштаб по максимальному значе­нию изгибающего момента. Опасное сечение — сечение балки, где действует максимальный момент. Подбираем размеры балки в опасном сечении по условию прочности

Основываясь на значении W_x = 500 см³ по таблице ГОСТ 8239-89 выбираем двутавр № 30а: момент сопротивления W_x = 518 см³; площадь сечения А = 49,9 см².

Для сравнения рассчитаем размеры балки квадратного сечения (рис. 32.10) при том же моменте сопротивления сече­ния.

Сторона квадрата Площадь сечения бал­ки А = b² = 14,5² = 210,2 см².

Балка квадратного сечения в 4 раза тяжелее.

Пример 2. Проверить прочность деревянной балки (рис. 2.58), если [σ] = 100 кгс/см²; [т] = 10 кгс/см².

Решение

Максимальные изгибающий момент и попе­речная сила возникают в сечении заделки.

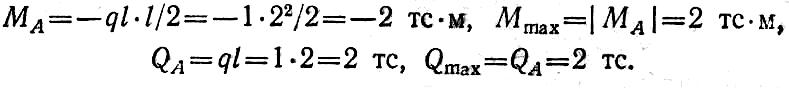
Максимальные нормальные напряжения

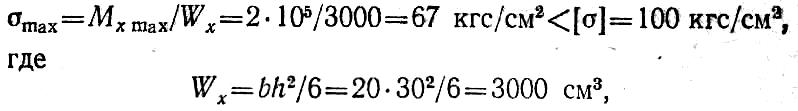
т. е. прочность по нормальным напряжениям обеспечена.

Максимальные касательные напряжения

следовательно, и по касательным напряжения прочность обеспечена.

П ример 3. Подобрать сечение стальной балки, изображенной на рис. 2.59, а в трех вариантах: 1) про­катный двутавр, 2) прямоугольник с отношением сторон h/b = 4/3, 3) круг. Определить отношения масс балок пря­моугольного и круглого сечения к массе балки двутавро­вого сечения. Допускаемое напряжение [σ] = 160 Н/мм². Проверить подобранные сечения по касательным напряже­ниям. Допускаемое касательное напряжение [т] = 96 Н/мм².

Решение

Эпюры поперечных сил и изгибающих момен­тов построены на рис. 2.59,6, в.

М аксимальный изгибающий момент возникает в сече­нии посередине пролета балки М_хтах= 37,5 кН-м. Тре­буемый момент сопротивления

Подбираем сечение балки в трех вариантах:

• Сечение — прокатный двутавр. По таблице ГОСТ 8239—72 подходит двутавровый профиль № 20а, его момент сопротивления W_x = 237 см³, площадь сечения F₁ = 35,5 см²,

• Сечение — прямоугольник с отношением сторон h/b = 4/3.

Для прямоугольника W_x = bh²/6; подставляя сюда b = 3h/4 и приравнивая требуемому значению, получаем:

откуда

Площадь сечения F₂ = 12,3_*9,2 = 113 см².

• Сечение — круг.

откуда

Площадь поперечного сечения

Отношение масс (равное отношению площадей сечений)

Следовательно, балка прямоугольного сечения тяжелее двутавровой в 3,18 раза, а балка круглого сечения — в 3,97 раза.

Проверим прочность балки по касательным напряже­ниям.

Наибольшая поперечная сила

Для двутавра № 20а из ГОСТ 8239—72 находим J_х/S_x = 172 мм, толщина стенки балки b = 0,7 см = 7 мм. Наибольшие касательные напряжения для двутавра

Для прямоугольного сечения h = 123 мм, b = 92 мм

Для круглого сечения d = 134 мм

Во всех случаях максимальные касательные напряже­ния оказались значительно ниже допускаемых.

Пример 4. Определить, какую наибольшую рав­номерно распределенную нагрузку q можно приложить к двухопорной балке пролетом l = 2 м, если ее сечение представляет круг d = 220 мм, а допускаемое напряжение [σ] =100 Н/мм².